Local Search and Optimization Problems

Local Search and Optimization Problems

• The search algorithms we have seen so far, more often concentrate on path through which the goal is reached. But if the problem does not demand the path of the solution and it expects only the final configuration of the solution then we have different types of problem to solve.

• Following are the problems where only solution state configuration is important and not the path which has arrived at solution.

1) 8-queen (where only solution state configuration is expected).

2) Integrated circuit design. 

3) Factory-floor layout.

4) Job-shop scheduling.

5) Automatic programming.

6) Telecommunication network optimization.

7) Vehicle routing.

8) Portfolio management.

If we have such type of problem then we can have another class of algorithms, the algorithms that do not worry about the paths at all. These are local search algorithms.

Local Search Algorithms

- They operate using single state. (rather than multiple paths).

- They generally move to neighbours of the current state.

- There is no such requirement of maintaining paths in memory.

- They are not "Systematic" algorithm procedure.

- The main advantages of local search algorithm are

1) They use very little and constant amount of memory.

2) They have ability to find resonable solution for infinite state spaces (for which systematic algorithms are unsuitable).

Local search algorithms are useful for solving pure optimization problems. In pure optimization problems main aim is to find the best state according to required objective function.

Local search algorithm make use of concept called as state space landscape. This landscape has two structures -

1) Location (defined by the state)

2) Elevation (defined by the value of the heuristic cost function or objective function).

• If elevation corresponds to the cost, then the aim is to find the lowest valley - (a global minimum).

• If elevation corresponds to the objective function then aim is to find the highest peak - (a global maximum).

• Local search algorithms explore the landscape.

Performance measurement

- Local search is complete i.e. it surely finds goal if one exists.

- Local search is optimal as it always find global minimum or maximum.

Local search representation

Hill Climbing Search

• This algorithm generally moves up in the direction of increasing value that is-uphill. It breaks its "moving up loop" when it reaches a "peak" where no neighbour has a higher value.

• It does not maintain a search tree. It stores current node data structure. This node records the state and its objective function value. Algorithm only look out for immediate neighbours of current state.

• It is similar to greedy local search in a sense that it considers a current good neighbour state without thinking ahead.

• Greedy algorithm works very well as it is very easy to improve bad state in hill climbing.

1. Algorithm for Hill Climbing

The algorithm for hill climbing is as follows: -

1) Evaluate the initial state. If it is goal state quit, otherwise make current state as initial state.

2) Select a new operator that could be applied to this state and generate a new state.

3) Evaluate the new state. If this new state is closer to the goal state than current state make the new state as the current state. If it is not better, ignore this state and proceed with the current state.

4) If the current state is goal state or no new operators are available, quit. Otherwise repeat from 2.

2. Problems with Hill Climbing

1) Local maxima - Can't see higher peak.

2) Shoulder - Can't see the way out.

Local maxima- It is a state where we have climbed to the top of the hill, and missed on better solution.

It is the mountain - A state that is better than all of its neighbours, but not better than some other states further away. [Shown in Fig. 4.2.3]

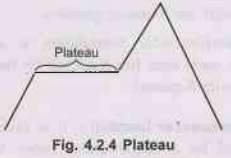
Plateau: It is a state where everything around is about as good as where we are currently. In other words a flat area of the search space in which all neighbouring states have the same value. [Shown in Fig. 4.2.4]

Ridges: In this state we are on a ridge leading up, but we can't directly apply an operator to improve the situation, so we have to apply more than one operator to get there. [Shown in Fig. 4.2.5]

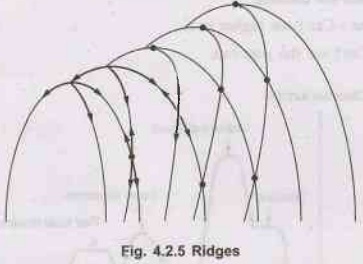
Illustration of ridges: The grid of states (dark circles) is superimposed on a ridge rising from left to right, creating a sequences of local maxima that are not directly connected to each other. From each local maximum all the available actions point downhill.

3. Solving Problems Associated with Hill Climbing

• All the above discussed problems could be solved using methods like backtracking, making big jumps (to handle plateaus or poor local maxima), applying multiple rules before testing (helps with ridges) etc. Hill climbing is best suited to problem where the heuristic gradually improves, the closer it gets to the solution; it works poorly where there are sharp drop-offs. It assumes that local improvement will lead to global improvement.

4. Example for Local Search

Consider the 8-queens problem:

A complete-state formulation is used for local search algorithms. In 8-queens problem, each state has 8-queens on the board one per column. There are two functions related with 8-queens.

1) The successor function: It is function which returns all possible states which are generated by a single queen move to another cell in the same column. The total successor of the each state 8 x 7 = 56.

2) The heuristic cost function: It is a function 'h' which hold the number of attacking pair of queens to each other either directly or indirectly. The value is zero for the global minimum of the function which occurs only at perfect solutions.

5. Advantages of Hill Climbing

- Hill climbing is an optimization technique for solving computationally hard problems.

- It is best used in problems with the property that the" state description itself contains all the information needed for a solution".

- The algorithm is memory efficient since it does not maintain a search tree. It looks only at the current state and immediate future states.

- In contrast with other iterative improvement algorithms, hill-climbing always attempts to make changes that improve the current state. In other words, hill-climbing can only advance if there is a higher point in the adjacent landscape.

- It is often useful when combined with other methods, getting it started right in the as immediate general neighbourhood.

6. Variations of Hill Climbing

Many variants of hill-climbing have been invented as discussed below.

1) Stochastic hill climbing: Chooses at random from among the uphill moves; the probability of selections can vary with the steepness of the uphill move.

2) First choice hill climbing: Implements stochastic hill climbing by generating successors randomly until one is generated that is better than the current state. This is a good strategy when a state has many (e.g. thousands) of successors.

3) Random restart hill climbing: Adopts the well known saying "If at first you don't succeed, try, try again". It conducts a series of hill climbing searches from randomly generated initial states, stopping when a goal is found.

The hill climbing algorithms described so far are incomplete because they often fail to find a goal when surely goal exist. This can happen because these algorithms can get stuck on local maxima. Random restart hill is complete with probability approaching to 1. This algorithm do not stop until it reaches to goal.

The success of hill climbing depends very much on the shape of the state-space landscape. If there are few local maxima and plateaux, random-restart hill climbing will find a good solution very quickly.

4) Steepest ascent hill climbing: This algorithm differs from the basic Hill climbing algorithm by choosing the best successor rather than the first successor that is better. This indicates that it has elements of the breadth first algorithm.

Steepest ascent Hill climbing algorithm

1. Evaluate the initial state.

2. If it is goal state then quit otherwise make the current state this initial state and proceed;

3. Repeat set target to be the state that any successor of the current state can better; for each operator that can be applied to the current state apply the new operator and create a new state evaluate this state.

4. If this state is goal state Then quit. Otherwise compare with Target. If better set Target to this value. If Target is better than current state set current state to Target. Until a solution is found or current state does not change.

Both the basic and this method of hill climbing may fail to find a solution by reaching a state from which no subsequent improvement can be made and this state is not the solution.

Local maximum state is a state which is better than its neighbours but is not better than states faraway. These are often known as foothills. Plateau states are states which have approximately the same value and it is not clear in which direction to move in order to reach the solution. Ridge states are special types of local maximum states. The surrounding area is basically unfriendly and makes it difficult to escape from, in single steps, and so the path peters out when surrounded by ridges. Escape relies on: backtracking to a previous good state and proceed in a completely different direction-involves keeping records of the current path from the outset; making a gigantic leap forward to a different part of the search space perhaps by applying a sensible small step repeatedly, good for plateau; applying more than one rule at a time before testing, good for ridges. None of these escape strategies can guarantee success.

Simulated Annealing Search

1) In simulated annealing, initially the whole space is explored.

2) This is a variation of hill climbing.

3) This avoids the danger of being caught on a plateau or ridge and makes the procedure less sensitive to the starting point.

4) Simulated annealing is done to include a general survey of the scene, to avoid climbing, false foot hills.

5)There are two additional changes -

i) Rather than creating maxima, minimisation is done.

ii) The term objective function is used rather than heuristic.

6) This concept is taken from physical annealing where physical substances are men melted and then gradually cooled until some solid state is reached. In physical annealing the goal is to produce a minimal-energy state. The annealing schedule states, that if the temperature is lowered sufficiently slowly, then the goal will be attained. AE is called the change in the value of the objective function.

7) It becomes clear that in this algorithm we have valley descending rather than hill climbing. The probability that the metal will jump to a higher given by P=exp^8-E/kT where k is Boltzmann's constant.

The algorithm

1) Start with evaluating the initial state.

2) Apply each operator and loop until a goal state is found or till no new operators left to be applied as described below:

i) Set T according to an annealing schedule.

ii) Select and apply a new operator.

iii) Evaluate the new state. If it is a goal state quit.

ΔE = Val (current state) - Val (new state)

• If ΔE < 0 then this is the new current state.

Else find a new current state with probability e - E / KT.

Local Beam Search

1) In the local beam search, instead of single state in the memory k states are kept in the memory.

2) In local beam search states are generated in random fashion.

3) A successor function plays an important role by generating successor of all K states.

4) If any one successor state is goal then no further processing is required.

5) In other case i.e. if goal is not achieved, it observes the K best successors from the list of all successor and process is repeated.

6) At first glance the random parallism is achieved in the sequence by a local beam search with K states.

7) In a random-restart search every single search activity run independently of others.

8) To implement local search, threads are used. The K parallel search threads useful information.

9) The algorithm work on principle of successful successors. If one state generate efficient/goal reaching successor and other K-1 state generate poor successor, then in this situation the successful successors leads all other states.

10) The algorithm drops/leaves the unsuccessful search and concentrate on successful search.

Limitations of local beam search

1) The local beam search has limitation of, lack of variation among the K states.

2) If the state concentrate on small area of state space then search becomes more expensive.

Stochastic Beam Search

1) Its one of the flavour of local beam search, which is very similar to that of stochastic hill climbing.

2) It resolves the limitation of local beam search.

3) Stochastic beam search concentrate on random selection of K successor instead of selecting k best successor from candidate successor.

4) The probability of random selection is increasing function of its success rate.

5) A stochastic beam search is very similar to natural selection, where the child (successor) of a parent state is eugenic (good production) according to its success rate (fitness). Thus the next generation is also very much powerful.

Genetic Algorithms

1) Evolutionary pace of learning algorithm is genetic algorithm. The higher degree of eugency can be achieved with new paradigm of AI called a genetic algorithms.

2) A genetic algorithm is a rich flavour of stochastic beam search.

3) In the genetic algorithm two parent states are combined together by which a good successor state is generated.

4) The analogy to natural selection is the same as in stochastic beam search, except now we are dealing with sexual rather than asexual reproduction.

1. Term used in Genetic Algorithm

1) Population: Population is set of states which are generated randomly.

2) Individual: It is a state or individual and it is represented as string over a finite alphabet.

Example - A string of 0s and 1s.

For example - In 8-queen all states are specified with the position of 8-queens. The memory required is

8×log₂ 8 = 24 bits. Each state is represented with 8 digits.

3) Fitness function: It is a evaluation function. On its basis each state is rated. A fitness function should return higher values for better states. For the state, the probability of being chosen for reproducing is directly proportional to the fitness score.

In 8-queen problem the fitness function has 28 value for number of non attacking pairs.

4) Crossover: Selection of state is dependent on fitness function. If fitness function value is above threshold then only state is selected otherwise discarded. For each state, pairs are divided, that division point or meeting point is called crossover point, which is chosen in random order from the positions in the string.

5) Mutation: Mutation is one of the generic operator. Mutation works on random selections or changes. For example mutation select and changes a single bit of pattern switching 0 to 1 or 1 to #.

6) Schema: The schema is a substring in which position of some bit can be unspecified.

2. Working of a Genetic Algorithm

Input: 1) State population (a set of individuals)

 2) Fitness function (that rates individual).

Steps

1) Create an individual 'X' (parent) by using random selection with fitness function 'A' of 'X'.

2) Create an individual 'Y' (parent) by using random selection with fitness function'B' of 'Y'.

3) Child with good fitness is created for X + Y.

4) For small probability apply mutate operator on child.

5) Add child to new population.

6) The above process is repeated until child (an individual) is not fit as specified by fitness function.

Genetic algorithm example

Example: 8-queens problem states.

States:

Assume each queen has its own column, represent a state by listing a row where the queen is in each column (digits 1 to 8)

For example, the state below will be represented as 16257483.

3. Example: 8 Queens Problem Fitness

Fitness function: Instead of h as before, use the number of non-attacking pairs of queens. There are 28 pairs of different queens, smaller column first, all together, so solutions have fitness 28. (Basically, fitness function is 28 - h)

For example, fitness of the state below is 27 (queens in columns 4 and 7 attack each other).

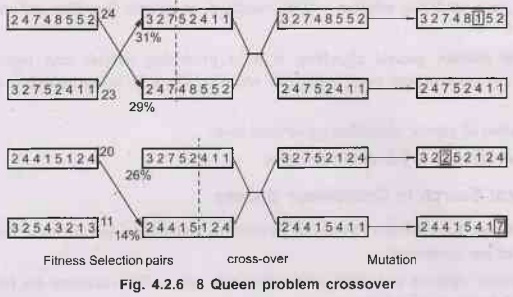
Example: 8 queens problem crossover.

Choose pairs for reproduction (so that those with higher fitness are more likely to be chosen, perhaps multiple times).

For each pair, choose a random crossover point between 1 to 8, say 3.

Produce offspring by taking substring 1-3 from the first parent and 4 - 8 from the second (and vice versa). Apply mutation (with small probability) to the offspring.

Importance of representation

Parts we swap in crossover should result in a well-informed solution (and in addition better be meaningful).

Consider what would happen with binary representation (where position requires 3 digits).

Also chosen representation reduces search space considerably (compared to representing each square for example).

4. Optimization using Genetic Algorithm

1) Genetic algorithm is biological model of intelligent evolution. It generates the population of competing children.

2) The poor candidate solution will be vanished, as genetic algorithm generates best child.

Thus, in practice genetic algorithm is most promising survive and reproduction technique by constructing new optimized solution. Thus it is optimization oriented technique.

Application of genetic algorithm on optimization.

1) Circuit layout. 2) Job-shop scheduling.