Linear Classification Models

Linear Classification Models

• A classification algorithm (Classifier) that makes its classification based on a linear predictor function combining a set of weights with the feature vector.

• A linear classifier does classification decision based on the value of a linear combination of the characteristics. Imagine that the linear classifier will merge into it's weights all the characteristics that define a particular class.

• Linear classifiers can represent a lot of things, but they can't represent everything. The classic example of what they can't represent is the XOR function.

Discriminant Function

• Linear Discriminant Analysis (LDA) is the most commonly used dimensionality reduction technique in supervised learning. Basically, it is a preprocessing step for pattern classification and machine learning applications. LDA is a powerful algorithm that can be used to determine the best separation between two or more classes.

• LDA is a supervised learning algorithm, which means that it requires a labelled training set of data points in order to learn the linear discriminant function.

• The main purpose of LDA is to find the line or plane that best separates data points belonging to different classes. The key idea behind LDA is that the decision boundary should be chosen such that it maximizes the distance between the means of the two classes while simultaneously minimizing the variance within of each class's data or within-class scatter. This criterion is known as the Fisher nib criterion.

• LDA is one of the most widely used machine learning algorithms due to its accuracy and flexibility. LDA can be used for a variety of tasks such as classification, dimensionality reduction, and feature selection.

• Suppose we have two classes and we need to classify them efficiently, then using LDA, classes are divided as follows:

• LDA algorithm works based on the following steps:

a) The first step is to calculate the means and standard deviation of each feature.

b) Within class scatter matrix and between class scatter matrix is calculated

c) These matrices are then used to calculate the eigenvectors and eigenvalues.

d) LDA chooses the k eigenvectors with the largest eigenvalues to form a transformation matrix.

e) LDA uses this transformation matrix to transform the data into a new space with k dimensions.

f) Once the transformation matrix transforms the data into new space with k dimensions, LDA can then be used for classification or dimensionality -reduction

• Benefits of using LDA:

a) LDA is used for classification problems.

b) LDA is a powerful tool for dimensionality reduction.

c) LDA is not susceptible to the "curse of dimensionality" like many other machine learning algorithms.

Logistic Regression

• Logistic regression is a form of regression analysis in which the outcome variable is binary or dichotomous. A statistical method used to model dichotomous or binary outcomes using predictor variables.

• Logistic component: Instead of modeling the outcome, Y, directly, the method models the log odds (Y) using the logistic function.

• Regression component: Methods used to quantify association between an outcome and predictor variables. It could be used to build predictive models as a function of predictors.

• In simple logistic regression, logistic regression with 1 predictor variable.

Logistic Regression:

In[P(Y)/1-P(Y)] = β₀ + β₁ X₁ + β₂ X₂ +...+ β_k X_k

Y = β₀ + β₁ X₁ + β₂ X₂ +...+ β_k X_k + ε

• With logistic regression, the response variable is an indicator of some characteristic, that is, a 0/1 variable. Logistic regression is used to determine whether other measurements are related to the presence of some characteristic, for example, whether certain blood measures are predictive of having a disease.

• İf analysis of covariance can be said to be a t test adjusted for other variables, then logistic regression can be thought of as a chi-square test for homogeneity of proportions adjusted for other variables. While the response variable in a logistic regression is a 0/1 variable, the logistic regression equation, which is a linear equation, does not predict the 0/1 variable itself.

• Fig. 8.4.2 shows Sigmoid curve for logistic regression.

• The linear and logistic probability models are :

Linear Regression :

p = a₀ + a₁ X₁ +a₂ X₂ +...+a_k X_k

Logistic Regression:

In [p/(1-p)] = b₀ +b₁ X₁ +b₂ X₂ +...+b_k X_k

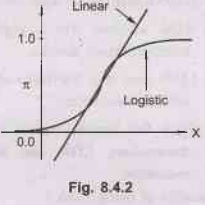
• The linear model assumes that the probability p is a linear function of the regressors, while the logistic model assumes that the natural log of the odds p/(1 - p) is a linear function of the regressors.

• The major advantage of the linear model is its interpretability. In the linear model, if a 1 is 0.05, that means that a one-unit increase in X1 is associated with a 5% point increase in the probability that Y is 1.