Karnaugh Map or K-Map

KARNAUGH MAP OR K-MAP

Boolean functions using Boolean postulates and theorems. It is a time consuming process and re-write the simplified expressions after each step.

To overcome this difficulty, Karnaugh introduced a method for simplification of Boolean functions in an easy way. This method is known as Karnaugh map method or K-map method. It is a graphical method, which consists of 2n cells for 'n' variables. The adjacent cells are differed only in single bit position.

K-Map method is most suitable for minimizing Boolean functions of 2 variables to 5 variables.

2 Variable K-Map

The number of cells in 2 variable K-map is four (22) since the number of variables is two. The following figure shows 2 variable K-Map.

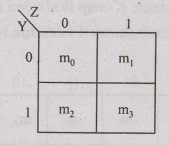
• There is only one possibility of grouping 4 adjacent min terms.

• The possible combinations of grouping 2 adjacent min terms are {(m0, m1), (m2, m3), (m0, m2) and (m1, m3)}.

3 Variable K-Map

The number of cells in 3 variable K-map is eight (23), since the number of variables is three. The following figure shows 3 variable K-Map.

• There is only one possibility of grouping 8 adjacent min terms.

• The possible combinations of grouping 4 adjacent min terms are {(m0, m1, m3, m2), (m4, m5, m7, m6), (m0, m1, m4, m5), (m1, m3, m5, m7), (m3, m2, m7, m6) and (m2, m0, m6, m4)}.

• The possible combinations of grouping 2 adjacent min terms are {(m0, m1), (m1, m3), (m3, m2), (m2, m0), (m4, m5), (m5, m7), (m7, m6), (m6, m4), (m0, m4), (m1, m5), (m3, m7) and (m2, m6)}.

• If x=0, then 3 variable K-map becomes 2 variable K-map.

4 Variable K-Map

The number of cells in 4 variable K-map is sixteen (24), since the number of variables is four. The following figure shows 4 variable K-Map.

• There is only one possibility of grouping 16 adjacent min terms.

• Let R1, R2, R3, and R4, represents the min terms of first row, second row, third row and fourth row respectively. Similarly, C1, C2, C3 and C4 represents the min terms of first column, second column, third column and fourth column respectively. The possible combinations of grouping 8 adjacent min terms are {(R1, R2), (R2, R3), (R3, R4), (R4, R1), (C1, C2), (C2, C3), (C3, C4), (C4, C1)}. If w=0, then 4 variable K-map becomes 3 variable K-map.

5 Variable K-Map

The number of cells in 5 variable K-map is thirty-two (25), since the number of variables is 5. The following figure shows 5 variable K-Map.

• There is only one possibility of grouping 32 adjacent min terms.

• There are two possibilities of grouping 16 adjacent min terms. i.e., grouping of min terms from m0, to m15, and m16 to m31.

• If v=0, then 5 variable K-map becomes 4 variable K-map.

Minimization of Boolean Functions using K-Maps

The combination of inputs for which the Boolean function is '1', then the Boolean function, which is in standard sum of products form after simplifying the K-map.

Similarly, the combination of inputs for which the Boolean function is '0', then the Boolean function, which is in standard product of sums form after simplifying the K-map.

Follow these rules for simplifying K-maps in order to get standard sum of products form.

• Select the respective K-map based on the number of variables present in the Boolean function.

• If the Boolean function is given as sum of min terms form, then place the ones at respective min term cells in the K-map. If the Boolean function is given as sum of products form, then place the ones in all possible cells of K-map for which the given product terms are valid.

• Check for the possibilities of grouping maximum number of adjacent ones. It should be powers of two. Start from highest power of two and upto least power of two. Highest power is equal to the number of variables considered in K-map and least power is zero.

• Each grouping will give either a literal or one product term. It is known as prime implicant. The prime implicant is said to be essential prime implicant, if at least single '1' is not covered with any other groupings but only that grouping covers.

• Note down' all the prime implicants and essential prime implicants. The simplified Boolean function contains all essential prime implicants and only the required prime implicants.

Problem: 70

Reduce the function using K-map F(A,b) = Σ(0,2,3)

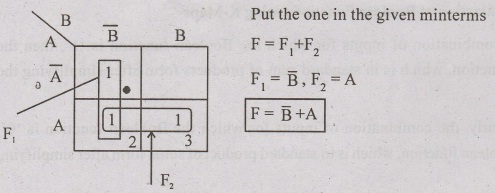
Problem: 71

Simplify the function using Karnaugh Map F(x,y)= Σ(0,1,3)

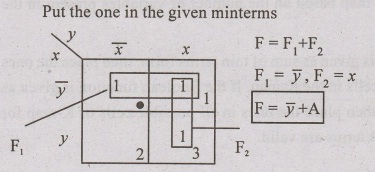
Problem: 72

Reduce the function y(A,B,C) = Σ (0,1,3,6,7)

Solution

Here the 3 variable as in the function so we draw 3 variable k-map and fill ones in the given minterms

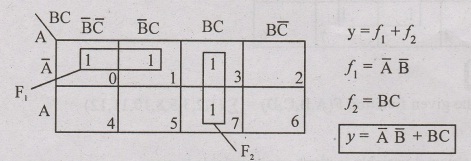
Problem: 73

Reduce the given function y = Σ (4,5,7)

Solution:

Here the 3 variable we use 3 variable k-map and put ones in the k-map

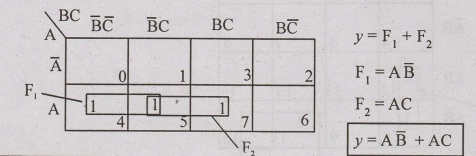
Problems 74

Simplify the sop function F(A,B,C) = Σ (1,2,3,7)

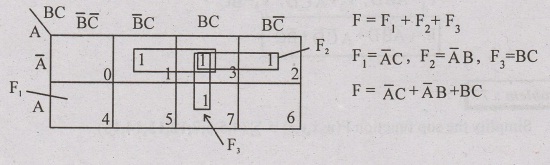
Problem: 75

Simply the sop function F(A,B,C) = Σ (1,3,5,7)

Problem: 76

Reduce the given function F(A,B,C,D) = Σ (1,2,3,5,8,10,11,12)

Solution:

In this problem 4 variable is given use 4 variable k-map

Problem: 77

Simplity the sop function F(w,x,y,z) = Σ (4,5,6,7,12,13,14,15)

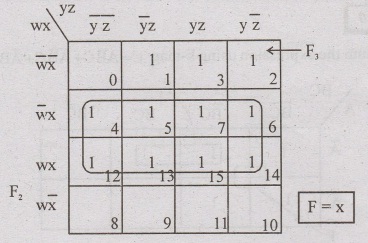
Problem: 78

Simplity the sop function F(A,B,C) = π (0,1,6,7)

Solution:

We use 3 variable and given pos put zero in given terms

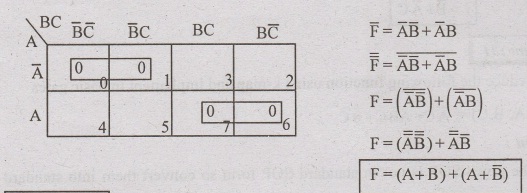
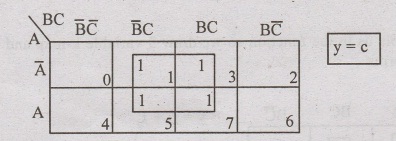
Problem: 79

Simplity the sop function F(x,y,z) = π (0,1,2,3,5,7)

Solution:

We use 3 variable k-map and put zero in the given maxterms

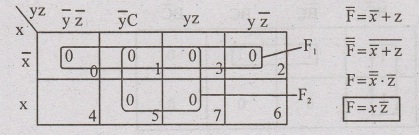
Problem: 80

Minimum the expression using k-map y = ABC+ ABC+AB C+ ABC+ABC

Problem: 81

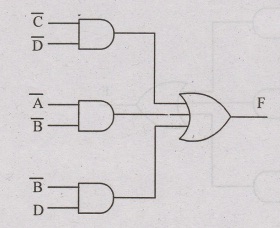
Reduce the following function using k-map and implement in basic gates f(A, B,C) AC+ ABC+BC

Solution :

The given SOP is not in standard SOP form so convert them into standard SOP

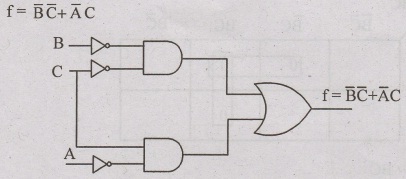
Problem: 82

Reduce the following using karnaugh map f (A, B, C, D) = Σm (0,1,4,8,9,10)

Solution:

Problem: 83

Minimum the expression

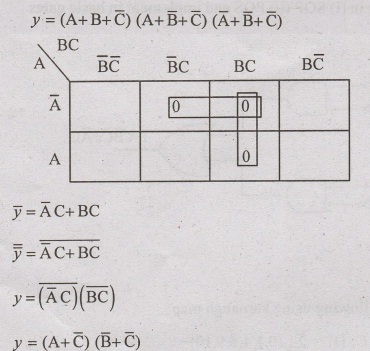
Problem: 84

Minimize the following function f(A,B,C) = π (0,1,3,6,7)

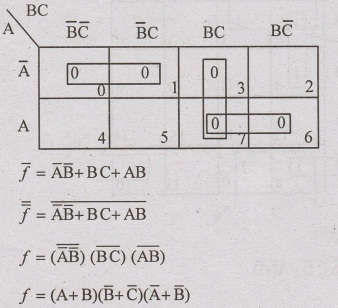
Problem: 85

Simplify the following in (i) SOP (ii) POS and implement in basic gates F(A, B, C, D) = Em(0,1,2,5,8,9,10)

Solution:

(i) SOP put one's in the given numbers

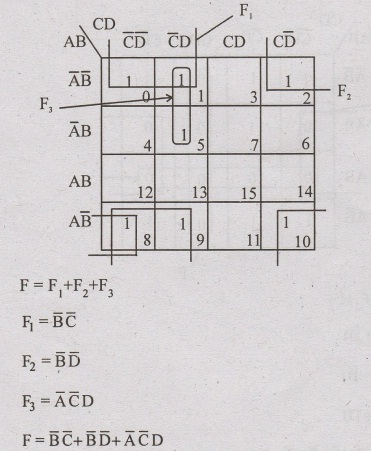
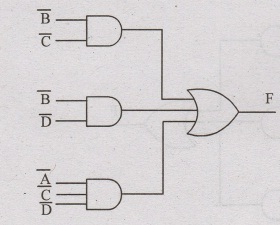
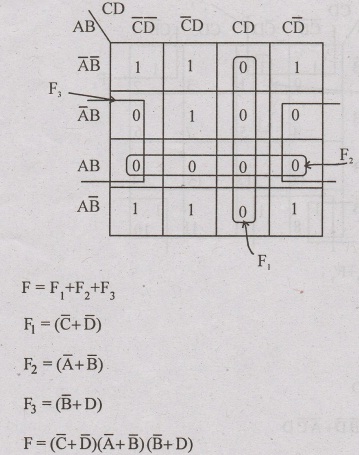
(ii) Product of sum (POS) zero's

Σm (0,1,2,5,8,9,10) π(3,4,6,7,11,12,13,14,15)

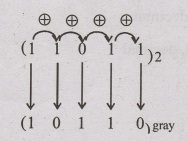
Problem: 86

Convert the given binary code to gray code (11011)2

Solution

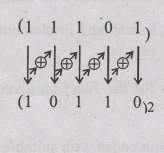
Problem: 87

Convert the gray code to binary (1 1 1 0 1)gray

Solution