Karnaugh Map Minimization

Karnaugh Map Minimization

• During the process of simplification of Boolean expression we have to predict each successive step.

• We can never be absolutely certain that an expression simplified by Boolean algebra alone is the simplest possible expression.

• On the other hand, the map method gives us a systematic approach forsimplifying a Boolean expression.

• The map method, first proposed by Veitch and modified by Karnaugh, hence it is known as the Veitch diagram or the Karnaugh map.

One-Variable,Two-Variable, Three-Variableand Four-Variable Maps

• The basis of this method is a graphical chart known as Karnaugh map (K-map). •

• It contains boxes called cells.

• Each of the cell represents one of the 2n possible products that can be formed from n variables. Thus, a 2-variable map contains = 4 cells, a 3-variable map contains = 8 cells and so forth.

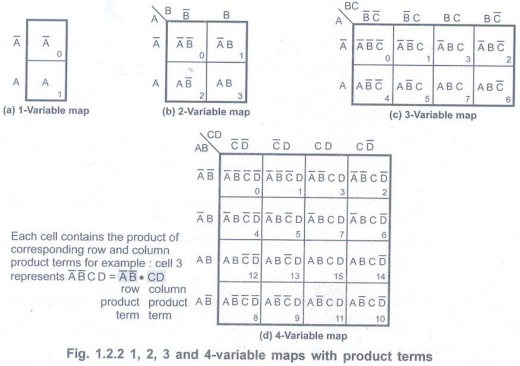
• Fig. 1.2.1 shows outlines of 1, 2, 3 and 4-variable maps.

• Product terms are assigned to the cells of a Karnaugh map by labeling each row and each column of the map with a variable, with its complement, or with a combination of variables and complements.

• The product term corresponding to a given cell is then the product of all variable in the row and column where the cell is located.

• Fig. 1.2.2 shows the way to label the rows and columns of a 1, 2, 3 and 4-variable maps and the product terms corresponding to each cell.

• When we move from one cell to the next along any row or from one cell to the next along any column, one and only one variable in the product term changes (to a complemented or to an uncomplemented form).

• The gray code has same properties (only one variable change when we proceed to next number or previous number) hence gray code is used to label the rows and columns of K-map as shown in Fig. 1.2.3.

• The Fig. 1.2.3 shows label of the rows and columns of a 1, 2, 3 and 4-variable maps using gray code and the product terms corresponding to each cell.

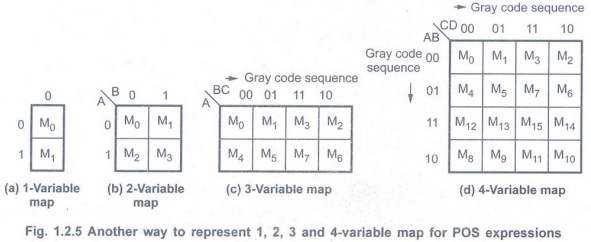
• Instead of writing actual product terms, corresponding shorthand minterm notations are written in the cell and row and columns are marked with gray code instead of variables.

•In case of POS expressions we assign maxterms (sum terms) to the cells of a Karnaugh map.

• The Fig. 1.2.4 shows the way to label the rows and columns of a 1, 2, 3 and 4-variable maps using gray code and the sum terms corresponding to each cell.

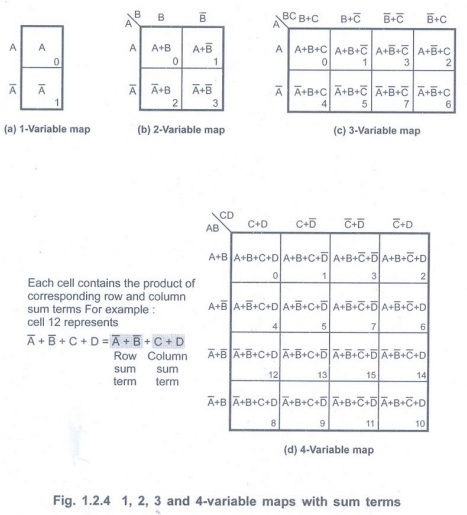
• Instead of writing actual sum terms, corresponding shorthand maxterm notations are written in the cell and row and columns are marked with gray code instead of variables.

Plotting a Karnaugh Map

• Logic function can be represented in various forms such as truth table, SOP Boolean expression and POS Boolean expression. In this section we will see the procedures to plot the given logic function in any form on the Karnaugh map.

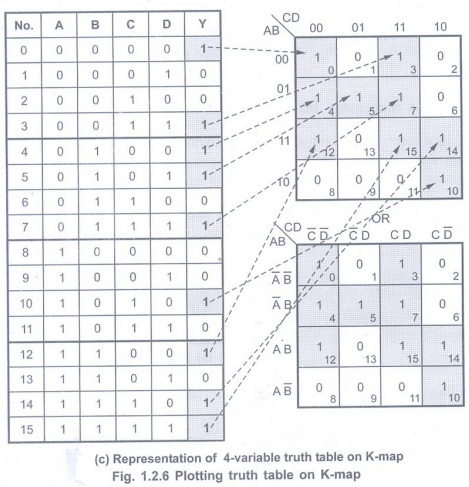
Representation of Truth Table on Karnaugh Map

Cell: The smallest unit of a Karnaugh map, corresponding to one line of a truth table. The input variables are the cell's co-ordinates and the output variable is the cell'scontents.

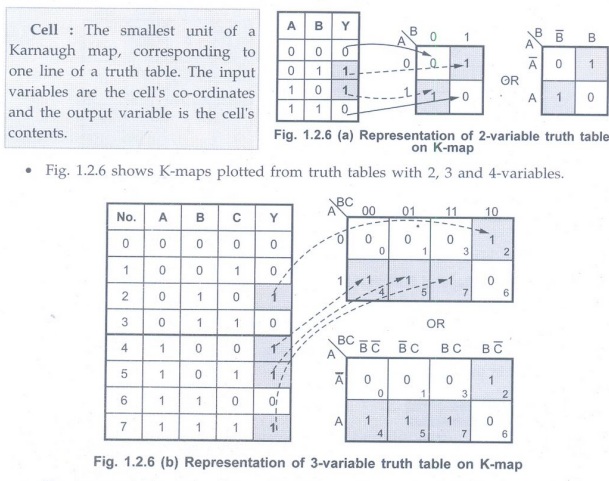
• The terms which are having output 1, have the corresponding cells marked with 1s. The other cells are marked with zeros. (See Fig 1.2.6 (c) on next page)

Note The student can verify the data in each cell by checking the data in the column Y for particular row number and the data in the same cell number in the K-map.

Representing Standard SOP on K-Map

• A Boolean expression in the sum of products form can be plotted on the Karnaugh map by placing a 1 in each cell corresponding to a term (minterm) in the sum of products expression. Remaining cells are filled with zeros. This is illustrated in the following examples.

Examples for Understanding

Example 1.2.1Plot Boolean expression pppppppppppppppon the Karnaugh map.

Representing Standard POS on K-Map

• A Boolean expression in the product of sums can be plotted on the Karnaugh map by placing a 0 in each cell corresponding to a term (maxterm) in the expression. Remaining cells are filled with ones. This is illustrated in the following examples.

Grouping Cells for Simplification

• Once the Boolean function is plotted on the Karnaugh map we have to use grouping technique to simplify the Boolean function.

• The grouping is nothing but combining terms in adjacent cells.

•Two cells are said to be adjacent if they conform the single change rule. i.e. there is only one variable difference between co-ordinates of two cells. For example, the cells for minterms ABC and ĀBC are adjacent.

• The Fig. 1.2.11 shows the adjacent cells. (See Fig. 1.2.11 on next page)

• The simplification is achieved by grouping adjacent 1s or 0s in groups of , where i = 1, 2, ..., n and n is the number of variables.

• When adjacent 1s are grouped then we get result in the sum of products form; otherwise we get result in the product of sums form. Let us see the various grouping rules.

Grouping Two Adjacent Ones (Pair)

• This same principle holds true for any pair of vertically or horizontally adjacent 1s.

• Fig. 1.2.12 (b) shows an example of two vertically adjacent 1s. These two can be combined to eliminate A variable since it appears in both its uncomplemented and complemented forms. This gives result

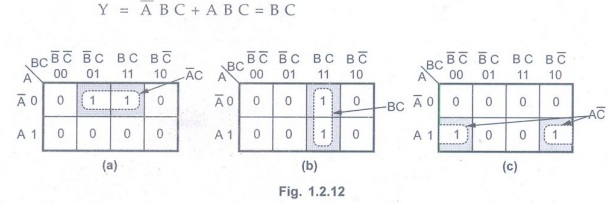
• In a Karnaugh map the corresponding cells in the leftmost column and rightmost column are considered to be adjacent. Thus, the two 1s in these columns with a common row can be combined to eliminate one variable. This is illustrated in Fig. 1.2.12 (c).

Here variable B has appeared in both its complemented and uncomplemented forms and hence eliminated as follows:

A pair is a group of two adjacent cells in a Karnaugh map. It cancels one variable in a K-map simplification.

Grouping Four Adjacent Ones (Quad)

• In a Karnaugh map we can group four adjacent 1s. The resultant group is called Quad. Fig. 1.2.13 shows several examples of quads.

• 1.2.13 (a) shows the four 1s are horizontally adjacent.

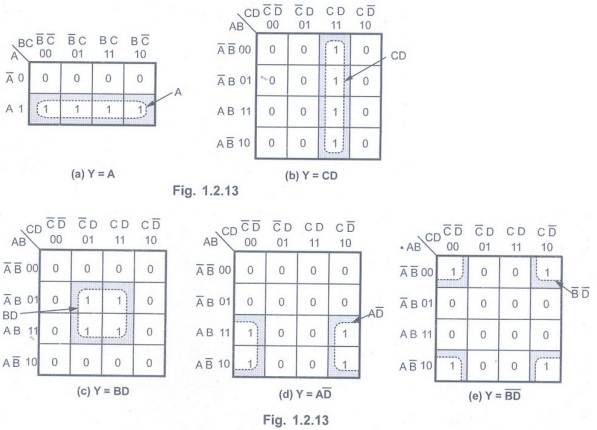
• Fig. 1.2.13 (b) shows the four 1s are vertically adjacent.

• A K-map in Fig. 1.2.13 (c) contains four 1s in a square and they are considered adjacent to each other.

• The four 1s in Fig. 1.2.13 (d) are also adjacent.

• In Fig. 1.2.13 (e) the top and bottom rows are considered to be adjacent to each other and the leftmost and rightmost columns are also adjacent to each other.

• When a quad is combined, two variables are eliminated. For example, in Fig. 1.2.13 (c) we have following terms with 4 variables:

• Fig. 1.2.13(f) shows overlapping groups. As mentioned earlier one term can be shared between two or more groups.

Quad is a group of four adjacent cells in a Karnaugh map. It cancels two variables in a K-map simplification.

Grouping Eight Adjacent Ones (Octet)

• In a Karnaugh map we can group eight adjacent 1s. The resultant group is called as octet. Fig. 1.2.14 shows several examples of octets.

• Fig. 1.2.14 (a) shows the eight 1s are horizontally adjacent.

• Fig. 1.2.14 (b) shows they are vertically adjacent.

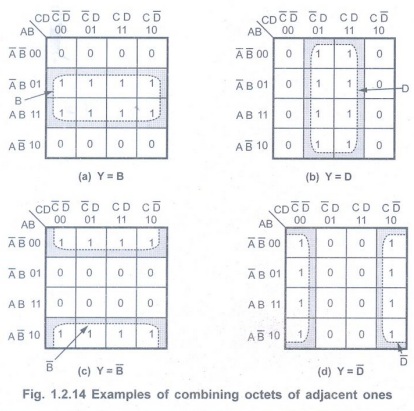
• From the Fig. 1.2.14 we can easily observe that when an octet is combined in a four variable map, three of the four variables are eliminated because only one variable remains unchanged.

• For example, in K-map shown in Fig. 1.2.14 (a) we have following terms:

Octet is a group of eight adjacent cells in a Karnaugh map. It cancels three variables in a K-map simplifications.

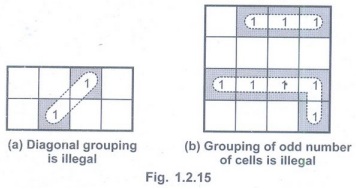
Illegal Grouping

• The Fig. 1.2.15 shows the examples of illegal grouping of cells.