Introduction to Proofs

Introduction to Proofs

1. Direct proofs :

Direct proofs lead from the hypothesis of a theorem to the conclusion. In a direct proof, we assume that P is true and use axioms, definitions, and previous theorems, together with rules of inference, to show that must also be true.

The direct method of proving a conditional P → Q has the following lines of argument.

(i) Hypothesis: First we assume that P is true.

(ii) Analysis: Starting with the hypothesis and employing the rules/laws of logic and other known facts, infer that Q is true.

(iii) Conclusion: P→Q is true.

2. Proof by contraposition

A proof by contraposition is sometimes called an indirect proof. It will make use of the fact that the conditional statement P → Q can be proved by showing that its contrapositive, Q → P is true.

Often in mathematics it is earlier to prove the contrapositive result.

An extremely useful type of indirect proof is known as proof by contraposition.

The indirect methods (conttra position) of proving a conditional P→Q has the following lines of argument.

(i) Hypothesis: P→Q its contrapositive

┐Q → ┐P are logically equivalent.

So assume that ┐Q is true.

(ii) Analysis: Starting with the hypothesis and employing the rules/laws of logic and other known facts, infer that P is true.

(iii) Conclusion: ┐Q → ┐P is true.

3. Vacuous and Trivial proof

It is often used to establish special cases of theorems that state that a conditional statement is true for all positive integers.

We can prove that a quickly a conditional statement P → Q is true when we know that P is false, because P → Q must be true when P is false. Consequently, if we can show that P is false, then we have a proof, called a vacuous proof, of P → Q

4. A little proof strategy:

Here we have described two important approaches for proving theorem of the form ∀x (P(x) → Q (x)): direct proof and proof by contraposition.

Now we use the following lines of arguments.

"We first attempt a direct proof, our attempt is not succeeded we next attempt a proof by contraposition".

5. Proofs by contradiction [Reduction and absurdum]

A proof by contradiction establishes by assuming that the hypothesis P is true and that the conclusion Q is false and then, using P and ┐Q as well as other axioms, definitions and previously derived theorems, derives a contradiction.

The lines of argument in this method of proof of the statement P → Q are as follows

(i) Hypothesis: Assume that P → Q is false. That is, assume that P is true and Q is false.

 (ii) Analysis: Starting with the hypothesis that Q is false and employing the rules of logic and other known facts, infer that P is false. This contradicts the assumption that P is true.

(iii) Conclusion: Because of the contradiction arrived in the analysis, we inferthat P→ Q is true.

6. Proofs of Equivalence

To prove a theorem that is of the form P → Q (biconditional), we show that P → Q and Q → P are both true. The validity of this approach is based on the tautology.

(P ↔ Q) ↔ [(P → Q) ^ (Q → P)]

7. Mistakes in proof

Constructing mathematical proofs there are many common errors occur. Among the most common errors are mistakes in arithmetic and basic algebra.

8. Counter example

To show that a statement of the form ∀x P(x) is false, we need only find a counter example, that is, an example x for which P (x) is false.

Type 1. Problems based on direct proofs

Example 1. Give a direct proof of the statement.

"The square of an odd integer is an odd integer".

Solution: Given: "The square of an odd integer is an odd integer".

i.e., "If n is an odd integer, then n2 is an odd integer".

Let P: n is an odd integer.

Q: n² is an odd integer.

1. Hypothesis: First assume that P is true.

i.e., n is an odd integer is true.

2. Analysis: By the definition of an odd integer.

n = 2k + 1, where k is some integer.

n² = (2k + 1)²

= 4k² + 4k + 1

= 2 (2k² + 2k) + 1

3. Conclusion: We observe that R.H.S value is not divisible by 2.

n² is not divisible by 2.

n² is an odd integer.

i.e., P→Q is true.

Example 2. Give a direct proof of

"The sum of two odd integers is even".

Solution: Given: "The sum of two odd integers is even".

i.e., "If n is odd and m is odd then

n+m is an even integer.

P: 'n' is an odd integer and 'm' is an odd integer.

Q: 'n+m' is an odd integer.

1. Hypothesis: Assume that P is true.

2. Analysis: If n is an odd integer.

then n = 2k + 1 for some integer 'k'.

If m is an odd integer

then m = 2l+1 for some integer 'l'.

n + m = (2k + 1) + (2l+1)

= 2 (k+l+1)

3. Conclusion: We observe that the R.H.S. value is divisible by '2'. This means that n+m is an even integer.

i.e., P→Q is true.

Example 3. Prove that if m+n and n+p are even integers where m, n, p are integers, then m+p is even.

Solution: Given: If m + n is even and n + p is even then m + p is even.

P: m + n is even and n + p is even.

Q: m + p is even.

1. Hypothesis: Assume that P is true.

2. Analysis: If m +n is even then m + n = 2s, for some integer 's

If n + p is even then n + p = 2, for some integer '?'.

m + p = (m + n) + (n + p) - 2n

= 2s + 2t - 2n

= 2 (s + t - n)

3. Conclusion: We observe that R.H.S. value of m + p divisible by 2.

This means that m+p is an even integer.

i.e., P→Q is true.

Example 4. Use a direct proof to show that "every odd integer is the difference of two squares."

Solution: If n is an odd integer then

n = s² – t²

P: n is an odd integer.

Q: n = s² - t²

1. Hypothesis: Assume that P is true.

2. Analysis:

If n is an integer then,

n = 2k + 1, where k is some integer.

n = k² + (2k + 1) − k²

= (k² + 2k + 1) − k²

= (k + 1)² - k²

= s² - t² where s = k + 1, t = k.

3. Conclusion:

We observe that the R.H.S value is the difference of two squares.

P→Q is true.

Type 2. Problems based on "Proof by contraposition".

Example 1. Prove that if n is an integer and 5n+2 is odd, then n is odd.

Solution :

P: n is an integer and 5n+2 is odd.

Q: n is odd.

To prove P→Q is true it is enough to prove ┐Q → ┐P is true.

1. Hypothesis :

Since P→Q its contrapositive.

┐Q → ┐P are logically equivalent.

So assume that is true.

i.e., n is even.

2. Analysis: If n is even, then n = 2k, for some integer k.

5n+2 = 5(2k) +2

= 2 (5k) + 2

=2 (5k + 1)

3. Conclusion :

We observe that R.H.S value of 5n+ 2 is divisible by 2.

This means that 5n+2 is an even integer.

i.e., P is true.

┐Q → ┐P is true.

Example 2. Show that if n is an integer and n3 +5 is odd, then n is even using a proof by contraposition.

Solution : P: n is an integer and n3 + 5 is odd.

Q: n is even

To prove PQ is true, it is enough to prove that ┐Q → ┐P is true.

1. Hypothesis:

Since P → Q its contrapositive ┐Q → ┐P are logically equivalent.

So assume that ┐Q is true.

i.e., n is odd.

2. Analysis: If n is odd then n = 2k + 1 for some integer k.

n³ + 5 = (2k + 1)³ + 5

= 8k³ + 12k² + 6k + 1 + 5

= 8k³ + 12k² + 6k + 6

= 2 (4k³ + 6k² + 3k+3)

3. Conclusion: We observe that R.H.S value of n³ + 5 is divisible by 2.

This means that n³ +5 is an even integer.

i.e., ┐P is true.

i.e., ┐Q → ┐P is true.

Type 3. Problem based on VACUOUS and TRIVIAL PROOFS

Example: Show that the proposition P(O) is true, where P (n) is "If n > 1, then n² > n" and the domain consists of all integers. What kind off proof did you use.?

Solution: We use vacuous proof.

P: n > 1

Q: n² > n

P→Q is true.

To show that P is false.

Here n > 1, but 0> 1 is false.

P (0) is "If 0 > 1, then 0² > 0"

This tells us P (0) is automatically true.

Type 4. Problem based on contradiction

Example 1. Provide a proof by contradiction of the following statement "For every integer n, if n² is odd, then n is odd".

Solution:

P: For every integer n, if n² is odd.

Q: n is odd.

1. Hypothesis: Assume that P→Q is false.

i.e., Assume that P is true and Q is false.

i.e., n is not odd ⇒ n is even.

2. Analysis: If n is even then n = 2k for some integer k.

n² = (2k)² = 4k²

3. Conclusion: We conclude that R.H.S of n² is divisible by 2.

This means that n² is even.

This contradicts the assumption P is true.

In view of this contradiction, we infer that the given conditional P→Q is true.

Example 2. Give a proof by contradiction of the theorem "If 3n+2 is odd, then n is odd".

Solution :

P: 3n+2 is odd

Q: n is odd.

1. Hypothesis: Assume that P → Q is false.

i.e., Assume that P is true and Q is false.

i.e., n is not odd ⇒ n is even.

2. Analysis: If n is even then n = 2k, for some integer k.

3n+ 2 = 3 (2k) +2

= 6k + 2

= 2(3k+1)

3. Conclusion: We observe that the R.H.S value of 3n + 2 is divisible by 2.

This means that 3n+ 2 is even.

This contradicts the assumption P is true.

In view of this contradiction, we infer that the given conditional P→Q is true.

Example 3. Prove that if 1/x is irrational.

Solution :

P: x is irrational.

Q: is irrational.

1. Hypothesis: Assume that P → Q is false.

That is, assume that P is true and Q is false.

i.e., 1/x is not irrational ⇒1/x is rational.

2. Analysis: 1/x is rational.

⇒ 1/x = p/q, q ≠ 0 [If p = 0,1 = (0) (x) with is absurd]

⇒ 1/x = cannot be zero.

⇒ x = 1/(1/x) = 1/(p/q) = p/q           (p ≠ 0)

3. Conclusion: Thus by definition x is rational. This contradicts our assumption P is true.

From this we get P → Q is true.

Type 5. Problem based on EQUIVALENCE

Example: Prove that "If n is a positive integer, then n is odd if and only if n² is odd.".

Solution : P: n is a positive integer and n is odd

Q: n² is odd.

To prove P → Q is true and Q → P is true.

 (i) First we prove P → Q is true by direct method.

See Example 1 in type 1.

(ii) To prove Q→ P is true.

See Example 1 in type 4.

Type 6. Problem based on mistakes in proofs

Example: What is wrong with this famous proof 1 = 2?

Let a = b …..(1)

(1) × a ⇒    a² = ab …..(2)

a² - b² = ab - b² …..(3)

= (a - b) (a + b) = b (a - b) ……(4)

(4)/a-b ⇒ a+b = b ……(5)

b + b = b ……(6) by (1)

2b = b ……(7)

(7)/b ⇒ 2 = 1

Solution: The error is that a - b equals zero; division of both sides of an equation by the same quantity is valid as long as this quantity is not zero.

Type 7. Counter example type problems

Example 1. Let A be any 2 x 2 matrix. Prove or disprove that (A = A²) A = 0 or A = I (i.e., A is a null matrix or a unit matrix).

Solution: Consider the counter example :

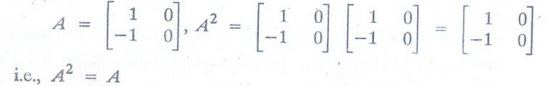
But A ≠ 0 and A ≠ I

Hence the result is disproved.

Example 2. Prove or disprove the result

(∀x ϵ z) [x² - 2x = x - 2], Z = set of integers.

Solution: Consider the counter example,

x = 4, we have

L.H.S x² - 2x = 4² – 8 = 16 - 8 = 8

R.H.S= x - 2 = 4 - 2 = 2

Now L.H.S ≠ R.H.S.

This counter example disproves the result.

EXERCISES

1. Show that the square of an even number is an even number using a direct proof.

 [Ans. Suppose that n is even. Then n = 2k for some integer k. ⇒ n² = (2k)² = 4k² = 2 (2k²). Since we have written n² as 2 times an integer, we conclude that n² is even.

2. Prove or disprove that the product of two irrational numbers in irrational.

[Ans. Since √2.√2 = 2 is rational and √2 is irrational, the product of two irrational numbers is not neccesarily irrational.

3. Use a proof by contraposition to show that if x + y ≥ 2, where x and y are real numbers, then x ≥ 1 or y ≥ 1

[Ans. Assume that it is not true that x ≥ 1 or y ≥ 1. Then x < 1 and y < 1. Adding these two inequalities, we obtain x + y < 2, which is the negation of x + y ≥ 2].

4. Let P (n) be the proposition "If a and b are positive real numbers, then (a + b)ⁿ ≥ aⁿ +bⁿ." Prove that P (1) is true. What kind of proof did you use?

[Ans. P (1) is true because (a + b)¹ = a + b ≥ a¹ +b¹ = a + b. Direct proof].

5. Show that at least 10 of any 64 days chosen must fall on the same day of the week.

[Ans. If we chose 9 or fewer days on each day of the week, this would account for at most 9.7 = 63 days. But we chose 64 days. This contraction shows that at least 10 of the days we chose must be on the same day of the week].

6. Prove that if n is a positive integer, then n is odd if and only if 5n+6 is odd.

 [Ans. First, assume that if n is odd, then n = 2k + 1 for some integer k. ⇒ 5n + 6 = 5 (2k + 1) + 6 = 10 + 11 = 2 (5k+5) + 1. Hence, 5n+6 is odd. To prove the converse, suppose that n is even, so that n = 2k for some integer k. Then 5n+6= 10 + 6 = 2 (5k+3), so 5n+6 is even. Hence, n is odd if and only if 5n+ 6 is odd]

7. Prove or disprove that if m and n are integers such that mn = 1, then either m = 1 and n = 1, or else m = -1 and n = -1.

[Ans. This proposition is true. If m is neither 1 nor -1. Then mn has a factor m larger than 1. On the other hand, mn = 1, and 1 has no such factor. Hence, m = 1 or m = -1. In the first case n = 1 and in the second case n = -1, since n = 1/m

8. Show that these statements about the integer x are equivalent : (i) 3x + 2 is even, (ii) x + 5 is odd.

 [Ans. We prove that all these are equivalent to x being even. If x is even, then x = 2k for some integer k. Therefore 3x + 2=3. 2k + 2 = 6k+2 = 2 (3k+1), which is even, because it has been written in the form 2t, where t = 3k+1. Similarly, x + 5 = 2k + 5 = 2k + 4 + 1 = 2 (k + 2) + 1, so x + 5 is odd].

9. What is wrong with this proof?

Theorem: If n² is positive, then n is positive.

Proof: Suppose that n² is positive. Because the conditional statement "If n is positive, then n² is positive" is true. We can conclude that n is positive.

10. Show that the statement "Every positive integer is the sum of the squares of two integers". is false.

11. Show that these statements about the integer n are equivalent.

P₁: n is even

P₂: n-1 is odd

P₃: n² is even.

12. Prove that √2 is irrational by giving a proof by contradiction.

13. Show that atleast four of any 22 days must fall on the same day of the week.

14. Let P(n) be "If a and b are positive integers with a ≥b, then aⁿ≥bⁿ", where the domain consists of all integers. Show that P (0) is true.

15. Prove that if n = ab, where a and b are positive integers, then a ≤ √n or b ≤ √n.

16. Give a direct proof that if m and n are both perfect squares, then nm is also a perfect square."