Infix to Postfix Conversion

Infix to Postfix Conversion

Algorithm                                            

Read an expression from left to right each character one by one

1. If an operand is encountered then add it to postfix array.

2. If '(' is read, then simply push it onto the stack. Because the (has highest priority when read as an input.

3. If ')' is reads, then pop all the operands until (is read. Discard (. Store the popped characters in the postfix array.

4. If operator is read then

i) If instack operator has greatest precedence (or equal to) over the incoming operator then pop the operator and add it to postfix expression. Repeat this step until we get the instack operator of higher priority than the current incoming operator. Finally push the incoming operator onto the stack.

ii)  Else push the operator.

5. The postfix expression in in array.

The priorities of different operators when they are in stack will be called instack operators and the priorities of different operator when they are read from input will be called as incoming priorities. These priorities are as given below -

Ex. 2.7.1: A * B + C $. Obtain postfix expression.

Sol. :

Ex. 2.7.2 Obtain the postfix expression for (A+B)*(C-D)$.

Sol. :

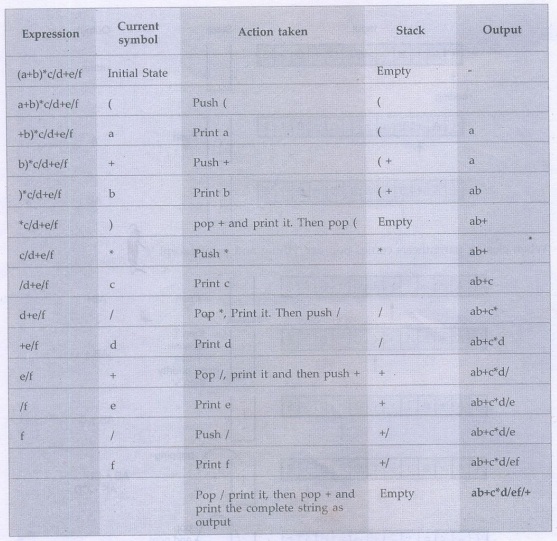
Ex. 2.7.3:  Write an algorithm to convert an infix to postfix expression Trace the algorithm to convert the infix expression "(a+b)*c/d+elf" to a postifx expression. Explain the need for infix and postfix expressions.

Sol. :

The infix expressions are used in mathematical expressions and postfix expressions are used in compilers for checking the syntax of an expression. The postfix expressions are also used in evaluating the expressions.

Ex. 2.7.4 : Convert the following infix expression to the postfix expression. Show stack traces. i) A/B$C+D*E/F-G+H (ii) (A+B)*D+E/(F+G*D)+C.

Sol. : i)

ii)

Ex. 2.7.5: Show the simulation using stack for the following expression to convert infix to postfix: p*q+ (r-s/t)

Solution Consider expression p* q + (r-s/t)

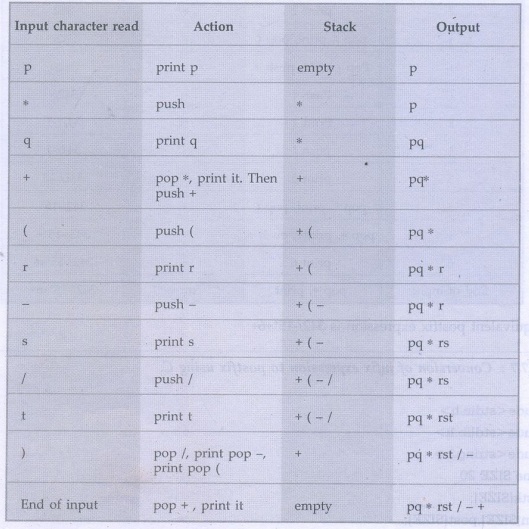
The postfix expression is pq*rst/-+

Ex. 2.7.6 Simulate the conversion of infix to postfix expression using stack for the following expression : 3-(4/2)+(1*5)+6.

Sol. :

The equivalent postfix expression is 342/-15*+6+

Ex. 2.7.7 Conversion of infix expression to postfix using C.

#include<stdio.h>

#include<stdlib.h>

#include<string.h>

#define SIZE 20

char stk[SIZE];

char in [SIZE],post [SIZE];

int top= -1;

void push(char item)

{

top++;

stk[top] = item;

}

char pop()

{

char temp;

temp = stk[top];

top--;

return temp;

}

int stempty()

{

if(top==-1)

return 1;

else

return 0;

}

void inTopost();

int precedence(char);

int main()

{

printf("Enter the infix expression: ");

gets(in);

inTopost();

return 0;

}

int precedence (char ch)//highest num-highest priority

{

switch(ch)

{

case '^':

return 3;

case '/':

case '*;

return 2;

case '+':

case '-':

return 1;

default: return 0;

}

}

void inTopost()

{

int i,j=0;

char ch,next_ch;

for(i=0;i<strlen(in);i++)

{

ch= in[i];

switch(ch)

{

case '(': push(ch);

break;

case ')': while((next_ch=pop())!='(')

post [j++]=next_ch;

break;

case '+':

case '-':

case '*':

case '/':

case '^': while (!stempty()&&(precedence (stk[top])>=precedence(ch)))

post [j++]=pop();

push(ch);//else part

break;

default:post [j++]=ch;//if operand is encountered simply add it to postfix

}

}

while(!stempty())

post[j++]=pop();

post [j]='\0';

for(i=0;i<strlen(post);i++)

printf("%c",post[i]);

}

Output

Enter the infix expression: (a+b)* (c-d)

ab+cd-*