Inclusion and Exclusion - Applications of Inclusion and Exclusion

Inclusion and Exclusion - Applications of Inclusion and Exclusion

Principle of Inclusion and Exclusion

Let X and Y be two finite subsets of a universal set U. If X and Y are disjoint, then

|XUY| =│X│∩+ │Y│

If X and Y are not disjoint then

|XUY| =│X | + | Y | - | X∩Y |

This is called the principle of inclusion and exclusion.

Example 1. Give a formula for the number of elements in the union of four sets.

Solution: By the principle of inclusion and exclusion we get

Example 2. Find a formula for the probability of the union of five events in a sample space if no four of them can occur at the same time.

Solution :

Theorem: If X₁, X₂, … X_n be finite sets, then

Example 3. A total of 1232 students have taken a course in Tamil, 879 have taken a course in English and 114 have taken a course in Telugu. Further, 103 have taken courses in both Tamil and English, 23 have taken courses in both Tamil and Telugu and 14 have taken courses in both English and Telugu. If 2092 students have taken at least one of Tamil, English and Telugu, how many students have taken a course in all three languages?

Solution: Let T→ students who have taken a course in Tamil.

E → students who have taken a course in English.

R → students who have taken a course in Telugu.

i.e., |T| = 1232,   |E| = 879, |R| = 144

|T∩E| = 103, |E∩R| = 23, |E∩R| = 14

and |T U E U R| = 2092

by the principle of inclusion and exclusion we get

|T U E U R | = |T| + |E| + |R| - |T∩E | - |T∩R| - |E∩R| + |T ∩ E ∩ R |

⇒ 2092 = 1232 + 879 + 114 – 103 – 23 – 14 + |T ∩ E ∩ R|

⇒ |T ∩ E ∩ R |= 7

Therefore, there are seven students who have taken courses in Tamil, English and Telugu.

Example 4. Find a formula for the probability of the union of n events in a sample space.

Solution: The probability of the union of n events in a sample. space is

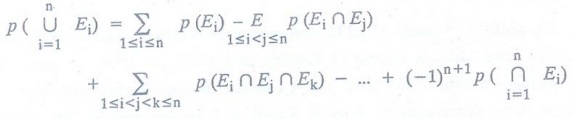
Example 5. Write out the explicit formula given by the principle of inclusion-exclusion for the number of elements in the union of five sets.

Solution :

Example 6. Find the number of positive integers not exceeding 100. that are not divisible by 7 or by 11.

Solution: Let A be the set of positive integers not exceeding 100 that are divisible by 7.

Let B be the set of positive integers not exceeding 100 that are divisible by 11.

Then AUB is the set of positive integers not exceeding 100 that are divisible by either 7 or 11 and A∩B is the set of positive integers not exceeding 100 that are divisible by both 7 and 11.

We know that among the positive integers not exceeding 100 there are [100/7] integers divisible by 7 and [100/11] integers divisible by 11.

Since 7 and 11 are relatively prime, the integers divisible by both 7 and 11 are those divisible by (7) (11).

There are 100 / (7)(11) positive integers not exceeding 100 that are divisible by both 7 and 11.

|AUB| = |A| + |B| - |A∩B|

= [100/7] + [100/11] – [100 / (7)(11)]

= 14 + 9 - 1 = 22

Example 7. Among the first 1000 positive integers : Determine the integers which are not divisible by 5, nor by 7, nor by 9.

Solution: Let A be the number of integers divisible by 5

B be the number of integers divisible by 7.

C be the number of integers divisible by 9.

The number of integers divisible by 5, 7 and 9.

|A U B U C| = 200 + 142 + 111 – 28 – 22 - 15 + 3

= 391

The number of integers not divisible by 5, nor by 7, nor by 9.

= Total number of integers - integers divisible by 5, 7 and 9

= 1000 - 391 = 609

Example 8. In a survey of 300 students, 64 had taken a Mathematics course, 94 had taken a English course, 58 had taken a Computer course, 28 had taken both a Mathematics and a Computer course, 26 had taken both a English and Mathematics course, 22 had taken both a English and a Computer course, 14 had taken all three courses. How many students were surveyed who had taken non of the three courses?

Solution: Given: |M| = 64; |Ε| = 94; |C| = 58

|M∩C| = 28; |M∩E| = 26; |E∩C| = 22

|M∩E∩C| = 14

|MUEUC| = |M| + |E| + |C| - |M∩C | - |M∩E| - |E∩C| + |M∩E∩C|

= 64 + 94 + 58 – 28 - 22 + 14 = 154

Students who had taken none of the courses

= 300 - 154 = 146

Example 9. How many solutions does x₁ + x₂ + x₃ =13 have, where X₁, X₂ and X₃ are non-negative integers with x₁ < 6, x₂ < 6 and X₃ < 6?

Solution: To apply the principle of inclusion - exclusion, let a solution have property P₁ if x₁ ≥ 6, property P₂ if x₂ ≥ 6, and property P₃ if x₃ ≥ 6. The number of solutions satisfying the inequalities x₁ < 6, x₂ < 6 and x₃ < 6 is

N (P₁' P₂' P₃') = N - N(P₁) - N(P₂) - N(P₃) + N(P₁ P₂) + N(P₁ P₃) + N(P₂ P₃) - N(P₁P₂P₃) ….(1)

N = total number of solutions = C (3 + 13 - 1, 13) = C (15, 13) = 105

N(P₁) = (number of solutions with x₁ ≥ 6) = C(3+7-1,7) = 36

N(P₂) = (number of solutions with x₂ ≥ 6) = C (3+7-1,7) = C(9,7) = 36

N(P₃) = (number of solutions with x₃ ≥ 6) = C (3+7-1,7) = C (9,7) = 36

N(P₁P₂) = (number of solutions with x₁ ≥ 6 and x₂ ≥ 6) = C (3 + 1 - 1, 1) = 3

N (P₁P₃) = (number of solutions with x₁ ≥ 6 and x₂ ≥ 6) = C (3 + 1- 1, 1) = 3

N (P₂P₃) = (number of solutions with x₂ ≥ 6 and x₃ ≥ 6) = C (3 + 1 - 1, 1) = 3

N (P₁P₂P₃) = (number of solutions with x₁ ≥ 6, x₂ ≥ 6 and x₃ ≥ 6) = 0

Inserting these quantities into the formula for N (P₁' P₂' P₃') shows that the number of solutions with x₁ ≤ 6, x₂ ≤ 6 and x₃ ≤ 6 equals

(1) ⇒ N (P₁' P₂' P₃') = 105 – 36 – 36 - 36 + 3 + 3 + 3 – 0 = 6

Theorem: Let m and n be positive integers with m ≥ n. Then, there are n^m -C(n,1)(n−1)^m + C(n,2) (n-2)^m-... +(-1)^n-1 C(n,n-1).1^m  onto functions from a set with m elements to a set with n elements.

Proof: There are n^m functions from a set with m elements to a set with n elements,

⇒ C (n, 1) (n - 1)^m functions from a set with m elements to a set with n elements that loose exactly one elements.

⇒ C (n, 2) (n - 2)^m functions from a set with m elements to a set with n elements that loose exactly two elements, and so on.

⇒ C (n, n-1), 1^m functions from a set with m elements to a set with n elements that loose exactly n - 1 elements.

Hence, by inclusion - exclusion principle there are

n^m - C(n, 1) (n - 1)^m + C (n, 2) (n − 2)^m -…. +(-1)^n-1 C (n, n - 1), 1^m onto functions.

Theorem: The number of derrangements of a set with n elements is

D_n =n! [ 1 – 1/1! + 1/2! – 1/3! + ….+ (-1)ⁿ 1/n]

EXERCISE 2.9

1. A survey of households in the United States reveals that 96% have at least one television set, 98% have telephone services, and 95% have telephone service and at least one television set. What percentage of households in the Union States have neither telephone service nor a television set? [Ans. 1%]

2. How many elements are in A₁U A₂ if there are 12 elements in A₁, 18 elements in A₂, and

(a) |A₁∩A₂| = 1?

(b) |A₁∩A₂| = 6?

 [Ans. (a) 29, 24]

3. Find the number of elements in A₁UA₂ UA₃ if there are 100 elements in each set and if

(a) the set are pairwise disjoint. [Ans. 300]

(b) there are 50 common elements in each pair of sets and no elements in all three sets. [Ans. 150]

(c) the sets are equal. [Ans. 100]

4. There are 2504 computer science students at a school. Of these, 1876 have taken a course in Pascal, 999 have taken a course in Fortran, and 345 have taken a course in C. Further, 876 have taken courses in both Pascal and Fortran, 231 have taken courses in both Fortran and C, and 290 have taken courses in both Pascal and C. If 189 of these students have taken courses in Fortran, Pascal, and C, how many of these 2504 students have not taken a course in any of these three programming languages?    [Ans. 492]

5. How many students are enrolled in a course either in calculus, discrete mathematics, data structures, or programming languages at a school if there are 507, 292, 312, and 344 students in these courses, respectively; 14 in both calculus and data structures; 213 in both calculus and programming languages; 211 in both discrete mathematics and data structures; 43 in both discrete mathematics and programming languages; and no student may take calculus and discrete mathematics, or data structures and programming languages, concurrently?  [Ans. 974]

6. How many elements are in the union of four sets if the sets have 50, 60, 70 and 80 elements, respectively, each pair of the sets has 5 elements in common, each triple of the sets has 1 common element, and no element is in all four sets?   [Ans. 234]

7. Find the number of positive integers not exceeding 100 that are either odd or the square of an integer.    [Ans. 55]

8. How many permutations of the 10 digits either begin with the 3 digits 987, contain the digits 45 in the fifth and sixth positions, or end with the 3 digits 123?   [Ans. 50, 138]

9. How many bit strings of length eight do not contain six consecutive 0s?    [Ans. 248]

10. Find the probability that when four numbers from 1 to 100, inclusive, are picked at random with no repetitions allowed, either all are odd, all are divisible by 3, or all are divisible by 5.     [Ans. 4972/71,295]

11. Suppose that in a bushel of 100 apples there are 20 that have worms in them and 15 that have bruises. Only those apples with neither worms nor bruises can be sold. If there are 10 bruised apples that have worms in them, how many of the 100 apples can be sold?        [Ans. 75]

12. How many solutions does the equation x₁ + x₂ + x₃ = 13 have where x₁, x₂ and x₃ are non-negative integers less than 6?          [Ans. 6]

13. How many positive integers less than 10,000 are not the second or higher power of an integer?       [Ans. 9875]

14. Find the number of primes less than 200 using the principle of inclusion-exclusion.       [Ans. 46]

15. How many ways are there to distribute six different toys to three different children such that each child gets at least one toy?        [Ans. 540]

16. How many derangements are there of a set with seven elements?   [Ans. 1854]

17. In how many ways can seven different jobs be assigned to four different employees so that each employee assigned at least one job and the most difficult job is assigned to teh best employee?     [Ans. 2100]

18. How many ways can the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 be arranged so that no even digit is in its original position?      [Ans. 2,170,680]