Higher Order and Directional Consistency

Higher Order and Directional Consistency

Arc consistency

• There have been many advances in how constraint solvers search for solutions. We look first at a pre-processing step which can greatly improve efficiency by pruning the search space, namely arc-consistency. Following this, we'll look at two search methods, backtracking and forward checking which keep assigning values to variables until a solution is found. Finally, we'll look at some heuristics for improving the efficiency of the solver, namely how to order the choosing of the variables, and how to order the assigning of the values to variables.

• The pre-processing routine for binary constraints known as arc-consistency involves calling a pair (x_i, x_j) an arc and noting that this is an ordered pair, i.e., it is not the same as (x_j, x_i). Each arc is associated with a single constraint C_ij, which constrains variables x_i and x_j. We say that the arc (x_i, x_j) is consistent if, for all values a in D_i, there is a value b in D_j such that the assignment x_i = a and x_j = b satisfies constraint C_ij. Note that (x_i, x_j) being consistent doesn't necessarily mean that (x_j, x_i) is also consistent. To use this in a pre-processing way, we take every pair of variables and make it arc-consistent. That is, we take each pair (x_i, x_j) and remove variables from D_i which make it inconsistent, until it becomes consistent. This effectively removes values from the domain of variables, hence prunes the search space and makes it likely that the solver will succeed (or fail to find a solution) more quickly.

• To demonstrate the worth of performing an arc-consistency check before starting asearch for a solution, we'll use an example from Barbara Smith's tutorial. Suppose that we have four tasks to complete, A, B, C and D, and we're trying to schedule them. They are subject to the constraints that:

  • Task A lasts 3 hours and precedes tasks B and C

  • Task B lasts 2 hours and precedes task D

  • Task C lasts 4 hours and precedes task D

  • Task D lasts 2 hours

• We will model this problem with a variable for each of the task start times, namely startA, startB, startC and startD. We'll also have a variable for the overall start time: start, and a variable for the overall finishing time: finish. We will say that the domain for variable start is {0}, but the domains for all the other variables is {0,1,...,11), because the summation of the duration of the tasks is 3 + 2 + 4 + 2 = 11. We can now translate our English specification of the constraints into our formal model. We start with an intermediate translation thus:

  • start ≤ startA

  • startA +3 ≤ startB

  • startA + 3 ≤ startC

  • startB + 2 ≤ startD

  • startC + 2 ≤ startD

  • startD + 2 ≤ finish

• Then, by thinking about the values that each pair of variables can take simultaneously, we can write the constraints as follows:

• C_start,startA= {(0,0), (0,1), (0,2), ..., (0,11)}

• C_startA,start = {(0,0), (1,0), (2,0), ..., (11,0)}

• C_{startA,startB} = {(0,3), (0,4), (0,11), (1,4), (1,5), ..., (8,11)) etc.

• Now, we will check whether each arc is arc-consistent, and if not, we will remove values from the domains of variables until we get consistency. We look first at the arc (start, startA) which is associated with the constraint {(0,0), (0,1), (0,2), ..., (0,11)} above. We need to check whether there is any value, P, in D_start that does not have a corresponding value, Q, such that (P,Q) satisfies the constraint, i.e., appears in the set of assignable pairs. As D_start is just {0}, we are fine. We next look at the arc (startA, start), and check whether there is any value in D_startA, P, which doesn't have a corresponding Q such that (P,Q) is in C_startA, start Again, we are OK, because all the values in D_startA appear in C_startA,_start

• If we now look at the arc (startA, startB), then the constraint in question is: {(0,3), (0,4), (0,11), (1,4), (1,5), ..., (8,11)). We see that their is no pair of the form (9,Q) in the constraint, similarly no pair of the form (10,Q) or (11,Q). Hence, this arc is not arc-consistent, and we have to remove the values 9, 10 and 11 from the domain of startA in order to make the arc consistent. This makes sense, because we know that, if task B is going to start after task A, which has duration 3 hours, and they are all going to have started by the eleventh hour, then task A cannot start after the eighth hour. Hence, we can - and do - remove the values 9, 10 and 11 from the domain of startA.

• This method of removing values from domains is highly effective. As reported in Barbara Smith's tutorial, the domains become quite small, as reflected in the following scheduling network shown in Fig. 6.4.1

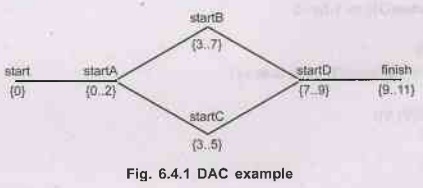
• We see that the largest domain size has only 5 values in it, which means that STOD quite a lot of the search space has been pruned. In practice, to remove as many variables as possible in a CSP which is dependent on precedence constraints, we have to work backwards, i.e., look at the start time of the task, T, which must occur last, then make each arc of the form (startT, Y) consistent for every variable Y. Following this, move on to the task which must occur second to last, etc. In CSPs which only involve precedence constraints, arc-consistency is guaranteed to remove all values which cannot appear in a solution to the CSP. In general, however, we cannot make such a guarantee, but arc-consistency usually has some effect on the initial specification of a problem.

Directional Arc Consistency (DAC)

• The above discussed arc consistency for CSP is not directional at all as each arc is assumed in both directions in the AC-x algorithms. Although, the node and arc consistency algorithms seem easy they are still stronger than necessary for some problems, for example, for enabling backtrack-free search in CSPs which constraints form trees. Therefore yet simpler concept was proposed to achieve some form of consistency, namely, Directional Arc Consistency (DAC) that is defined under total ordering of the variables.

• Definition: A CSP is directional arc consistent under an ordering of variables (0.0) if and only if every arc (V_i, V_j) in its constraint graph such that such that i < j according to the ordering is arc consistent.

• Notice the difference between AC and DAC, in AC we check every arc (V;, V) 92639 while in DAC only the arcs (Vi, Vj) where i < j are considered. Consequently, the arc consistency is stronger than directional arc consistency, i.e., arc consistent CSP Jon is also directional arc consistent but not vice versa (directional arc consistent CSP is not necessarily arc consistent as well).

Algorithm DAC (algorithm for achieving directional arc consistency):

procedure

DAC-1(G)

for

j = nodes (G) | to 1 by -1

do

for each

arc (Vi,Vj) in arcs (G) such that i<j

do

REVISE (Vi,Vj)

end for

end for

end

DAC-1

• In principle, more values can be removed through constraint propagation in more tightly constraint problems. The directional arc-consistency is sufficient for backtrack-free solving of CSPs which constraints form trees. In this case, it is possible to order the nodes (variables) starting from the tree root and concluding at tree leaves. If the graph (tree) is made directional arc-consistent using this order of then it is possible to find the solution by assigning values to variables in the same Jean order. The directional arc-consistency guarantees that for each value of the root (parent) we will find consistent values in daughter. nodes and so on till the values of the leaves. Consequently, no backtracking is necessary to find a complete consistent assignment.