Groups

Groups

Theorem 1. If a and b are any two elements of a group (G, *), then show that G is an abelian group if and only if 

(a * b)² = a² + b²             [A.U A/M 2003, A/M 2011, N/D 2010, M/J 2013]

Proof : If part

Given: G is an abelian group

⇒ Δ a, b Є G, then a*b = b*a ... (1)

To prove: (a * b)² = a² + b²

 (a * b)² = (a*b) * (a*b)

= a* (b*a) *b

= a* (a*b) * b by (1)

= (a * a) * (b * b)

= a² * b²

Only if part

Given : (a*b)² = a² * b² … (2)

To prove : a * b = b * a

(2) ⇒ (a * b)² = a² * b²

⇒ (a * b) * (a * b) = (a * a) * (b * b)

⇒ a* [b * (a * b)] = a * [a * (b * b)]

⇒ b* (a * b) = a * (b * b) [Left cancellation law]

⇒ (b * a) * b = (a * b) * b [Associative law]

⇒ b * a = a * b [Right cancellation law]

⇒ G is an abelian.

Theorem 2. If every element in a group is its own inverse, then the group must be abelian.

(OR)

For any group (G, *) if a² = e with a ≠ e then G is an abelian.

Proof :

Given a = a^-1 for all a Є G.

Let a, b Є G. Then a = a^-1 and b = b^-1

Now (a * b) = (a * b)^-1

i.e., a * b = b^-1 * a^-1

= b * a

⇒ G is abelian.

Theorem 3:

The identity element of a group is unique.         [A.U. M/J 2014]

Proof :

Let (G, *) be a group.

Let e₁ and e₂ be two identity elements in G.

Then

e₁ * e₂ = e₁    [:e₂ is the identity]

e₁* e₂ = e₂      [e₁ is the identity]

Thus e₁ = e₂

Hence the identity is unique.

Theorem 4:

For any element a in a group G, the inverse is unique.

Proof :

Let 'a' be any element of a group G.

If possible let a' and a'' be two inverses of a.

Then

a * a' = a' * a = e ….(i)

a* a'' = a'' *a = e .... (ii)

Now a' = a' * e = a' * (a * a'') = (a' * a) * a'' = e * a" = a"

Hence, the inverse is unique.

(a * b) * (b^-1 * a^-1) = a * (b * b^-1)* a^-1

= a * e * a^-1 = a * a^-1 = e

and (b^-1 * a^-1) * (a * b) = b^-1 * a^-1 * a * b

= b^-1 * e * b

= b^-1 * b = e

(a * b)^-1 = b^-1 * a^-1

Theorem 5.

The identity element is the only idempotent element of a group.

Solution: Given (G, *) is a group.

Since e * e, e is indempotent.

Let a be any idempotent element of G.

Then a * a = a.

e * a = a. [e is the identity element]

It follows that a * a = e * a.

By right cancellation law, we have a = e and so e is the only idempotent element.

Theorem 6.

Thereom: If (G, *) is a finite group of order n, then for any a Є G, we must have aⁿ = e, where e is the identity of the group G.  [M.C.A. M.V. Nov. 96]

Proof : Let 0 (G) = n

Let a Є G

Then order of the sub-group <a> is the order of the element a

If 0 (<a>) = m, then a^m = e and by

Lagrange's theorem, we get

m | n

Let n = mk

Then aⁿ = a^mk = (a^m)^k = e^k = e

Theorem 7:

Every row or column in the composition table of a group (G, *) is a permutation of the elements of G.       [MCA, MU, Dec. 87, Nov. 94, Mar. 96]

Solution: Initially we shall show that no row or column in the composition table can have an element of G more than once.

Let us assume the contrary. Suppose that the row corresponding to an element a Є G has two entries which are both k. That is assume that a * b₁ = a * b₂ = k,  k, b₁, b₂ Є G and b₁ ≠ b₂. Then by cancellation law we have b₁ = b₂ which is a contradiction. A similar result holds for any column. 

Next we will show that every element of G appears in each row and column of the table of compostion. Consider the row corresponding to the element a Є G let b be an arbitrary element of G. Since b = a * (a^{-  1} * b), "b" must appear in the row corresponding to the element a Є G. The same argument applies to every column of the table.

Thus we obtain that no two rows or columns are identical. Hence every row of the composition table is obtained by a permutation of the elements G and that each row is a distinct permutation. The same result applies to the columns of the composition table.

Theorem 8.

Let A = {a₁, a₂, …, a_n} be a finite set with n elements, n ≥ 2.

There are n!/2 even permutations and n!/2 odd permutations.

Proof: Let A_n be the set of all even permutations of A, and let B_n be the set of all odd permutations. We shall define a function f : A_n → B_n, which we show is one to one and onto, and this will show that A_n and B_n have the same number of elements.

Since n ≥2, we can choose a particular transposition q₀ of A. Say that q0 = (a_n-1, a_n). We now define the function f : A_n → B_n by

f (p) = q₀ o p, p Є A_n

Observe that if p Є A_n, then p is an even permutation, so q₀ o p is an odd permutation and thus f(p) Є B_n

Suppose now that P₁ and P₂ are in A_n and ƒ (P₁) = f (P₂). Then

q₀ o p₁ = q₀ o p₂ …. (3)

We now compose each side of equation (3) with q₀:

q₀ o (q₀ o P₁) =  q₀ o (q₀ o P₂);

so by the associative property, (q₀ o q₀) P₁ = (q₀ o q₀) P₂ or, since (q₀ o q₀) = 1_A,

1_A o P₁ = 1_A o P₂

P₁ = P₂

Thus f is one to one.

Now let q Є B_n. Then q₀ o q Є A_n, and

f (q₀ o q) = q₀ o (q₀ o q) = (q₀ o q₀) = 1_A o q = q,

which means that f is an onto function. Since f: A_n → B_n is one to one and onto, we conclude that A_n and B_n, have the same number of elements. Note that A_n ∩ B_n since no permutation can be both even and odd. Also, by Theorem

|A_n U B_n| = n!.

n! = | A_n U B_n| = |A_n| + |B_n| - |A_n ∩ B_n| = 2 |A_n|

We then have

|A_n| = |B_n| = n! / 2

PROBLEMS BASED ON GROUP

Example 1. State any two properties of a group.         [A.U N/D 2010]

Solution: (i) The identity element of a group is unique.

(ii) The inverse of each element is unique.

Example 2. In a group G prove that an element a ЄG such that a² = e, a ≠ e iff a = a^-1

Solution: Let us assume that a = a^-1

Then a² = a * a = a* a⁻¹ = e

Conversely assume that a² = e with a ≠ e.

That is           a * a = e

a^-1 * a * a = a^-1*e

i.e., e * a = a^-1

i.e., a = a^-1

Example 3. Determine whether the set

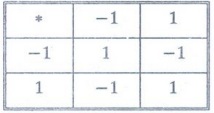
With the binary operation form a group.  [A.U June 2011]

Solution: Yes. '1' is the identity element.

Inverse of each element is the element itself.

Example 4. Define the homomorphism of two groups.  [A.U June 2011]

Solution: Let (G, *) and (H, ∆) be any two groups.

A mapping f: G→H is said to be a homomorphism if f(a*b) = f (a) ∆ f (b), for any a, b Є G

Example 5. If any group (G, *) and a Є G, then (a^-1)^-1 = a

Solution: Given: a^-1 is the inverse of a.

a * a^-1 = a^-1 * a = e

⇒ a is the inverse of a^-1

i.e., (a^-1)^-1 = a

Example 6. If any group (G, *), show that (a * b)^-1 = b^-1 * a^-1

Solution: Given: (G, *) is a group.

∀ a Є G = a^-1 Є G also a * a^-1 = a^-1 * a = e

∀ b Є G = b^-1 Є G also b * b^-1 = b^-1 * b = e

To prove : (a + b)^-1 = b^-1 * a^-1

i.e., To prove : (a * b) * (b^-1 * a^-1) = (b^-1 * a^-1) * (a * b) = e

(a * b) * (b^-1 * a^-1) = a * (b * b^-1) * a^-1

= a * e * a^-1

= a * a^-1               [a * e = a]

= e

(b^-1 * a^-1) * (a * b) = b^-1 * (a^-1 * a) * b

= b^-1 * e * b

= b^-1 * b            [e * b = a]

= e

By (1) and (2), we get

(a * b) * (b^-1 * a^-1) = (b^-1 * a^-1) * (a * b) = e

(a + b)^-1 = b^-1 * a^-1

Example 7. Every group of order 4 is abelian.

Solution: Let (G, *) (be a group of order 4 where G = {e, a, b, c). Since G is of even order, there exists at least one element (say) a such that a^-1 = a

Then two cases arise

(i) b^-1 = b, c^-1 = c, (ii) b^-1 = c, c^-1 = b,

Case (i): e^-1 = e, a^-1 = a, b^-1 = b, c^-1 = c

Every element as its own inverse.

The (G, *) is abelian.

Case (ii):

a^-1 = a, b^-1 = c, c^-1 = b

a² = e, b*c = e, c*b=e

Since (G, *) is a group, its elements will appear in a row (column) only once.

Since, a, e appears in the second row and b appears in the third column, c will appear as (2, 3)th element.

 (2, 4)th element is b

(3, 3)th element is a

(3, 2)th element is c

(4, 2)th element is b

(4, 4)th element is a

Example 9. Show that the set S = {1, 5, 7, 11} is a group w.r.t. multiplication modulo 12.

Solution: The composition tables of S w.r.t O₁₂ of as follows :

Here 5 O₁₂ 7 = 35, which on division by 12 gives the remainder 11, 11 O₁₂ 7 = 77, which on division by 12 gives the remainder 5 etc.

Hence S is a group, in which 1 is the identity and each element of S is its own inverse.

Example 10. Show that the set of matrices

Example 11. Find the left cosets of {[0], [3]} in the addition modular group (Z₆, +₆).    [MCA, N/D. 2002][A.U N/D 2010]

Solution: Let Z₆ = {[0], [1], [2], [3], [4], [5], [6]} be a group and H = {[0], [3]} be a sub-group of Z₆ under +₆ (addition mod 6)

The left cosets of H are

 [0] + H = {[0], [3]}

[1] + H = {[1], [4]}

[2] + H = {[2], [5]}

[3] + H = {[3], [6]} = {[3], [0]} = {[0], [3]} = H

[4] + H = {[4], [7]} = {[4], [1]} = [1] + H

[5] + H = {[5], [8]} = {[5], [2]} = [2] + H

[0] + H = [3] + H = H

and  [1] + H = [4] + H, [2] + H = [5] + H

are the distinct left cosets of H in Z₆

Example 12. If f: G→G' is a group homomorphism from {G, *} to {G', ∆) then prove that for any a Є G, f(a^-1) = [f (a)]^-1     [A.U N/D 2012]

Solution: ∀ a Є G and ∀ a^-1 Є G

f(a * a^-1) = f (a) ∆ f (a^-1)

i.e., f(e) = f (a) ∆ f (a^-1).

i.e., e' = f (a) ∆ f (a^-1) .... (1)

|||^1y, ƒ (a^-1 * a) = ƒ (a^-1) ∆ ƒ (a)

i.e., f(e) = f(a^-1) ∆ f(a)

e' = ƒ (a^-1) ∆ ƒ (a) .... (2)

From (1) & (2), we get

f (a) ∆ ƒ (a^-1) = f (a^-1) ∆ ƒ(a)

⇒ f(a^-1) is the inverse of ƒ(a)

i.e., ƒ (a^-1) = [ƒ(a)]^-1

Example 13. Let G be a group and a Є G. Let f : G→G be given by f(x) = a x a^-1 G for all x Є G. Prove that f is an isomorphism of G on to G.    [A.U. A/M. 2005, N/D 2010]

Solution: The map ƒ is a homomorphism if x, y Є G, then

ƒ (x) ƒ (y) = (axa^-1) (aya^-1)

= ax (a^-1a) ya^-1  

= axya^-1

= a (xy) a^-1 = f (xy).

So f is a homomorphism.

f is one-to-one: If f(x) = f(y), then axa^-1 = aya^-1, so by left cancellation, we have xa^-1 = ya^-1, again by right cancellation, we get x = y.

f is onto : Let y Є G, then a^-1 y a Є G and f(a^-1ya)

= a (a^-1 ya) a^-1

= (aa^-1) y (aa^-1)

= y.   So f (x) = y for some x Є G.

Thus f is an isomorphism.

PERMUTATION FUNCTIONS 

Definition :

A bijection from a set A to itself is called a permutation of A.

Example 14: Let A=R and let f: A → A be defined by f(a) = 2a+1. Since ƒ is one to one and onto, it follows that ƒ is a permutation of A.

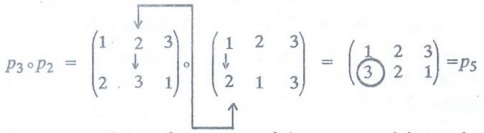
Example 15: Let A = {1, 2, 3}. Then all the permutations of A are

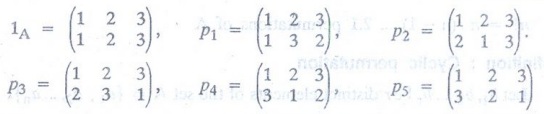
Using the permutations of compute

(a) p₄^-1; (b) P₃ o P₂

Solution: (a) Viewing p₄ as a function, we have

P4 = {(1, 3), (2, 1), (3, 2)}

Then P₄^-1 = {(3, 1), (1, 2), (2, 3)}

or, when written in increasing order of the first component of each ordered pair, we have

p₄^-1 = {(1, 2), (2, 3), (3, 1)}

Theorem : If A = (a₁, a₂, ... a_n} is a set containing n elements, then there are n! = n. (n - 1) … 2.1 permutations of A

Definition: Cyclic permutation

Let b₁, b₂, ... b_r be r distinct elements of the set A = {a₁, a₂, ... a_n}. 

The permutation p: A→ A defined by

p (b₁) = b₂

p (b₂) = b₃

.

.

.

p (b_r-1) = b_r

p (b_r) = b₁

p(x) = x, if x Є A, x €{b1, b2, … b_r) is called a cyclic permutation of length r, or simply a cycle of length r, and will be denoted by (b₁, b₂, … b_r).

Example 16: Let A = {1, 2, 3, 4, 5}. The cycle (1, 3, 5) denotes the permutation

Example 17: Let A = {1, 2, 3, 4, 5, 6}, Compute (4, 1, 3, 5) o (5, 6, 3) and (5, 6, 3) o (4, 1, 3, 5).

Solution: We have

Observe that

(4, 1, 3, 5) o (5, 6, 3) ≠ (5, 6, 3) o (4, 1, 3, 5)

and that neither product is a cycle.

Definition :

Two cycles of a set A are said to be disjoint if no element of A appears in both cycles.

Example 18: Let A = {1, 2, 3, 4, 5, 6}. Then the cycles (1, 2, 5) and (3, 4, 6) are disjoint, whereas the cycles (1, 2, 5) and (2, 4, 6) are not.

Theorem: A permutation of a finite set that is not the identity or a cycle can be written as a product of disjoint cycles of length >2.

Example 19: Write the permutation  of the set A = {1, 2, 3, 4, 5, 6, 7, 8} as a product of disjoint cycles.

Solution: We start with 1 and find that p (1) = 3, p (3) = 6, and p (6) = 1, so we have the cycle (1, 3, 6). Next we choose the first element of A that has not appeared in a previous cycle. We choose 2, and we have p (2) = 4, p (4) = 5 and p (5) = 2, so we obtain the cycle (2, 4, 5). We now choose 7, the first element of A that has not appeared in a previous cycle. Since p (7) = 8 and p (8) = 7, we obtain the cycle (7, 8). We can then write p as product of disjoint cycles as

p. = (7, 8) o (2, 4, 5) o (1, 3, 6).

Definition: Even and Odd Permutations

A cycle of length 2 is called a transposition. That is, a transposition is a cycle p = (a_i, a_j), where p (a_i) = a_j and p (a_j) = a_i.

Observe that if p = (a_i, a_j) is a transposition of A, then p o p = 1A, the identity permutation of A.

Every cycle can be written as a product of transpositions. In fact,

(b₁, b₂, ... b_r) = (b₁, b_r) o (b₁, b_r-1) o...o (b₁, b₃) o (b₁, b₂)

This case can be verified by induction on r, as follows:

Basis Step

If r = 2, then the cycle is just (b₁, b₂), which already has the proper form.

Induction Step

We use P (k) to show P (k + 1). Let (b₁, b₂ ... b_k, b_{k + 1}) be a cycle of length k+1. Then (b₁, b₂, ... b_k, b_{k + 1}) = (b₁, b_k+1) o (b₁, b₂, ... b_k) as may be verified by computing the composition. Using P(k), (b₁, b₂, ... b_k) = (b₁, b_k) o (b₁, b_k-1) o ... o (b₁, b₂). Thus, by substitution,

(b₁, b₂, ... b_{k + 1}) = (b₁, b_{k + 1}) o (b₁, b_k)o ... o(b₁, bз) (b₁, b₂).

This completes the induction step. Thus, by the principle of mathematical induction, the result holds for every cycle. For example,

(1, 2, 3, 4, 5) = (1, 5) o (1, 4) o (1, 3) o (1, 2)

Corollary 1: Every permutation of a finite set with atleast two elements can be written as a product of transpositions.

Theorem: If a permutation of a finite set can be written as a product of an even number of transpositions, then it can never be written as a product of an odd number of transpositions, and conversely.

A permutation of a finite set is called even if it can be written as a product of an even number of transpositions, and it is called odd if it can be written as a product of an odd number of transpositions.

Example 20: Is the permutation  even or odd ?

Solution: We first write p as a product of disjoint cycles, obtaining

P = (3, 5, 6) o (1, 2, +, 7).

Next we write each of the cycles as a product of transpositions :

(1, 2, 4, 7) = (1, 7) o (1, 4) o (1, 2)

(3, 5, 6) = (3, 6) о (3, 5)

Then p = (3, 6) o (3, 5) o (1, 7).o (1, 4) o (1, 2). Since p is a product of an odd number of transpositions, it is an odd permutation.

Note: From the definition of even and odd permutations, it follows.

(a) The product of two even permutation is even.

(b) The product of two odd permutations is even.

(c) The product of an even and an odd permutation is odd.

Example 21: Show that the permutation

EXERCISE

1. Which of the following functions f: Z →Z permutations of Z ?

(a) f is defined by f (a) = a + 1

(b) f is defined by f (a) = (a - 1)².

2. Which of the following functions f: R→ R are permutations of R?

(a) f is defined by f (a) = a³

(b) f is defined by f (a) = e^a

3. Which of the following functions f: R→R are permutations of R?

(a) f is defined by f (a) = a -1.

(b) f is defined by f (a) = a².

4. Which of the following functions f: Z→Z are permutations of Z?

(a) f is defined by f (a) = a² + 1.

(b) f is defined by f (a) = a³ - 3

5. Let A = {a, b, c, d, e, f, g}. Write each permutation as the product of disjoint cycles.

6. Let A = {1, 2, 3, 4, 5, 6, 7, 8}. Write each permutation as a

product of transpositions.

(a) (2, 1, 4, 5, 8, 6)

(b) (3, 1, 6) o (4, 8, 2, 5)

7. Code the message WHERE ARE YOU by applying the permutation (1, 7, 3, 5, 11) o (2, 6, 9) o (4, 8, 10).

8. Decode the message ATEHAOMOMNTI, which was encoded using the permutation ?

(3, 7, 1, 12) o (2, 5, 8) o (4, 10, 6, 11, 9)

9. Let A = {1, 2, 3, 4, 5, 6, 7, 8}. Determine whether the permutation is even or odd ?

(c) (6, 4, 2, 1, 5)

(d) (4, 8) о (3, 5, 2, 1) o (2, 4, 7, 1)

10. Prove that the product of two even permutation is even.

11. Prove that the product of two odd permutation is even.

12. Prove that the product of an even and odd permutation is odd.

13. Let A = {1, 2, 3, 4, 5}. Let f (5, 2, 3) and g = {3,4,1) be permutations of A. Compute each of the following and write the result as the product of disjoint cycles.

(a) f o g,

(b) f^-1 o g^-1