Graphs for Quantitative Data

Graphs for Quantitative Data

1. Histogram

• A histogram is a special kind of bar graph that applies to quantitative data (discrete or continuous). The horizontal axis represents the range of data values. The bar height represents the frequency of data values falling within the interval formed by the width of the bar. The bars are also pushed together with no spaces between them.

• A diagram consisting of rectangles whose area is proportional to the frequency of a variable and whose width is equal to the class interval.

• Here the data values only take on integer values, but we still split the range of values into intervals. In this case, the intervals are [1,2), [2,3), [3,4), etc. Notice that this graph is also close to being bell-shaped. A symmetric, bell-shaped distribution is called a normal distribution.

• Fig. 2.4.1 shows histogram.

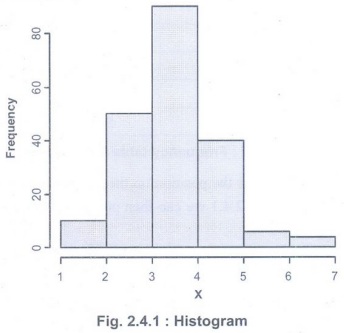
• Notice that all the rectangles are adjacent and they have no gaps between them unlike a bar graph.

• This histogram above is called a frequency histogram. If we had used the relative frequency to make the histogram, we would call the graph a relative frequency histogram.

• If we had used the percentage to make the histogram, we would call the graph a percentage histogram.

• A relative frequency histogram is the same as a regular histogram, except instead of the bar height representing frequency, it now represents the relative frequency (so the y-axis runs from 0 to 1, which is 0% to 100%).

2. Frequency polygon

• Frequency polygons are a graphical device for understanding the shapes of distributions. They serve the same purpose as histograms, but are especially helpful for comparing sets of data. Frequency polygons are also a good choice for displaying cumulative frequency distributions.

• We can say that frequency polygon depicts the shapes and trends of data. It can be drawn with or without a histogram.

• Suppose we are given frequency and bins of the ages from another survey as shown in Table 2.4.1.

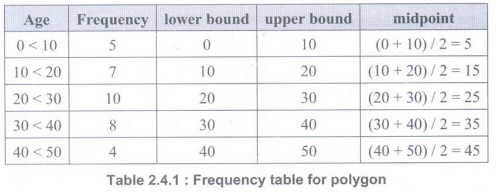
• The midpoints will be used for the position on the horizontal axis and the frequency for the vertical axis. From Table 2.4.1 we can then create the frequency polygon as shown in Fig. 2.4.2.

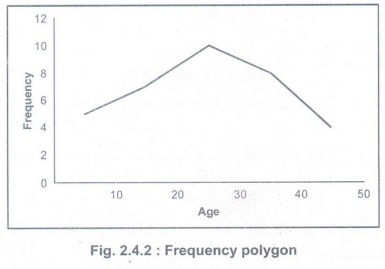
• A line indicates that there is a continuous movement. A frequency polygon should therefore be used for scale variables that are binned, but sometimes a frequency polygon is also used for ordinal variables.

• Frequency polygons are useful for comparing distributions. This is achieved by overlaying the frequency polygons drawn for different data sets.

Example 2.4.1: The frequency polygon of a frequency distribution is shown below.

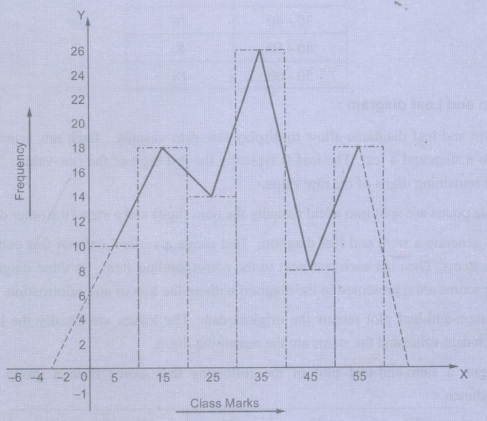
Answer the following about the distribution from the histogram.

(i) What is the frequency of the class interval whose class mark is 15?

(ii) What is the class interval whose class mark is 45?

(iii) Construct a frequency table for the distribution.

• Solution:

(i) Frequency of the class interval whose class mark is 15 → 8

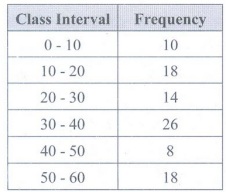
(ii) Class interval whose class mark is 45→40-50

 (iii) As the class marks of consecutive overlapping class intervals are 5, 15, 25, 35, 45, 55 we find the class intervals are 0 - 10, 10-20, 20 - 30, 30 - 40, 40 - 50, 50 - 60. Therefore, the frequency table is constructed as below.

3. Steam and Leaf diagram:

• Stem and leaf diagrams allow to display raw data visually. Each raw score is divided into a stem and a leaf. The leaf is typically the last digit of the raw value. The stem is the remaining digits of the raw value.

• Data points are split into a leaf (usually the ones digit) and a stem (the other digits)

• To generate a stem and leaf diagram, first create a vertical column that contains all of the stems. Then list each leaf next to the corresponding stem. In these diagrams, all of the scores are represented in the diagram without the loss of any information.

• A stem-and-leaf plot retains the original data. The leaves are usually the last digit in each data value and the stems are the remaining digits.

• Create a stem-and-leaf plot of the following test scores from a group of college freshmen.

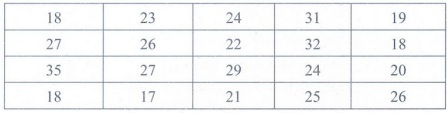
• Stem and Leaf Diagram :