Graphs and Graph Models

UNIT III: GRAPHS

SYLLABUS

Graphs and graph models - Graph terminology and special types of graphs -  Representing graphs and graph isomorphism - connectivity - Euler and Hamilton paths.

Graphs and Graph Models

Definition: Graph

A graph G = (V(G), E (G)) concists of V, a non empty set of vertices (nodes or points) and E, a set of edges (also called lines).

i.e., A graph G is an ordered triple (V (G), E (G), ϕ) consists of a non-empty set V called the set of vertices (nodes or points) of the graph G, E is said to be the set of edges of the graph G, and is a mapping from the set of edges E to a set of order or un ordered pairs of elements of V.

Example :

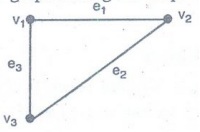
Let G = (V (G), E (G), ϕ) where V (G)= {v₁, v₂, v₃, v₄} E (G)=(e₁, e₂, e₃, e₄, e₅) and ϕ is defined by ϕ (e₁) = {v₁, v₂}, ϕ (e₂) = {v₂, v₃}, ϕ (e₃) = {v₃, v₄}, ϕ (e₄) = {v₄, v₁}, ϕ (e₅) = {v₁, v₃}

Now the diagramatic form of G is as follows.

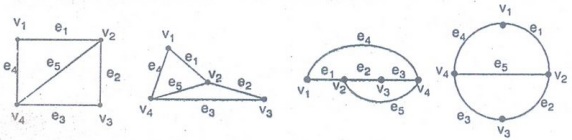
It should be noted that, in drawing a graph, it is immaterial whether the edges are drawn straight or curved, long or short, the important point is how the vertices are joined up.

The above graphs are same.

Note: 1. We denote the graph G as G (V, E) or simply as G.

2. If e ϵ E is an edge and ϕ (e) = {v₁, v₂}, then we say that e is an edge joining v₁ and v₂, and the vertices v₁ and v₂ are called the ends (end vertices) of e.

3. If graphs, an edge should not pass through any points (vertices) other than the two end vertices of the edge.

Definition: Adjacent vertices

Any pair of vertices which are connected by an edge in a graph is called adjacent vertices.

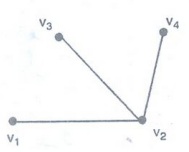
Here v₁, v₂ ; v₂, v₄ ; v₂, v₃ are adjacent vertices

v₁, v₃ ; v₃, v₄ ; v₁ v₄ are not adjacent.

Definition: Adjacent edges:

If two distinct edges are incident with a common vertex then they are called adjacent edges.

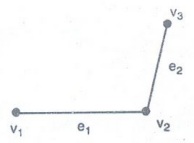
Here e₁ and e₂ are incident with a common vertex v₂.

Definition: Isolated vertex

In any graph, a vertex which is not adjacent to any other vertex is called an isolated vertex. Otherwise the vertex has no incident edge.

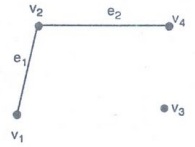
Here v₃ has no incident edge. Therefore the vertex v₃ is called isolated vertex.

Note :

1. A graph with p vertices and q edges is called a (p, q) graph.

2. The graph (p, 0) is trivial or null graph.

3. If any two edges are intersected then their intersection is not considered as a vertex.

4. The set of edges in a null graph is empty.

Definition: Label graph

A graph in which each vertex is assigned a unique name or label is called a label graph.

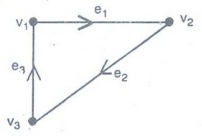
Definition: Directed graph and undirected graph

In a graph G (V, E), an edge which is associated with an ordered pair of vertices is called a directed edge of graph G, while an edge which is associated with an unordered pair of vertices is called an undirected edge.

A graph in which every edge is directed is called a directed graph simply a digraph.

A graph in which every edge is undirected is called an undirected graph.

The end vertices of an edge are said to be incident with the edge and vice versa.

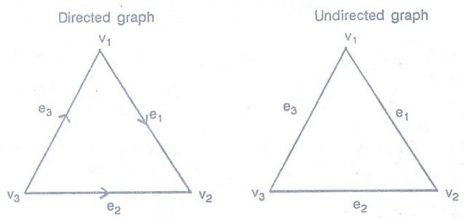
The edge e₁ is incident with the vertices v₁ and v₂ also the vertex v₁ is incident with  e₁ and e₃.

The vertices v₁ and v₂ are also called the initial and terminal vertices of the edge e₁.

Definition: Mixed graph

If some edges are directed and some are undirected in a graph, then the graph is a mixed graph.

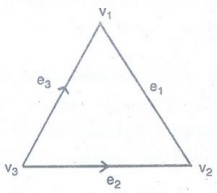
Definition: Loop

A loop is an edge whose vertices are equal.

i.e., An edge of a graph which joins a vertex to itself is called a loop.

Definition: Parallel edges (Multiple edges)

Multiple edges are edges having the same pair of vertices.

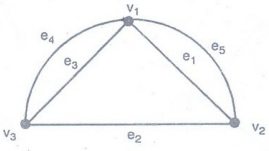
Definition: Multi graph

Any graph which contains some parallel edges and loops is called as multi graph.

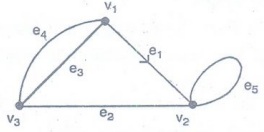
Definition: Simple graph

A simple graph is a graph having no loops or multiple edges.

Definition: Simple directed graph

When a directed graph has no loops and has no multiple directed edges, it is called a simple directed graph.

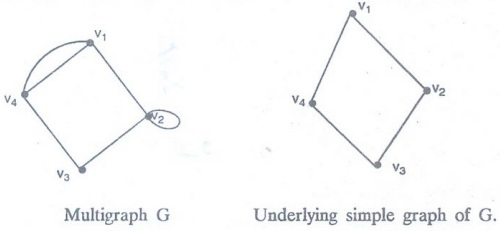
Definition: Underlying simple graph

A graph obtained by deleting all loops and parallel edges from a graph is called underlying simple graph.

Definition : Finite graph

A graph G is finite if and only if both the vertex set V(G) and the edge set E (G) are finite, otherwise the graph is infinite.

Example : Let V(G) = Z and E (G) = {eij / |i-j| = 1} clearly, the graph G is infinite.

Note: Hereafter, a graph means that is a finite graph unless otherwise stated.

Definition: Multiplicity m.

When there are m directed edges, each associated to an ordered pair of vertices (u, v), we say that (u, v) is an edge of multiplicity m.

Definition: Weighted graph

A graph in which weights are assigned to every edge is called a weighted graph.

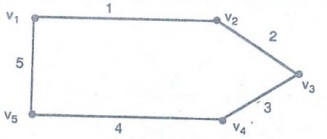
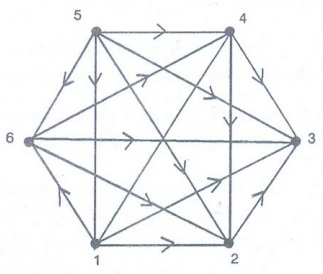
here 1, 2, 3, 4, 5 are weights assigned to each edge respectively.

Note :

If the graph G is finite, |V| denotes the number of vertices of G known as order of G and |E| denotes the number of edges of G, known as size of G,

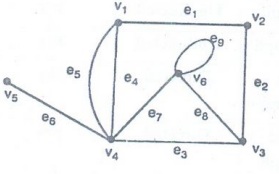
For this graph |V| = 6; |E| = 9

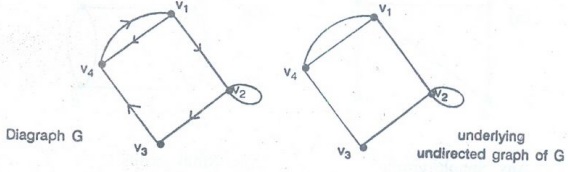
Definition: Underlying undirected graph

A graph obtained by ignoring the direction of edges in a directed graph is called underlying undirected graph.

Definition Pseudographs :

Graphs that may include loops, and possibly multiple edges connecting the same pair of vertices, are sometimes called Pseudographs.

Example 1. What type of graph the following are

Example 2. The diagram shows a multigraph G, Why G is not a simple graph ?

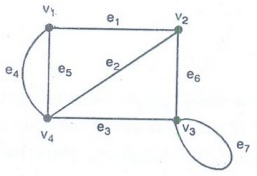
Solution: G is not a simple graph since it contains multiple edges e₄, e₅ also a loop e₇.

Example 3. Describe formally the graph given below :

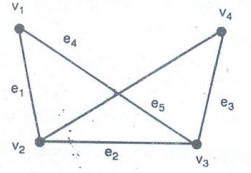
Solution : G = (V,E)

V = {v₁, v₂, v₃, v₄}

E = {e₁, e₂, e₃, e₄, e₅}

E (a) = {(v₁, v₂), (v₂, v₃), (v₃, v₄), (v₁, v₃), (v₂, v₄)}

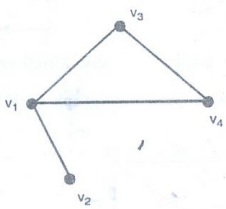
Example 4. Draw a diagram for the following graph

G = G(V,E)

V = {v₁, v₂, v₃, v₄}

E = {(v₁, v₂), (v₄, v₁), (v₃, v₁), (v₃, v₄)}

Solution :

Example 5. Let G be a simple graph. Show that the relation R on the set of vertices of G such that uRv if and only if there is an edge associated to {u, v} is a symmetric, irreflexive relation on G.

Solution :

Given: "G is a simple graph, R is a relation to (u, v)

(i) To prove symmetric

i.e., to prove uRv ⇒ vRu                                                           

If u R v, then there is an edge associated with {u, v}

But {u,v} = {v, u} so this edge is associated with {v, u}

⇒ v R u

(ii) To prove irreflexive :

A simple graph doesnot allow loops,

u R u never holds.

irreflexive.

Graph Models

1. Niche overlap, Graphs in Ecology.

A niche overlap graph is a simple graph because no loops or multiple edges are needed in this model.

For example, the competition between species by a vertex. An undirected edge connects two vertices if the two species represented by these vertices compete (i.e., some of the food resources they use are the same)

Example : Construct a niche overlap graph for six species of birds, where the hermit thrush competes with the robin and with the blue jay, the robin also competes with the mocking-bird, the mockingbird also competes with the blue jay, and the nuthatch competes with the hairy woodpecker.

Solution:

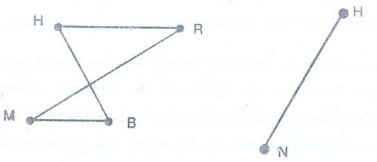
2. Acquaintanceship graphs.

In this graph no multiple edges and no loops are used. The acquaintanceship graph of all people in the world has more than six billion vertices and probably more than one trillion edges!

Example: Draw a graph to represent whether each pair of the computer scientists with biographies who died before 1900 were contemporaneous. (Assume two people lived at the same time if they were alive during the same year).

Solution :

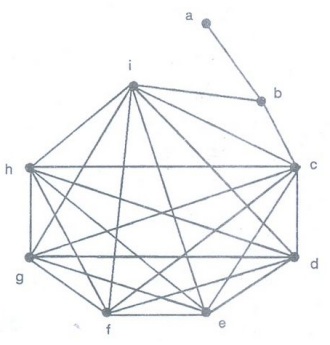
Let a → Goldback

b → Vandermonde

c → Gauss

d → Dodgson

e → Boole

f → Lovelace

g → Demorgan

h → Dirichlet

i → Lam

3. Influence Graphs.

A directed graph called an influence graph can be used to study group behaviour. Each person of the group is represented by a vertex. There is a directed edge from vertex a to vertex b when the person represented by vertex a influences the person represented by vertex b. This graph does not contain loops and it does not contain multiple directed edges.

Example: Construct an influence graph for the board members of a company if the President can influence the Director of Research and Development, the Director of Marketing, and the Director of Operations ; the Director of Research and Development can influence the Director of Operations; the Director of Marketing can influence the Director of Operations; and no one can influence, or be influenced by, the Chief Financial Officer.

Solution :

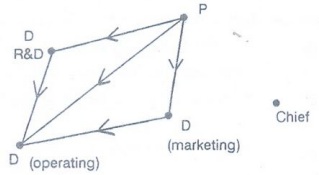
4. The Hollywood Graph:

The Hollywood graph represents actors by vertices and connects two vertices when the actors represented by these vertices have acted together one a movie. This graph is a simple graph since its edges are undirected, it contains no multiple edges, and it contains no loops.

5. Round-Robin Tournaments:

In a tournament where each team plays each other team exactly once is called a round-robin tournament. It can be modeled using directed graphs where each team is represented by a vertex. Note that (a, b) is an edge if team a beats team b. This graph is a simple directed graph, containing no loops or multiple directed edges (because no two teams play each other more than once). Such a directed graph model is presented in figure. We see that Team 5 is undefeated in this tournament, and Team 3 is winless.

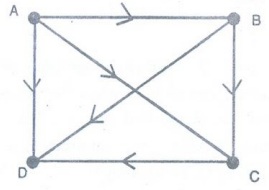
Example: In a round-robin tournament the A team beat the B team, the A team beat the C team, the A team beat the D team, the B team beat the C team, the B team beat the D team, and the C team beat the D team. Model this outcome with a directed graph?

Solution :

6. Call Graphs:

A directed multigraph can be used to model calls where each telephone number is represented by a vertex and each telephone call is represented by a directed edge. The edge representing a call starts at the telephone number from which the call was made and ends at the telephone number to which the call was made. We need directed edges since the direction in which the call is made matters. We need multiple directed edges since we want to represent each call made from a particular telephone number to a second number.

7. Collaboration Graphs:

This graph is a simple graph because it contain undirected edges and has no loops or multiple edges.

In Colloaboration graph, vertices represent people and edges link two people if they have jointly written a paper.

8. Precedence Graphs and Concurrent Processing:

The dependence of statements on previous statements can be represented by a directed graph. Each statement is represented by a vertex, and there is an edge from one vertex to a second vertex if the statement represented by the second vertex cannot be executed before the statement represented by the first vertex has been executed. This graph is called a precedence graph.

S₁ a:= 0

S₂ b:= 1

S₃ C:= a + 1

S₄ d:= b + a

S₅ e:= d + 1

S₆ e:= c + d

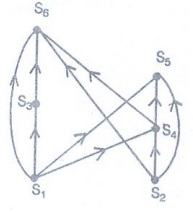
9. Roadmaps:

Roadmaps depicting only one-way roads and no loop roads, and where no two roads start at the same intersection and end at the same intersection, can be modeled using simple directed graphs. Mixed graphs are needed to depict roadmaps that include both one-way and two-way roads.

10. The Web Graph:

The World Wide Web can be modeled as a directed graph where each Web page is represented by a vertex and whre an edge starts at the Web page a and ends at the Web page b if there is a link on a pointing to b. Since new Web pages are created and others removed somewhere on the Web almost every second, the Web graph changes on an almost.

EXERCISE 3.1

1. The intersection graph of a collection of sets B₁, B₂, ..., B_n is the graph that has a vertex for each of these sets and has an edge connecting the vertices representing two sets if these sets have a nonempty intersection. Construct the intersection graph of these collections of sets.

(a) B₁ = {..., -4, -3, -2, -1, 0}

B₂ = {..., -2, -1, 0, 1, 2, ...}

B₃ = {..., -6, -4, -2, 0, 2, 4, 6, ...}

B₄ = {..., -5, -3, -1, 1, 3, 5, ...}

B₅ = {..., -6, -3, 0, 3, 6, ...}

(b) B₁ = {x | x < 0}

B₂ =   {x | -1<x<0}

B₃ = {x | 0 < x < 1}

B₄ = {x | -1 < x < 1}

B₅ = {x | x > -1}

B₆ = R

(c) B₁ = {0, 2, 4, 6, 8}, B₂ = {0, 1, 2, 3, 4}

B₃ = {1, 3, 5, 7, 9}, B₄ = {5, 6, 7, 8, 9}

B₅ = {0, 1, 8, 9}

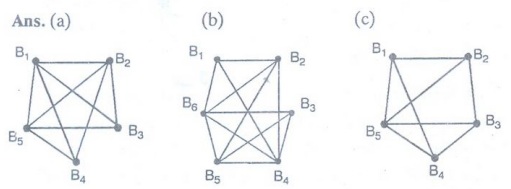
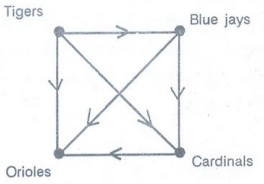
2. In a round-robin tournament the Tigers beat the Blue Jays, the Tigers beat the Cardinals, the Tigers beat the Orioles, the Blue Jays beat the Cardinals, the Blue Jays beat the Orioles, and the Cardinals beat the Orioles. Model this outcome with a directed graph.

[Ans.

3. (a) Explain how graphs can be used to model electronic mail messages in a network. Should the edges be directed or undirected? Should multiple edges be allowed? Should loops be allowed?

(b) Describe a graph that models the electronic mail sent in a network in a particular week.

4. How can a graph that models e-mail messages sent in a network be used to find people who have recently changed their primary e-mail address?

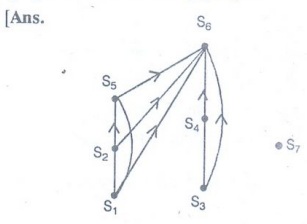
5. Construct a precedence graph for the following program :

S₁: x : = 0

S₂: x: = x+2

S₃: y: = 3

S₄: z: = y

S₅: x: = x + 3

S₆: y: = x + z

S₇: z: = 4

[Ans.

6. Describe a graph model that represents whether each person at a party knows the name of each other person at the party. Should the edges be directed or undirected? Should multiple edges be allowed? Should loops be allowed?

[Ans. Let A be the set of people at the party. Let B be the set of ordered pairs (u, v) in V ˟ V such that u knows v's name. The edges are directed, but multiple edges are not allowed. Lierally, there is a loop at each vertex, but for simplicity, the model could omit the loops.