Graph Terminology and Special Types of Graphs

Graph Terminology and Special Types of Graphs

Definition: Two vertices u and v in an undirected graph G are called adjacent (or neighbors) in G if u, v are endpoints of an edge of G.

If e is associated with (u, v), the edge e is called incident with the vertices u and v. The edge e is also said to connect u and v.

The vertices u and v are called endpoints of an edge associated with (u, v).

Definition: The degree of a vertex :

The degree of a vertex in an undirected graph is the number of edges incident with it, except that a loop at a vertex contributes twice to the degree of that vertex.

The degree of the vertex is denoted by deg( ).

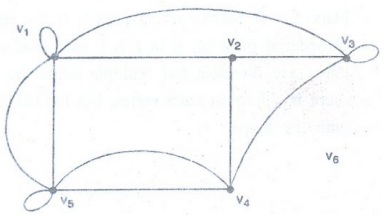
Example :

Let v be a vertex in a graph G. Then the degree d_G(V) of the incident with v (each loop is counted twice). The d_G(V) can also be denoted by deg G(V) (or explicity, we use d (V) or deg (V) to denote the degree of V).

deg (V₁) = 6

deg (V₂) = 3

deg (V₃) = 5

deg (V₄) = 4

deg (V₅) = 6

deg (V₆) = 0

Note :

1. Let G be an undirected graph with |E| edges and |V| = n vertices, then Σⁿ_i=1 deg (v_i) = 2 |E|.

2. In any graph, the number of vertices of odd degree is even.

3. A vertex of degree one is called a pendant or end vertex in G.

4. A vertex of degree zero is called an isolated vertex in G.

5. Two adjacent edges are said to be in series if their common vertex is of degree two.

The vertices V₄, V₆ are pendant vertices.

The vertices V₅, V₇ are isolated vertices.

Example 1. What are the degrees of the vertices in the graph G.

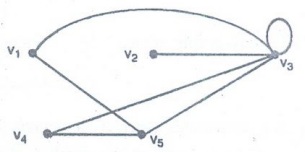
Solution :

deg (v₁) = 2, deg (v₂) = 1, deg (v₃) = 6

deg (v₄) = 2, deg (v₅) = 3.

Example 2. How many edges are there in a graph with 10 vertices each of degree six ?

Solution: Sum of the degrees of the 10 vertices

is (6) (10) = 60

i.e., 2e = 60

e = 30

Example 3. Show that the sum of degree of all the vertices in a graph G, is even.

Proof : Each edge contribute two degrees in a graph.

Also, each edge contributes one degree to each of the vertices on which it is incident.

Hence, if there are N edges in G, then

2N = d (v₁) + d (v₂) + …. + d (v_N)

Thus, 2 N is always even.

[The Handshaking Theorem]                  [A.U N/D 2012]

Theorem: For any graph G with E edges and V vertices

v₁, v₂, …., v_n,  Σⁿ_i=1 d (v_i) = 2 E

Proof :

Let G = G (V,E) be any graph, where V = {v₁, v₂, …, v_n} and E = (e₁, e₂,..., e_n}

Since, each edges contributes twice as a degree, the sum of the degree of all vertices in G is twice as the number of edges in G.

i.c., Σⁿ_i=1 d (v_i) = 2 |E| = 2e

Note: This theorem applies even if multiple edges and loops are present.

Theorem: The number of odd degree vertices is always even.

Let G = {V, E} be any graph with 'n' number of vertices and 'e' number of edges.

Let V₁, 2, …,V_k be the vertices of odd degree and V₁', V₂', ..., V_m' be the vertices of even degree.

To prove, k is even

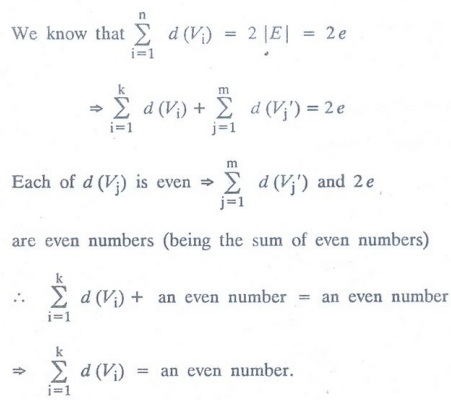
Since, each term d (V_i) is odd.

Therefore, the number of teams in the LHS sum must be even.

⇒ K is even.

Hence, the theorem.

Example 4. Verify that the sum of the degree of all the vertices is even for the graph.

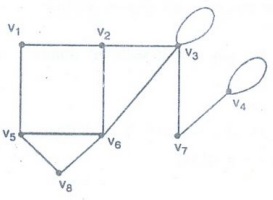
Solution: The sum of degree of all the vertices is

= d (v₁) + d (v₂) + d (v₃) + d (v₄) + d (v₅) + d (v₆) + d (v₇) + d (v₈)

= 2 + 3 + 5 + 3 + 3 + 4 + 2 + 2

= 24 which is even.

Note: Odd vertices means vertices of odd degree.

Example 5. Verify the handshaking theorem for the graph.

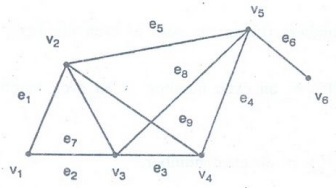
Solution: To prove Σ deg (v_i) = (2) (no. of edges)

i.e., Σ deg (v_i) = (2) (9) = 18

Σ deg (v_i) = deg (v₁) + deg (v₂) + deg (v₃) + deg (v₄) + deg (v₅) + deg (v₆)

= 2 + 4 + 4 + 3 + 4 + 1

= 18

Hence the theorem is true.

Theorem: A simple graph with at least two vertices has at least two vertices of same degree.

Proof: Let G be a simple graph with n ≥ 2 vertices.

The graph G has no loop and parallel edges.

Hence the degree of each vertices is ≤ n - 1.

Suppose that all the vertices of G are of different degrees.

Following degrees 0, 1, 2, 3, …, n - 1 are possible for n vertices of G.

Let u be the vertex with degree 0. Then u is an isolated vertex.

Let v be the vertex with degree n - 1 then v has n - 1 adjacent vertices.

Because v is not an adjacent vertex of itself, therefore every vertex of G other than u is an adjacent vertex of G other than u is an adjacent vertex u.

Hence u cannot be an isolated vertex, this contradiction proves that a simple graph contains two vertices of same degree.

Note: The converse of the above theorem is not true.

Example 6. Show that the degree of a vertex of a simple graph G on n vertices cannot exceed n-1.

Solution: Let v be a vertex of G because G is simple, no multiple edges or loops are allowed in G. Thus v can be adjacent to at most all the remaining n - 1 vertices of G.

Hence v may have maximum degree n - 1 in G.

Then 0 ≤ deg G(v) ≤ n − 1 ∀ v ϵ V(G)

Example 7. Show that in a group, there must be two people who know the same number of other people in the group.

Solution: Construct the simple graph model in which V is the set of people in the group and there is an edge associated with (u, v) if u and v know each other. Then the degree of vertex v is the number of people v knows.

We know that there are two vertices with the same degree. Therefore there are two people who know the same number of other people in the group.

Example 8. Is there a simple graph corresponding to the following degree sequences?  (i) (1, 1, 2, 3) (ii) (2, 2, 4, 6)

Solution :

(i) There are odd number (3) of odd degree vertices, 1, 1 and 3. Hence there exist no graph corresponding to this degree sequence.

(ii) Number of vertices in the graph sequence is four and the maximum degree of a vertex is 6 which is not possible as the maximum degree cannot exist one less than the number of vertices.

Example 9. Show that the maximum number of edges in a simple graph with n vertices is n (n - 1) / 2

Solution: Use handshaking theorem.

i.e,. Σ_i=1 d (v_i) 2 e,

where e is the number of edges with n vertices in the graph G.

i.e., d (v₁) + d (v₂) + ... d (v_n) = 2e  ….. (1)

Since we know that the maximum degree of each vertex in the graph G can be (n - 1)

(1) ⇒ (n − 1) + (n − 1) + ... to n terms = 2e

⇒ n (n − 1) = 2e

e = n (n - 1) / 2

Hence the maximum number of edges in any simple graph with n vertices is n (n - 1) / 2

Definition: When (u, v) is an edge of the graph G with directed edges, u is said to be adjacent to v and v is said to be adjacent from u.

The vertex u is called the initial vertex of (u, v), and v is called the terminal or end vertex of (u, v).

The initial vertex and terminal vertex of a loop are the same.

Definition: In a graph with directed edges the in-degree of a vertex v, denoted by deg ^-  (v), is the number of edges with v as their terminal vertex.

The out-degree of with v, denoted by deg ⁺ (v), is the number of edges with v as their initial vertex.

Note: A loop at a vertex contributes 1 to both the in-degree and the out-degree of this vertex.

In degree

In a directed graph G, the in degree of v denoted by in deg G (v) or deg ^-1_G (v), is the number of edges ending at v.

Out degree

In a directed graph G, the out degree of vertex of v of G denoted by out deg_G(v) or deg⁺_G (v), is the number of edges beginning at v.

Note:

(1) The sum of the in degree and out degree of a vertex is called the total degree of the vertex.

(2) A vertex with zero in degree is called a source and a vertex with zero out degree is called a sink.

Theorem: If G = (V, E) be a directed graph with e edges, then

Σ_vϵV deg⁺_G (v) = Σ_vϵV deg^-_G (v) = e

i.e., the sum of the outdegrees of the vertices of a diagraph G equals the sum of in degrees of the vertices which equals the number of edges in G.

Proof: Each edge has an initial vertex and a terminal vertex.

⇒ Each edge contributes one out degree to its initial vertex and one indegree to its terminal vertex.

Thus the sum of the indegrees and the sum of the out degrees of all vertices in a directed graph are same.

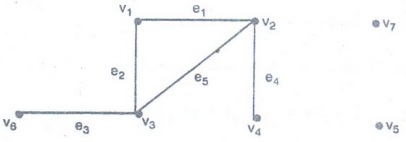
Example 10. Verify Σⁿ_i=1 deg⁺_G (v_i) = Σ ⁿ_i=1 deg^- (v_i) = |E| = e in the  following graph.

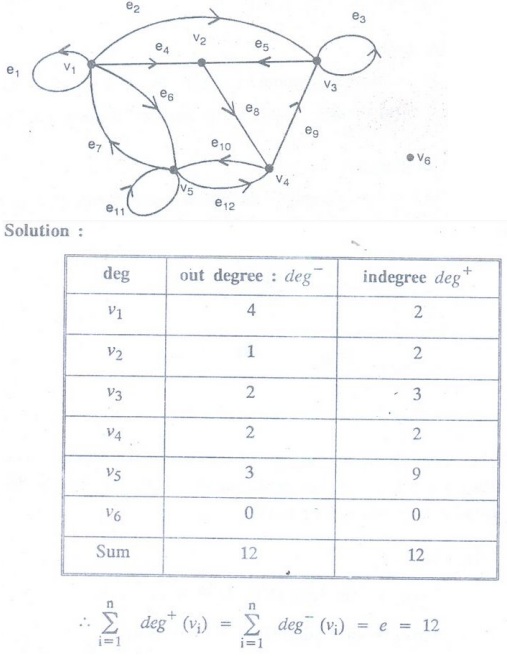
Example 11. What do the in-degree and the out-degree of a vertex in a directed graph modeling a round-robin tournament represent?

Solution: (deg⁺ (v), deg^- (v)) is the win-loss record of v.

Definition: Underlying undirected graph. The undirected graph that results from ignoring directions of edges is called the underlying undirected graph.

Example 12. Construct the underlying undirected graph for the graph with directed edges in the following figure.

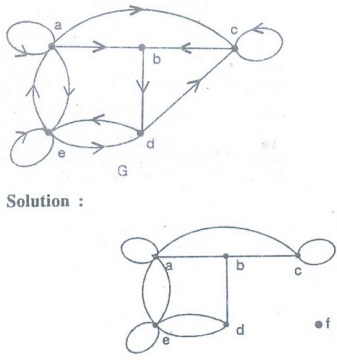
The minimum of all the degrees of the vertices of a graph G is denoted by δ (G), and the maximum of all the degrees of the vertices of G is denoted by ∆ (G).

In otherwords

δ (G) = min {deg (V) / VϵV (G)} and

∆ (G) = max {deg (V) / VϵV (G)}

d (V₁) = d (V₃) = 3

d (V₂) = d(V₄) = 4

d (V₅) = 1

δ (G) = 1

∆ (G) = 4

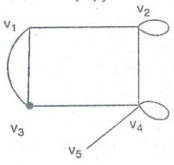
Clearly δ (G)  ≤  ∆ (G) = 4

If δ (G) = ∆ (G) = K  i.e., if each vertex of a graph G has degree K, then G is said to be K - regular graph of degree K.

d (V₁) = d (V₂) = d (V₃) = d (V₄) = 2

The given graph is 2-regular (or) regular graph of degree 2.

If G is a K-regular graph, then δ = 2 |E| / |V| = ∆

If V₁, V₂, V₃, ….  V_n are the n vertices of G, then the sequence (d₁, d₂, …, d_n), where d_i = deg (v_i) is the degree sequence of G.

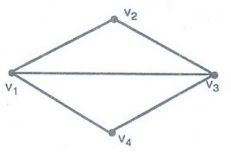
A degree sequence of G: (2, 2, 3, 5)

A degree sequence d = (d₁, d₂, …. d_n) is graphic if there is a simple undirected graph with degree sequence d.

Is there a graph with degree sequence (1, 3, 3, 3, 7, 6, 6). No, because the no. of vertices with odd degree is odd, a contradiction to corollary; the number of vertices of odd degree must be even.

A simple graph in which every pair of distinct vertices are adjacent is called a complete graph. If G has n vertices then the complete graph will be denoted by K_n.

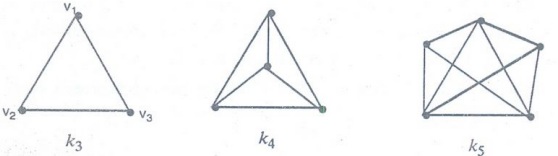
Example 13. Draw these graphs

(a) K₅       (b) K₆       (c) K₇

Solution :

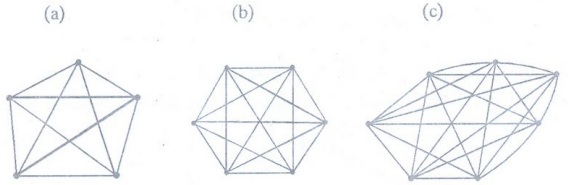
Example 14. Draw Graphs K_n for 1 ≤ n ≤4

Solution :

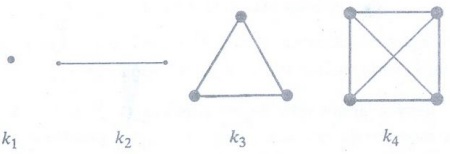
Example 15. What is the degree sequence of K, where n is a positive integer? Explain your answer.

Solution: Each of the n vertices is adjacent to each of the other n-1 vertices, so the degree sequence is n - 1, n - 1, ..., n - 1 (n terms)

Example 16. Determine whether each of these sequences is graphic. For those that are, draw a graph having the given degree sequence. (a) 5, 4, 3, 2, 1 (b) 3, 2, 2, 1, 0 (c) 1, 1, 1, 1, 1

Solution :

(a) No, (5+4+3+2+1=15) sum of degree is odd

(b) Yes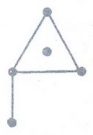  

(c) No, (1+1+1+1+1=5) sum of degrees is odd.

Example 17. How many vertices and how many edges of K_n?

Ans. n vertices, n (n - 1)/2 edges.

Example 18. Find the degree sequence of each of the following graphs (a) K₄ (b) K₅ (c) K₂

Solution :

(a) 3, 3, 3, 3

 (b) 4, 4, 4, 4, 4

(c) 1, 1

Definition: Cycle Graph

A cycle graph of order 'n' is a connected graph whose edges form a cycle of length 'n' and denoted by C_n.

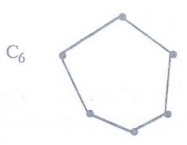
Note:

(1) In a graph a cycle that is not a loop must have length atleast 3, but there may be cycles of length 2 in a multigraph.

(2) A simple digraph having no cycles is called a cyclic graph.

(3) An cyclic graph cannot have any loops.

(4) The cycle C_n, n ≥ 3, consists of n vertices 1, 2, …, n and edges {1, 2}, {2, 3},... {n-1, n}

Example 19. Draw the graphs (a) C₃ (b) C₄ (c) C₅ (a) C₆, (e) C₈

Solution :

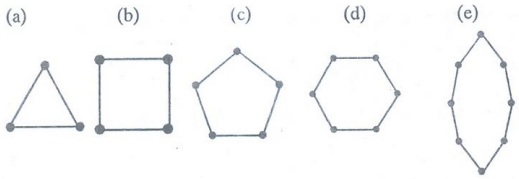
Example 20. How many vertices and how many edges do these graphs have (a) C_n (b) C₈ (c) Also find the degree sequence of C₄.

Solution :

(a) n vertices, n edges

(b) 8 vertices, 8 edges.

(c) 2, 2, 2, 2

Definition: Wheel Graph :

A wheel graph of order n is obtained by joining a new vertex called 'Hub' to each vertex of a cycle graph of order n 1, denoted by W_n.

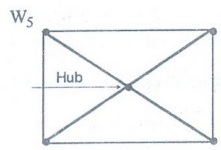
Note: We obtain the wheel W_n when we add an additional vertex to the cycle C_n, for n ≥ 3, and connect this new vertex to each of the n vertices in C_n, by new edges.

Example 21. Draw the graphs (a) W₃, (b) W₄ (c) W₅, (d) W₆, (e) W₇

Solution :

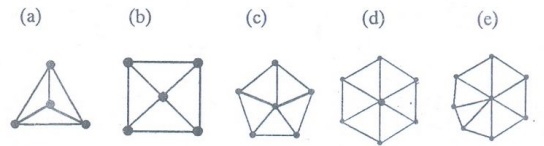
Example 22. How many vertices and how many edges do these graph have (a) W_n (b) W₅ also find the degree sequence of W₄

Solution :

(a) n + 1 edges, 2n edges

(b) 5+1 = 6 vertices, (2)(5) = 10 edges

(c) 4, 3, 3, 3, 3

Definition: n-Cubes :

The n-dimensional hypercube, or n-cube, denoted by Q_n; is the graph that has vertices representing the 2ⁿ bit strings of length n. Two vertices are adjacent if and only if the bit strings that they represent differ in exactly one bit position.

Example 23. Draw the graphs (a) Q₁      (b) Q₂        (c) Q₃

Solution :

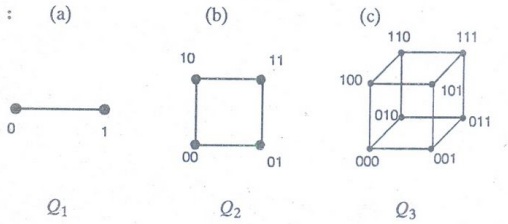
Example 24. How many vertices and how many edges do those graphs here?

(a) Q_n     (b) Q₃

Solution :

(a) 2ⁿ vertices, n 2^n-1 edges

(b) 2³ = 8 vertices, (3) (2²) = 12 edges

Example 25. Find the degree sequence of Q₃.

Solution: 3, 3, 3, 3, 3, 3

Regular graph:                [A.U N/D 2012]

A graph in which all vertices are of equal degree is called a regular graph.

If the degree of each vertex is r, then the graph is called a regular graph of degree r.

Note :

(1) Every null graph is regular of degree zero.

(2) The complete graph k_n of degree n - 1.

(3) If G has n vertices and is regular of degree r, then G has (½) r n edges.

Example 26. What is the size of an r-regular (p, q) graph?

Solution : By the definition of regularity of G,

we have deg_G (v₁) = r for all v₁ϵV(G)

But 2q = Σ deg_G (v₁)

= Σ r

= pr

q = pr/2

Example 27. Does there exists a 4-regular graph on 6 vertices if so construct a graph.

Solution: We know that q = pr/2 = (6)(4)/2 = 12

Four regular graph on 6 vertices is possible and it contains 12 edges.

Example 28. For which values of n are these graphs regular? (a) K_n (b) C_n (c) W_n (d) Q_n

Solution:

(a) For all n ≥1

(b) For all n ≥ 3

(c) For n = 3

(d) For all n ≥0

Example 29. How many vertices does a regular graph of degree four with 10 edges have?

Solution: Given

r = 4

q = 10

To find : p.

We know that 2q = pr

P =་ 2q/r

P = (2) (10)/4

p = 5

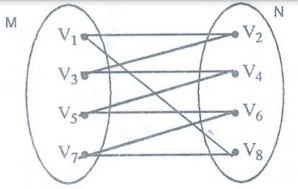
Definition Bipartite graph

A bipartite graph is an undirected graph whose set vertices can be partitioned into two sets M and N is such a way that each edge joins a vertex in M to a vertex in N and no edge joins either two vertices in M or two vertices in N.

here V = MUN ;       Μ∩Ν = ϕ

M = {V₁, V₃, V₅, V₇} ;        V = {V₂, V₄, V₆, V₈}

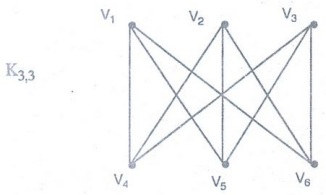
Definition: Complete Bipartite graph

A complete bipartite graph is a bipartite graph in which every vertex of M is adjacent to every vertex of N. The complete bipartite graphs that may be partitioned into sets M and N as above s.t M = m and |N| = n are denoted by K_{m, n}

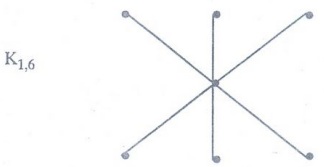
Definition: Star graph

Any graph that is K_{1, n} is called a star graph.

Example 30. Show that C₆ is a bipartite graph ?

Solution: The vertex set of C₆ can be partioned into the two sets

V₁ = {v₁, v₃, v₅} and V₂ = {v₂, v₄, v₆} and every edge of C₆ connects a vertex in V₁ and a vertex in V₂

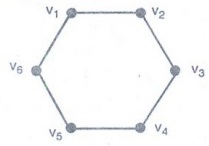
Hence C₆ is a bipartite graph.

Example 31. Is K₃ is bipartite?

Solution: No, the complete graph K₃ is not bipartite.

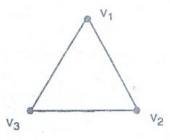
If we divide the vertex set of K₃ into two disjoint sets, one of the two sets must contain two vertices.

If the graph is bipartite, these two vertices should not be connected by an edge, but in K₃ each vertex is connected to every other vertex by an edge.

K₃ is not bipartite.

Example 32. How many vertices and how many edges of K_m,n graph have?

Solution: m + n vertices, mn edegs.

Example 33. Find the degree sequence of the following graph K_2,3

Solution: 3, 3, 2, 2, 2

Example 34. Show that the following graph G is bipartite.

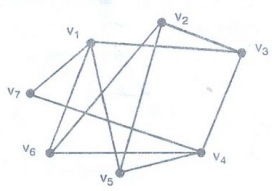
Solution: Graph G is bipartite since its vertex set is the union of two disjoint sets, {v₁, v₂, v₃} and {v₃, v₅, v₆, v₇}, and each edge connects a vertex in one of these subsets to a vertex in the other subset.

Example 35. For which values of m and n is K_m,n regular?

Solution: A complete bipartite graph K_m,n is not a regular it m ≠ n

→ If m = n then K_m,n is regular.

Example 36. Prove that a graph which contains a triangle can not be bipartite.

Proof: Atleast two of the three vertices must lie in one of the bipartite sets because there two are joined by edge, the graph can not be bipartite.

Example 37. Draw the complete bipartite graphs K_2,3, K_3,3 K_3,5 and K_2,6

Solution :

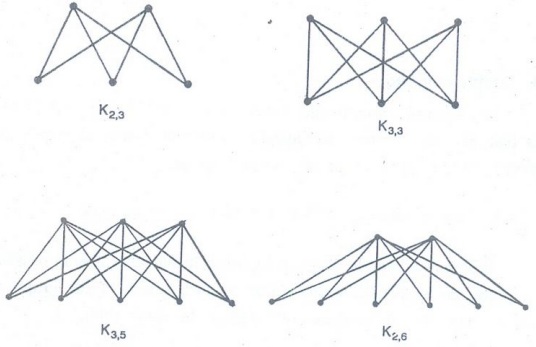
Example 38. Show that if G is a bipartite simple graph with v vertices and e edges, then e ≤ v²/4

Solution: Let G be a complete bipartite graph with v vertices.

Let v₁ and v₂ be the number of vertices in the partitions V₁ and V₂ of vertex set of G.

Since G is complete bipartite, each vertex in V₁ is joined to each vertex in V₂ by exactly one edge.

Thus G has v₁ v₂ edges when v₁ + v₂ = v

But we know that maximum value of v₁ v₂ subject to

v₁ + v₂ = v is v²/4

Thus the maximum number of edges in G is v²/4

ie. e ≤ v²/4

Graph coloring

The assign of colors to the vertices of G, one color to each vertex, so that adjacent vertices are assigned different colors is called the proper coloring of G or simply vertex coloring.

If G has n coloring, then G is said to be n-colorable.

Theorem: A simple graph is bipartite if and only if it is possible to assign one of two different colors to each vertex of the graph so that no two adjacent vertices are assigned the same color.

Proof: Let G = (V,E) is a bipartite simple graph. Then V = V₁UV₂, where V₁ and V₂ are disjoint sets and every edge in E connects a vertex in V₁ and a vertex in V₂.

If we assign one color to each vertex in V₁ and a second color to each vertex in V₂, then no two adjacent vertices are assigned the same color.

Suppose that it is possible to assign colors to the vertices of the graph using just wo colors.

→ No two adjacent vertices are assigned the same color.

Let V₁ be the set of vertices assigned one color and V₂ be the set of vertices assigned the other colour. Then, V₁ and V₂ are disjoint and V = V₁UV₂.

i.e., every edge connects a vertex in V₁ and a vertex in v₂ since no two adjacent vertices are either both in V₁ or both in V₂. Consequently, G is bipartite.

Job Assignment problem

A company receives 5 applications to fill 6 vacant positions. Applicant x₁ is qualified to fill positions P₁ and P₄. Applicant x₂ is qualified to fill positions P₁, P₂, P₃, P₄ and P₅.

Applicant x₃ is qualified to fill positions P₂ and P₄. Applicant x₄ is qualified to fill positions. P₂, P₃, P₄, P₅ and P₆. Applicant x₅ is qualified to fill positions P₂ and P₄.

The problem is: Is it possible to recruit all the applicants and assign a job for which he is qualified?

We introduce a graph model for this with a vertex representing an applicant or a job and if an applicant is qualified for a job then we introduce an edge between the corresponding vertices.

Now, the problem becomes, finding a matching in this graph which is incident with all the x j s.

Such a matching does not exist in the graph, since the neighbour set of x₁, x₃ and x₅ is the same set {P₂, P₄}, that is, the applicants x₁, x₃ and x₅ are qualified only for 2 jobs, P₂ and P₄. Thus one of the 3 applicants cannot be matched.

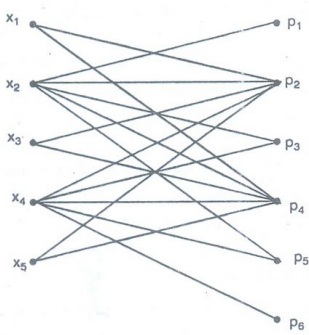
Hence we cannot recruit all the five applicants and assign a job for which they are qualified.

Local Area Networks :

In various computers in a building, such as minicomputers and personal computers, as well as peripheral devices such as printers and plotters, can be connected using a local area network.

Some of these networks are based on a star topology, where all devices are connected to a central control device.

Parallel processing :

Computers made up of many separate processors, each with its own memory, helps overcome the limitations of computers with a single processor.   

Parallel algorithms, which break a problem into a number of subproblems that can be solved concurrently, can then be devised to rapidly solve problems using a computer with multiple processors.

Definition: Subgraph

A subgraph of a graph G = (V,E) is a graph H = (W, F), where W≤V and F≤E. A subgroup H of G is a proper subgraph of G if H≠G.

Example 39. Draw two subgraph of K₅.

Solution:

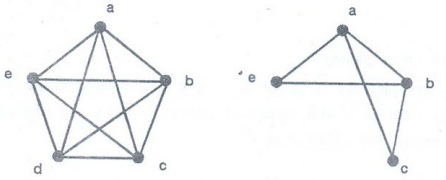
Example 40. How many subgraphs with atleast one vertex does K₃ have ?

Solution: 17

Definition: The union two simple graphs G₁ = (V₁, E₁) and G₂ = (V₂, E₂) is the simple graph with vertex set V₁ U V₂ and edge set E₁UE₂. The union of G₁ and G₂ is denoted by G₁ U G₂.

Example 41. Find the union of the graphs G₁ and G₂

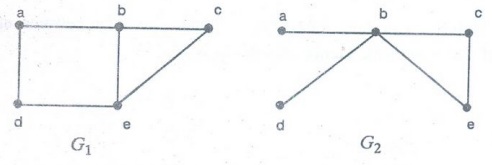
Solution : The vertex set of G₁ = {a, b, c, d, e}

The vertex set of G₂ = {a, b, c, d, f}

G₁UG₂ = {a, b, c, d, e, f}

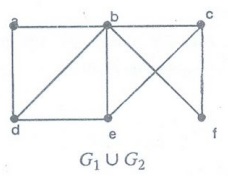
Definition: Complement

The complement  of G is defined as a simple graph with the same vertex set as G and value two vertices u and v are adjacent only when then are not adjacent in G.

Example 42. If the simple graph G has v vertices and e edges, how many edges does  have?

Solution:  have the edges.

= v (v-1) / 2e

Example 43. Show that if G is a simple graph with n vertices, then the union of G and  is K_n.

Solution: The union of G and  contains an edge between each pair of the n vertices. Hence this union is K_n.

EXERCISE 3.2

1. Can a simple graph exist with 15 vertices each of degree five?

[Ans. No. because the sum of the degree of the vertices cannot be odd.]

2. Find the number of vertices, the number of edges, and the degree of each vertex in the given undirected graph. Identify all isolated and pendant vertices.

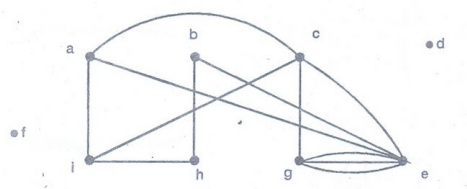
[Ans. v = 9, e = 12; deg (a) = 3, deg (b) = 2, deg (c) = 4, deg (d) = 0, deg(e) 6, deg (f) = 0; deg (g) = 4; deg(h) = 2; deg(i) = 3, d and ƒ are isolated.]

3. What does the degree of a vertex represent in a collaboration graph? What do isolated and pendant vertices represent?

[Ans. The number of colloaborators v has; someone who has never collaborated; someone who has just one collaborator.

4. What does the degree of a vertex represent in the acquaintanceship graph, where vertices represent all the people in the word? What do isolated and pendant vertices in this graph represent ? In one study it was estimated that the average degree of a vertex in this graph is 1000. What does this mean in terms of the model ?

5. Determine whether the graph is bipartite.

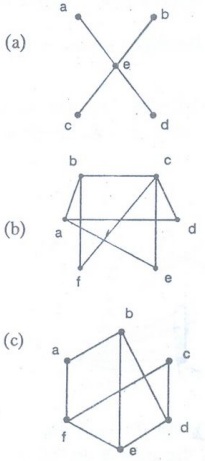
6. For which values of n are these graphs bipartite?

(a) K_n     (b) C_n     (c) W_n      (d) Q_n

7. Draw the mesh network for interconnecting nine parallel processors.

 [Ans. 

9. Show that every pair of processors in a mesh network of n = m² processors can communicate using O (√n) = O (m) hops between directly connected processors.