Discrete Mathematics: Unit II: Combinatorics
Generating Functions
Combinatorics - Discrete Mathematics
The generating function for the sequence a0, a1, … ak, … of real numbers is the infinite series.
Generating
Functions
Definition: Generating Function
The
generating function for the sequence a0, a1, … ak,
… of real numbers is the infinite series.

Example 1: What is the generating
function for the sequence 1, 1, 1, 1, 1?
Solution:
The generating function of 1, 1, 1, 1, 1, is
1
+ x + x2 + x3 + x4
(i.e.,)
1 + x + x2 + x3 + x4 = x5-1/ x-1
when x ≠ 1.
Consequently,
G (x) = x5-1/ x-1 is the G.F. of the sequence 1, 1, 1, 1, 1.
Example 2 Find the generating
function for the finite sequence 2, 2, 2, 2, 2.
Solution:
The generating function of 2, 2, 2, 2, 2 is
2
+ 2x + 2x2 + 2x3 + 2x4
(i.e.,)
2 + 2x + 2x2 + 2x3 + 2x4
=
2 [1 + x + x2 + x3 + x4] = 2 [x5-1/
x-1] when x ≠ 1.
Consequently,
G (x) = 2 [x5-1/ x-1] is the G.F. of the sequence 2, 2, 2, 2, 2.
Example 3 Find the values of the
extended binomial coefficients

Example 4 Find the generating
function for (1 + x)-n, where n is a positive integer.
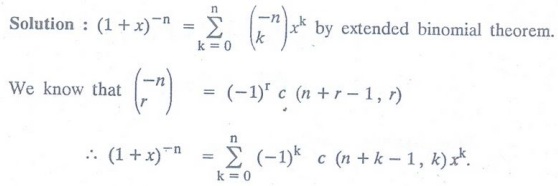
Example 5: Find the generating
function for the sequence 1, a, a2,... where a is a fixed constant.
Solution:
The generating function of 1, a, a2, … is
1+
ax + a2x2 + a3x3 + ….
Let
G(x) = 1 + ax + a2x2 + a3x3 + … (1)
G(x)
- 1 = ax + a2x2 + c3x3 + ...
=
ax [1 + ax + a2x2 + ...]
G(x)-1/
ax = 1 + ax + a2x2 + ...
=
G(x) by (1)
G(x)
- 1 = ax G(x)
G(x)
- ax G(x) = 1
G(x)
[1 - ax] = 1
G(x)
= 1 / 1-ax
which
is the required G.F.
Example 6 Find the generating
function for the sequence 1, 4, 16, 64, 256, …
Solution:
The generating function of 1, 4, 42, 43, 44, …
is
1+
4x + 42x2 + 43x3 + 44x4
+ …
Let
G (x) = 1+ 4x + 42x2 + 43x3 + 44x4
+ …
From
Example 5. G (x) = 1/1-4x
Note:

Example 7: Find a closed form for
the generating function of 0, 0, 1, 1, 1, ...
Solution:
We know that

Example 8: Find a closed form for
the generating function of 3, -3, 3, -3, 3, -3, ...

Example 9: Find a closed form for
the generating function

Example
10: Find a closed form for the generating function an = 5 for all n
= 0, 1, 2, ….
Solution:
Given: an = 5 for all n = 0, 1, 2, ….
(i.e.,) a0 = 5, a1 = 5,
a2 = 5, a3 = 5, ...
(i.e.,)
5, 5, 5, 5, ...
The
generating function of 5, 5, 5, 5,
5
+ 5x + 5x2 + …. = 5 [ 1 + x + x2 + ... ]
=
5[1-x]-1
=
5/1-x
G
(x) = 5/1-x which is the G.F. of the given sequence.
Example 11: Find a closed form for
the generating function for the sequence {an} when an = 3n
for all n = 0, 1, 2, ...
Solution:
Given: an = 3n, n =
0, 1, 2, ...
an
=30, a1 = 3, a2 = 32, a3
= 33, ….
(i.e.,) 1, 3, 32, 33,
...
The
generating function of 1, 3, 32, 33, ... is
G(x)
= 1 + 3x + 32 x2 + 33 x3 +...
=
(1-3x)-1
=
1 / 1-3x which is the G.F of the given sequence.
Example 12 In how many different
ways can eight identical cookies be distributed among three distinct children
if each child receives atleast two cookies and no more than four cookies ?
Solution:
Each child receives atleast two but no more than four cookies, for each child
there is a factor equal to (x2 + x3 + x4) in
the generating function for the sequence {cn}, where cn
is the number of ways to distribute n cookies. For three children, the
generating function is
(x2
+ x3 + x4)3.
We
need the coefficient of x8 in this product. Since x8 terms in the expansion
correspond to the ways that three terms can be selected, with one from each
factor, that have exponents adding up to 8.
Moreover
the the exponents of the term from the first, second and third factors are the
numbers of cookies the first, second, and third children receive, respectively.
This
shows that the coefficient equals 6. Hence, there are six ways to distribute
the cookies so that each child receives atleast two, but no more than four
cookies.
Example 13: Use generating
functions to solve the recurrence relation an = 3an-1 + 2
with the initial condition a0 = 1.


Example 14: Use generating
functions to solve the recurrence relation. an+2 - 2an+1 +
an = 2n with initial condition a0 = 2, a1
= 1.


Example 15: Find the co-efficient
of x10 in (1 + x5 + x10 + x15 +...)3.
Solution:
We know that
(1
+ x5 + x10 + x15 +...)3 = [(1 – x5)−1]3
= (1 – x5)−3
=
Σ c (3 + r−1, r) x5r
To
find the coefficient of x10, put 5r = 10
⇒r = 2
.
The required coefficient is c (3+2-1, 2) = c (4, 2)
=
4c2
=
6
Example 16: Find the coefficient of
x10 in (x3 + x4 + x5 +...)3.
Solution:
Given: (x3 + x4 + x5 +...)3 = x9
(1 + x + x2 + ...)3
=
x9 [(1-x)-1]3
=
x9 (1-x)-3
=
Σ c (3+r-1, r) xr
=
Σ c (3+r-1, r), x9+r
To
find the coefficient of x10
(i.e.,)
9+r = 10
r
= 1
The
required coefficient is c (3+1-1, 1) = c (3, 1)
=3c1
=
3
Example 17 Find the coefficient of
x18 in (x + x2 + x3 + x4 + x5)
(x2 + x3 + x4 + ...)5.
Solution:
We know that = (x + x2 + x3 + x4 + x5)
(x2 + x3 + x4 + ...)5
=
x (1 + x + x2 + x3 + x4 ) x10 (1 +
x + x2 + ...)5
=
x11 (1 + x + x2 + x3 + x4 ) [(1 - x
)1]5
=
x11 [1 – x5/1 - x ] (1 - x )-5
=
x11 (1 – x5 ) (1 -
x )-6
=
(x11 – x16 ) (1 -
x )-6
=
(x11 – x16 ) Σ c (6 + r – 1, r) xr
=
Σ c (6 + r – 1, r) x11+r - Σ c (6 + r – 1, r) x16+r
Hence
the coefficient of x18 is c (6 +7-1, 7) - c (6+2-1, 2)
=
c (12, 7) - c (7, 2)
=
792 - 21
=
771
Example 18: Using generating
function, prove the relation c (n, r) = c (n-1, r) + c (n-1, r- 1)
[Pascal's identity]
Solution:
We know that c (n, r) is the coefficient of xr in (1 + x)n.
But
(1+x)n = (1+x)n-1 + x (1+x)n-1 …..(1)
The
coefficient of xr in (1 + x)n-1 is c (n − 1, r)
The
coefficient of xr in x(1 + x)n-1 is c (n − 1, r − 1)
This
shows that
c
(n, r) = c (n-1, r) + c (n−1, r - 1)
[
`.` the coefficient of xr in L.H.S. of (1) is equal to the sum of coefficients
of xr of the two terms in the R.H.S. of (1)]
Example 19: Use generating
functions to show that

Example 20: Use generating
functions to find an explicit formula for the Fibonacci numbers.

EXERCISE
2.8
1.
Find the generating function for the finite sequence 2, 2, 2, 2, 2, 2.
2.
Find a closed form for the generating function for each of these sequences.
(a)
0, 2, 2, 2, 2, 2, 2, 0, 0, 0, 0, 0 ...
(b)
0, 0, 0, 1, 1, 1, 1, 1, 1, ….
(c)
2, 4, 8, 16, 32, 64, 128, 256, ...
3.
Find a closed form for the generating function for the sequence {an},
where an = 2 for n = 3, 4, 5 and a0 = a1 = a2
= 0
4.
Find a closed form for the generating function for the sequence {an},
where an = 2n+ 3 for all n 0, 1, 2, …
5.
Find a closed form for the generating function for the sequence
{an},
where an = (8n) for all n = 0, 1, 2, ..
6.
Find a closed form for the generating function for the sequence {an},
where an = (n+4n) for all n = 0, 1, 2, ...
7.
Find the coefficients of x10 in the power series of each of these functions.
(x4
+ x5 + x6) (x3 + x4 + x5
+ x6 + x7) (1 + x + x2 + x3 + x4
+...)
8.
Find the coefficients of x10 in the power series of each of these functions.
(x2
+ x4 + x6 + x8 + ...) (x3 + x6
+ x9 + ….
) (x4 + x8 + x12 + ...)
9.
Find the coefficients of x10 in the power series of each of these functions.
(1
+ x2 + x4 + x6 + x8 + ...) (1 + x4
+ x8 + x12 + ...)
(1
+ x4 + x8 + x12 + ...) (1 + x6 + x12
+ x18 + ...)
10.
Find the coefficient of x10 in the power series of each of these functions.
(a)
1/(1 - 2x)
(b)
1/ (1-x)3
(c)
x4 / (1 − 3x)3
11.
Use generating functions to determine the number of different ways 10 identical
balloons can be given to four children if each child receives atleast two
balloons.
12.
In how many ways can 25 identical donuts be distributed to four police officers
so that each officer gets atleast three but no more than seven donuts?
13.
Use generating functions to determine the number of different ways 15 identical
stuffed animals can be given to six children so that each child receives
atleast one but no more than three stuffed animals.
14.
Give a combinatorial interpretation of the coefficient of x4 in the
expansion (1 + x + x2 + x3 +...)3. Use this
interpretation to find this number.
15.
If G (x) is the generating function for the sequence {ak}, what is
the generating function for each of these sequences?
(a)
0, 0, 0, a3, a4, a5 … (assuming that terms
follows the pattern of all but the first three terms)
(b)
a0, a0 + a1, a0 + a1 + a2,
a0 + a1 + a2 + a3, …
16.
Use generating functions to solve the recurrence relation
ak
= 5ak-1 - 6ak-2 with initial conditions a0 = 6
and a1 = 30.
17.
Use generating functions to solve the recurrence relation
ak
= 4ak-1 -4аk-2 + k2 with initial conditions a0 = 2 and a1
= 5.
18.
Find a closed form of the exponential generating function for the sequence {an}
where
(a)
an = 2, (b) an = 3n, (c) an = n + 1
19.
Find the sequence with each of these functions as its exponential generating
function.
(a)
f(x) = e -x,
(b)
f(x) = 3x2x
(c)
f(x) = e -2x - (1/(1-x))
ANSWERS
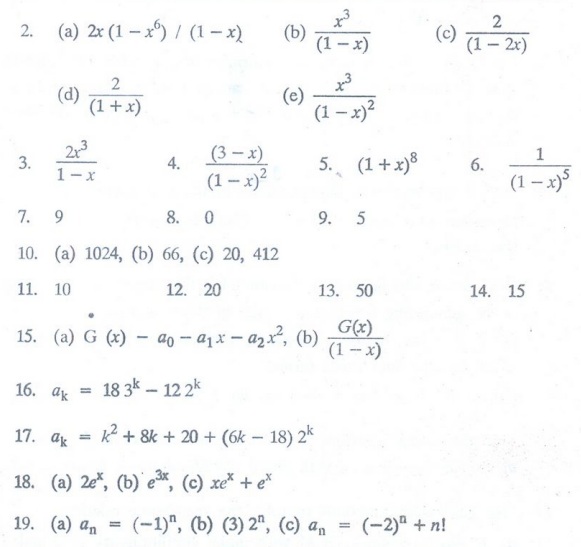
Discrete Mathematics: Unit II: Combinatorics : Tag: : Combinatorics - Discrete Mathematics - Generating Functions
Related Topics
Related Subjects
Discrete Mathematics
MA3354 3rd Semester CSE Dept | 2021 Regulation | 3rd Semester CSE Dept 2021 Regulation
