Artificial Intelligence and Machine Learning: Unit I(e): Adversarial search
Games with Chance
Adversarial search - Artificial Intelligence and Machine Learning
Games with a certain element of chance are often more interesting than those without chance, and many games involve rolling dice, tossing a coin or something similar.
Games
with Chance
Games
with a certain element of chance are often more interesting than those without
chance, and many games involve rolling dice, tossing a coin or something
similar.
- In
the real world many situation infront of us are unpredictable. It is also
observed in many games.
Example: Dice rolling, backgammon.
-
Some time, in the game, imperfect information is available.
Example: Cards, dominose, etc.
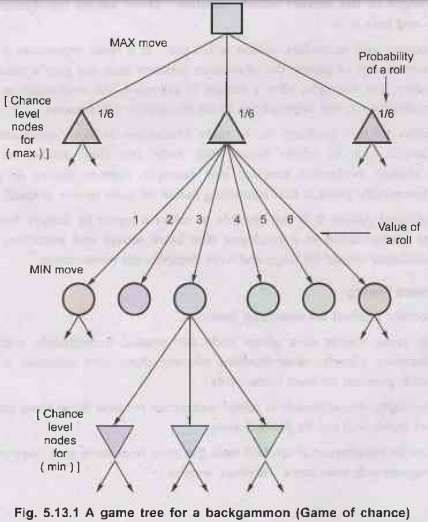
- In
game with chance, we can introduce probabilities to our search diagrams and
calculate minimax solutions as in the normal games.
- We
add 1 more level in game tree i.e. the level of chance nodes.
-
Chance nodes have as many successors as outcomes of the random element.
-
Minimax with element of chance
1) di
(i = 1, ..., n) - Outcomes from the chance nodes.
2) P
(di) - Probability of di;
3) S
(N, di) - Moves from position N for outcome di;
4)
If N is MAX : Utility (N) = Σni=1 P(di)
maxs ε S(N, di) utility (s)
5)
If N is MIN:
Utility
(N) = Σni=1 P(di) maxs
ε S(N, di) utility (s)
-
The utility is not computed by using just the terminal values. Therefore values
assigned to win, loss and draw affect the choice of moves.
-
Time complexity increases (n outcomes from the chance nodes) to O (bd nd).
-
Alpha-Beta pruning is more complicated in this game trees.
Artificial Intelligence and Machine Learning: Unit I(e): Adversarial search : Tag: : Adversarial search - Artificial Intelligence and Machine Learning - Games with Chance
Related Topics
Related Subjects
Artificial Intelligence and Machine Learning
CS3491 4th Semester CSE/ECE Dept | 2021 Regulation | 4th Semester CSE/ECE Dept 2021 Regulation
