Formal Representation of a Game as a Problem

Formal Representation of a Game as a Problem

A Game is Essentially a Kind of a Search Problem!

Game is formally defined with following four components: -

1. The initial state, which includes the board position and identifies the player to move.

2. A successor function, which returns a list of (move, state) pairs, each indicating a legal move and the resulting state.

3. A terminal test, which determines when the game is over. States where the game has ended are called as terminal states.

4. A utility function (also called an objective function or payoff function), which gives a numeric value for the terminal states. In chess, the outcome is a win,   loss or draw, with values +1, - 1, or Ө. Some game have a wider variety of possible outcomes; the payoffs in backgammon range from + 192 to -192.

Game Playing Strategies

A players's strategy in a game is a complete plan of action for whatever situation might arise. It is a complete algorithm for playing the game, telling a player what to do for every possible situation throughout the game.

A pure strategy provides a complete definition of how a player will play a game. In perticular, it determines the move a player will make for any situation they could face. A player's strategy set, is the set of pure strategies available to that player.

A mixed strategy is an assignment of a probabiblity to each pure strategy. This allows for a player to randomly select a pure strategy. Since probabilities are continuous, there are infinitely many mixed strategies available to a player, even if their strategy set is finite.

A mixed stretegy for a player is a probability distribution, on the set of his pure strategies.

• Games can be classified as either a single-person playing or multiperson playing.

• For example, Rubik's cube and 8-tile puzzle are single person games. For solving such problems strategies like best-first or A* algorithm can be used. These strategies help in identifying paths in a clear fashion.

• While for solving problem, where two person play a game like chess or checkers etc., cannot be solved by best-first search or A* algorithms. As here each player tries to outsmart the opponent. Each has their own way of evaluating the situation.

• The basic characteristic of the strategy must be look ahead in nature i.e., explore the tree for two or more levels downwards and choose the optimal one. The basic methods available for game playing are -

i) Minimax strategy

ii) Minimax strategy with alpha-beta cutoffs.

• A Two Player Strategy Table.

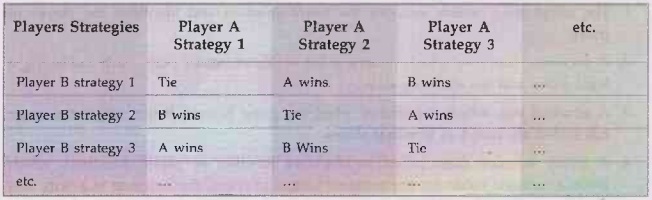
• It is a techniques which always leads to superior solution than any other strategy, as opponent is playing in perfect manner.

• Roughly speaking, an optimal strategy leads to outcomes that are at least as good as any other strategy when one is playing an infallible opponent.

Mini-Max Value

The minimax value for a given game tree is determined by optimal strategy by evaluating minimax value of each node.

Mini-Max Theorem

Players adopt those strategies which will maximize their gains, while minimizing their losses. Therefore the solution is, the best each player can do for him/herself in the face of opposition of the other player.

Determining Optimal Strategy

1. Given a game tree the optimal strategy can be determined by examining the minimax value of each node.

2. The minimax value of a node is the utility (for player called MAX) of being in the corresponding state, assuming that both players play optimally from this stage to the end of the game.

3. The minimax value of a terminal state is just its utility.

4. Given a choice, MAX will perfer to move to a state of maximum value, whereas MIN prefers a state of minimum value.

Game Tree

The initial state and the legal moves for each side, define the game tree for the game.

• Description of the game tree [Refer Fig. 5.9.1]

1. Root node -

Represents board configuration and decision, required as to what is the best singlenext move.

If my turn to move, then the root is labeled a MAX node indicating it is my turn;

Otherwise it is labeled a MIN, node to indicate it is my opponent's turn.

2. Arcs -

Represent the possible legal moves for the player that the arcs emanate from.

3. At each level, the tree has nodes that are all MAX or all MIN.

4. Since moves alternate, the nodes at level 'ï' are of opposite kind from those at level i + 1.

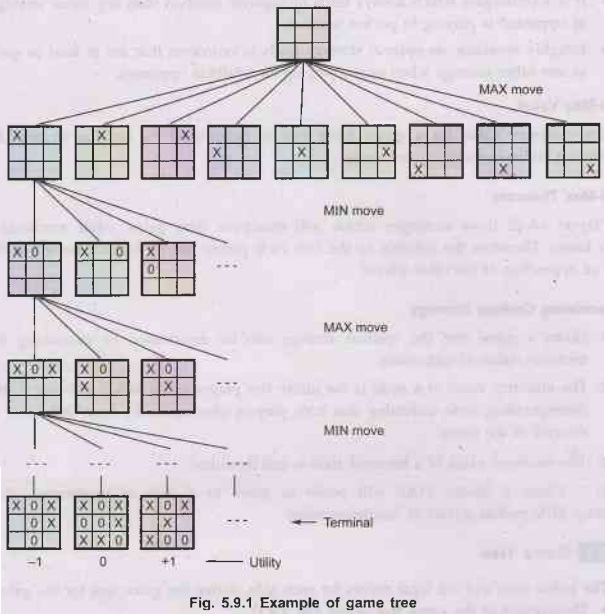
1. Above is a partial tree for the game of tic-tac-toe. T

2. The top node (root) is the initial state and MAX (player 1) moves first, placing X in an empty square.

3. The rest of the search tree shows alternate moves for MIN (player 2) and MAX.

4. Terminal states are assign utilities according to the rules of game.