Digital Principles and Computer Organization: Unit II (a): Synchronous Sequential Logic
Flip-Flops
Synchronous Sequential Logic - Digital Principles and Computer Organization
Latches and flip-flops are the basic building blocks of the most sequential circuits.The main difference between latches and flip-flops is in the method used for changing their state.
Flip-Flops
AU :May-03,04,05,06,07,08,10,15,19, Dec.-03,04,06,08,09,10,14,15,16,18
Latches Vs Flip-Flops
• Latches and flip-flops are the basic
building blocks of the most sequential circuits.
• The main difference between latches
and flip-flops is in the method used for changing their state.
• A simple latch forms the basis for the
flip-flop.
• Latches are controlled by enable signal, and
they are level triggered, either positive level triggered or negative level
triggered.
• The output state is free to change
according to the S and R input values, when active level is maintained at the
enable input.
• Flip-flops are pulse or clock edge
triggered instead of level triggered.
Level and Edge Triggering
Level Triggering
• In the level triggering, the output
state is allowed to change according to input(s) when active level (either
positive or negative) is maintained at the enable input.
• There are two types of level triggered
latches :
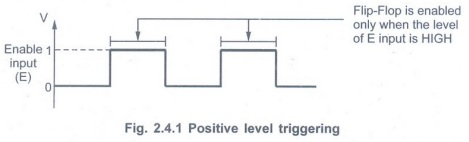
• Positive level triggered: The
output of flip-flop responds to the input changes only when its enable input is
1 (HIGH).
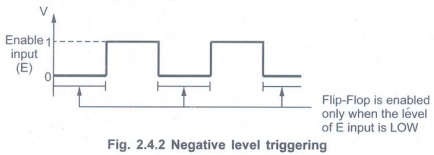
• Negative level triggered: The
output of flip-flop responds to the input changes only when its enable input is
0 (LOW).
Edge Triggering
•In the edge triggering, the output
responds to the changes in the input only at the positive or negative edge of
the clock pulse at the clock input.
• There are two types of edge
triggering.
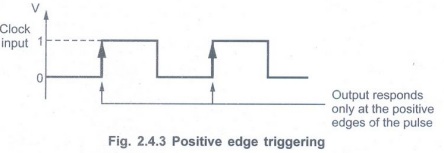
• Positive edge triggering: Here,
the output responds to the changes in the input only at the positive edge of
the clock pulse at the clock input.
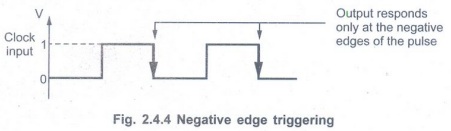
• Negative edge triggering: Here,
the output responds to the changes in the input only at the negative edge of
the clock pulse at the clock input.
SR Flip-Flop
Positive Edge Triggered SR Flip-Flop
•The Fig. 2.4.5 shows the positive edge
triggered clocked SR flip-flop.
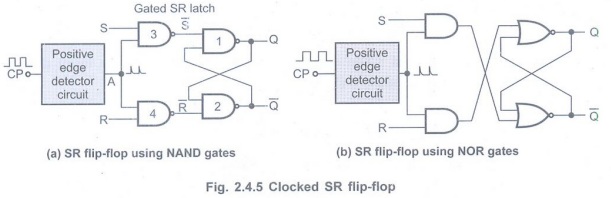
• The circuit is similar to SR latch
except enable signal is replaced by the Clock Pulse (CP) followed by the
positive edge detector circuit.
•The edge detector circuit is a
differentiator.
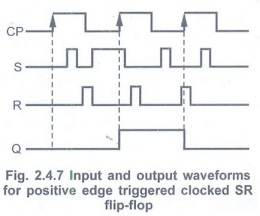
• The Fig. 2.4.7 shows input and output
waveforms for positive edge triggered clocked SR flip-flop.
• The circuit output responds to the S
and R inputs only at the positive edges of the clock pulse. At any other
instants of time, the SR flip-flop will not respond to the changes in input.
The Fig. 2.4.6 shows the logic symbol
and truth table of clocked SR flip-flop.
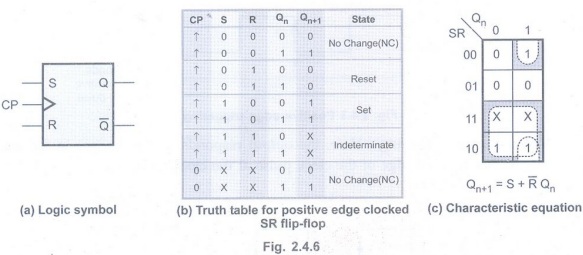
Case 1:If S = R = 0 and the clock pulse is applied, the output do not change, i.e. Qn+1= Qn. This is indicated in the first row of the truth table.
Case 2:If
S = 0, R = 1 and the clock pulse is applied, Qn+1= 0. This is
indicated in the second row of the truth table.
Case 3:If
S =1, R=0 and the clock pulse is applied,Qn+1= 1. This is indicated
in the third row of the truth table.
Case 4:
If S = R = 1 and the clock pulse is applied, the state of the flip-flip is
undefined and therefore is indicated as indeterminate in the fourth row of the
truth table.
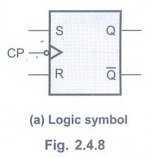
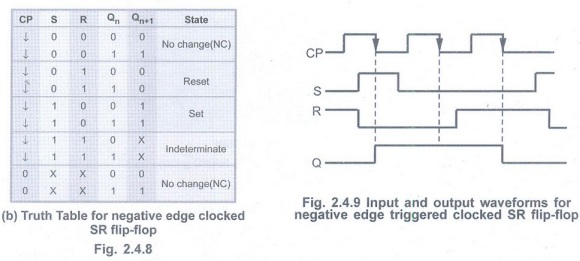
Negative Edge Triggered SR Flip-Flop
• In the negative edge triggered SR
flip-flop, the negative edge detector circuit is used and the circuit output
responds at the negative edges of the clock pulse.
• The Fig. 2.4.8 and Fig. 2.4.9 shows
the logic symbol, truth table, and input and output waveforms for negative edge
triggered SR flip-flop.
• The bubble at the clock input
indicates that the flip-flop is negative edge triggered.
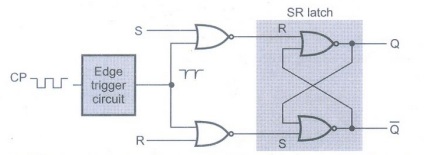
Example 2.4.1
Realize SR flip-flop using NOR gates.
Solution :
D Flip-Flop
• The Fig. 2.4.11 shows the logic
diagrams of D flip-flop.
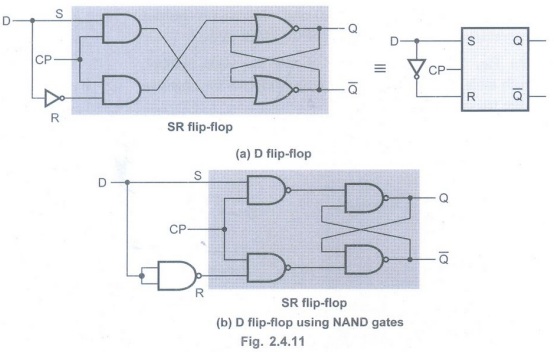
• The basic building block of D
flip-flop is a SR flip-flop.
• The SR flip-flop has two data inputs S
and R.
• The S input is made high to store 1 in
the flip-flop and R input is made high to store 0 in the flip-flop.
• When both inputs are same the output
either does not change or it is invalid (Inputs → 00, no change and inputs →
11, invalid).
• In many practical applications, these
input conditions are not required.
• These input conditions can be avoided
by making them complement of each other. This modified SR flip-flop is known as
D flip-flop.
• The D input goes directly to the S
input, and its complement is applied to the R input. Due to these connections,
only two input conditions exists, either S = 0 and R = 1 or S = 1 and R = 0.
Truth Table
• The truth table for D flip-flop
consider only these two conditions and it is as shown in the Fig. 2.4.12 (b).
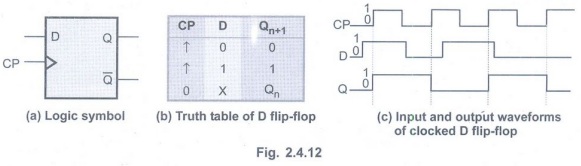
• Qn+1 function follows D
input at the positive going edges of the clock pulses. Hence the characteristic
equation for D flip-flop is Qn+1= D.
• The output Qn+1is delayed
by one clock period. Thus, D flip-flop is also known as delay flip-flop.
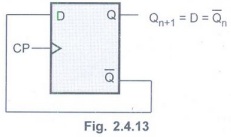
• If we connect the ![]() output of
D flip-flop to its D input as shown in the Fig. 2.4.13, the output of D
flip-flop will change either from 0 to 1 or from 1 to 0 at every positive edge
of the D flip-flop.
output of
D flip-flop to its D input as shown in the Fig. 2.4.13, the output of D
flip-flop will change either from 0 to 1 or from 1 to 0 at every positive edge
of the D flip-flop.
Such change in the output is known as
toggling of the flip-flop output.
Negative Edge Triggered D Flip-Flop
• In case of negative edge triggering,
the output is sensitive at the negative edge of the clock input.
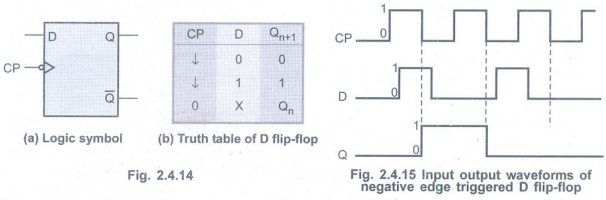
• The Fig. 2.4.14 shows the logic symbol
and truth table for negative edge triggered D flip-flop.
• Fig. 2.4.15 shows input and output
waveforms for negative edge triggered D flip-flop.
• The bubble at the clock input
indicates that the flip-flop is negative edge triggered.
Example 2.4.2
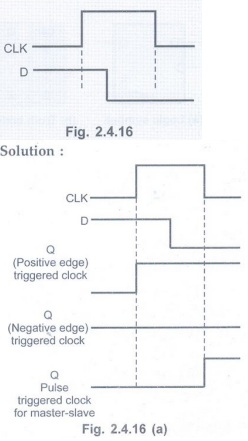
The D input and a single clock pulse are shown in Fig. 2.4.16. Compare the
resulting Q outputs for: Positive edge triggered flip-flop, negative edge
triggered flip-flop and pulse triggered master-slave flip-flops. The flip-flops
are initially RESET.AU: Dec.-04, Marks 3
JK Flip-Flop
The uncertainty in the state of an SR
flip-flop when S = R = 1 can be eliminated by converting it into a JK
flip-flop.
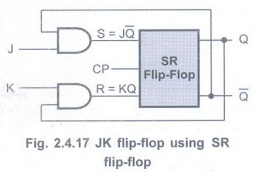
The data inputs are J and K which are
AND end with Q and ![]() , respectively, to obtain S and R inputs, as shown in the
Fig. 2.4.17. Thus,
, respectively, to obtain S and R inputs, as shown in the
Fig. 2.4.17. Thus, ![]() and R = K.Q.
and R = K.Q.
Operation of JK flip-flop
Case 1 :
J = K = 0
When J = K = 0, S = R = 0 and according
to truth table of SR flip-flop there is no change in the output.
When inputs J = K = 0, output does not
change.
Case 2:
J= 1 and K = 0
Q = 0, ![]() =1: When J=1,K=0 and
Q=0,S=1 and R=0.According to truth table of SR flip-flop it is set state and
the output Q will be 1.
=1: When J=1,K=0 and
Q=0,S=1 and R=0.According to truth table of SR flip-flop it is set state and
the output Q will be 1.
Q = 1, ![]() =0: When J = 1, K = 0
and Q = 1, S = 0 and R = 0. Since SR = 00, there is no change in the output and
therefore, Q = 1 and
=0: When J = 1, K = 0
and Q = 1, S = 0 and R = 0. Since SR = 00, there is no change in the output and
therefore, Q = 1 and ![]() = 0.
= 0.
The inputs J = 1 and K = 0, makes Q = 1,
i.e. set state.
Case 3:
J= 0 and K = 1
Q = 0, ![]() = 1: When J = 0, K = 1
and Q = 0, S = 0 and R = 0. Since SR there is no change in the output and
therefore, Q = 0 and
= 1: When J = 0, K = 1
and Q = 0, S = 0 and R = 0. Since SR there is no change in the output and
therefore, Q = 0 and ![]() = 1.
= 1.
Q = 1, ![]() = 0: When J 0, K = 1
and Q = 1, S = O and R = 1. According to truth table of SR flip-flop it is a
reset state and the output Q will be 0.
= 0: When J 0, K = 1
and Q = 1, S = O and R = 1. According to truth table of SR flip-flop it is a
reset state and the output Q will be 0.
The inputs J = 0 and K = 1, makes Q = 0,
i.e., reset state.
Case 4: J = K = 1
Q = 0, ![]() = 1: When J = K = 1
and Q = 0, S = 1 and R=0.According to truth table of SR flip-flop it is a set
state and the output Q will be 1.
= 1: When J = K = 1
and Q = 0, S = 1 and R=0.According to truth table of SR flip-flop it is a set
state and the output Q will be 1.
Q = 1, ![]() = 0: When J = K = 1
and Q = 1, S = 0 and R = 1. According to truth table of SR flip-flop it is a
reset state and the output Q will be 0.
= 0: When J = K = 1
and Q = 1, S = 0 and R = 1. According to truth table of SR flip-flop it is a
reset state and the output Q will be 0.
The input J = K = 1, toggles the
flip-flop output.
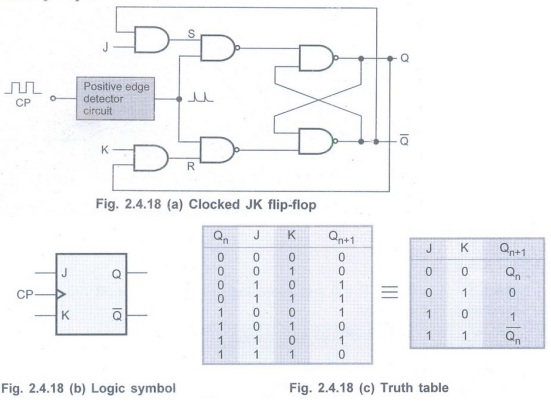
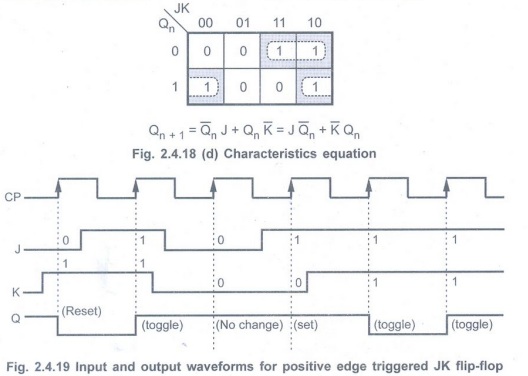
• Fig. 2.4.18 shows the logic symbol,
truth table and timing diagram of positive edge triggered JK flip-flop.
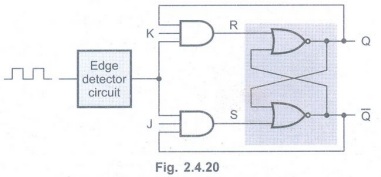
Example 2.4.3
Construct a clocked JK flip-flop which is triggered at the positive edge of
the clock pulse from a clocked SR flip-flop consisting of NOR gates.
Solution :
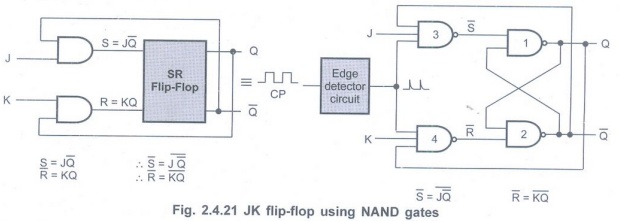
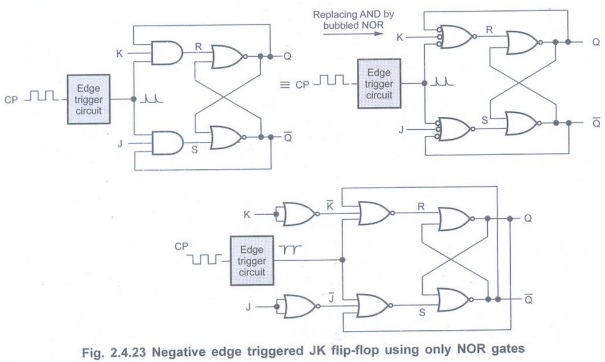
JK Flip-Flop using
NAND Gates
• The Fig. 2.4.21 shows the modified
circuit of JK flip-flop which has only NAND gates.
Race-around
Condition
• In JK flip-flop, when J = K = 1, the
output toggles (output changes either from 0 to 1 or from 1 to 0).
• Consider that initially Q = 0 and J = K
= 1. After a time interval At equal to the propagation delay through two NAND
gates in series, the output will change to Q = 1 and after another time
interval of At the output will change back to Q=0. This toggling will continue
until the flip-flop is enabled and J = K = 1. At the end of clock pulse the
flip-flop is disabled and the value of Q is uncertain. This situation is
referred to as the race-around condition. This is illustrated in Fig. 2.4.22.
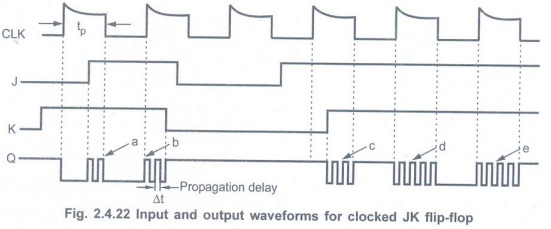
This condition exists when tp
≥ ∆t. Thus by keepingtp ≥ ∆t we can avoid race
around condition.
• We can keep tp ≥ ∆t by
keeping the duration of edge less than ∆t.
• A more practical method for overcoming
this difficulty is the use of the Master-Slave (MS) configuration.
Example 2.4.4
Realize a JK flip-flop using only NOR gates.
Solution :
Master-Slave SR Flip-Flop
• A master-slave flip-flop constructed
from two flip-flops.
• One circuit serves as a master and the
other as a slave and the overallcircuit isreferred to asamaster-slave
flip-flop.
• Fig. 2.4.24 shows SR
master-slave flip-flop
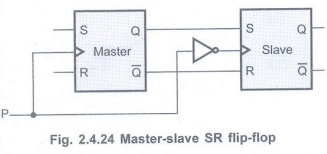
• It consists of a master flip-flop, a
slave flip-flop and an inverter.
• Both the flip-flops are positive level
triggered, but inverter connected at the clock input of the slave flip-flop
forces it to trigger at the negative level.
• The output state of the master
flip-flop is determined by the S and R inputs at the positive edge of the clock
pulse.
• The output state of the master is then
transferred as an input to the slave flip-flop. The slave flip-flop uses this
input at the negative edge of the clock pulse to determine its output state.
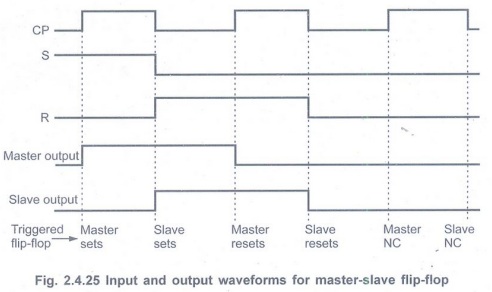
• Fig. 2.4.25 illustrates the operation
of the master-slave flip-flop.
Master-Slave D Flip-Flop
• Fig. 2.4.26 shows the block diagram of
master-slave D flip-flop. It consists of
clocked D flip-flop as a master and
another clocked D flip-flop as a slave.
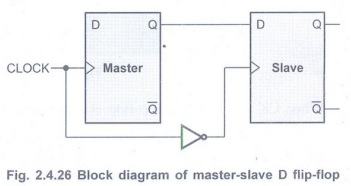
• Both the flip-flops are positive level
triggered, but inverter connected at the clock input of the slave flip-flop
forces it to trigger at the negative level.
• D input is transferred to the master at
the positive edge of the clock pulse and the same is copied by the slave and
therefore appears at the output Q of the slave flip-flop at the negative going
edge of the clock pulse.
Master-Slave JK Flip-Flop
• Fig. 2.4.27 shows the master-slave JK
flip-flop. Positive clock pulses are applied to first flip-flop and inverted
(negative) clock pulses are applied to second flip-flop. (See Fig. 2.4.27 on
next page)
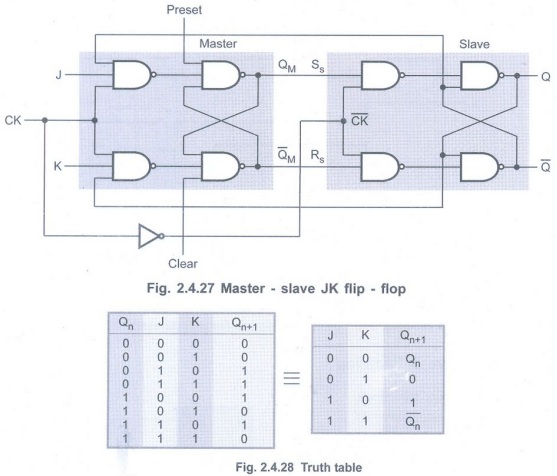
• When CK = 1, the first flip-flop is
enabled and the outputs QM and ![]() responds to the inputs of
J and K according to the Fig. 2.4.28. At this time, the second flip-flop is
inhibited because its clock is low,
responds to the inputs of
J and K according to the Fig. 2.4.28. At this time, the second flip-flop is
inhibited because its clock is low, ![]() .
.
• When CK goes Low (![]() ), the
first flip-flop is inhibited and second flip-flop is enabled. At this time, the
output of second flip-flop (Q and
), the
first flip-flop is inhibited and second flip-flop is enabled. At this time, the
output of second flip-flop (Q and ![]() ) follow the outputs QM and
) follow the outputs QM and ![]() ,
respectively.
,
respectively.
• Since the second flip-flop follows the
first one, it is referred to as the slave and the first one as the master.
• In master-slave JK flip-flop state
change occurs when flip-flop goes through both positive transition (first half)
of clock and negative transition of the clock (second half). Thus, race-around
condition does not exist in the master-slave JK flip-flop.
T Flip-Flop
• T flip-flop is also known as 'Toggle
flip-flop'.
• The T flip-flop is a modification of
the JK flip-flop.
• As shown in the Fig. 2.4.29, the T
flip-flop is obtained from a JK flip-flop by connecting both inputs, J and K
together.
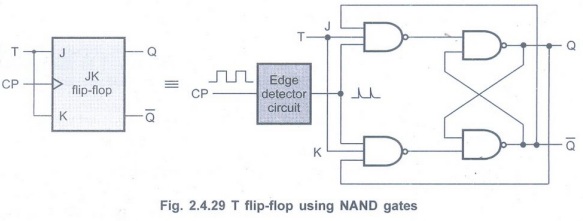
• When T = 0, J = K = 0 and hence there
is no change in the output. When T = 1, J = K = 1 and hence output toggles.
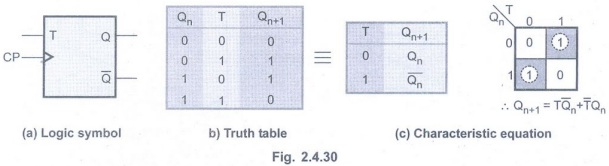
• The Fig. 2.4.30 shows logic symbol,
truth table and the characteristic equation for T flip-flop.
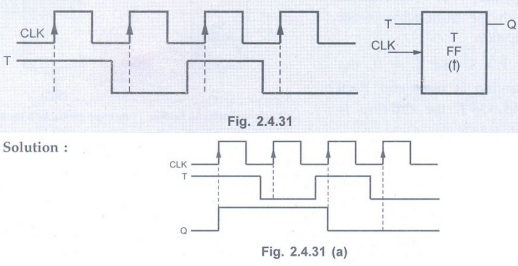
Example 2.4.5
Refer Fig. 2.4.31 and determine the Q output waveform if the flip-flop
starts out RESET.
Asynchronous or Direct Inputs
•For the flip-flops discussed so far,
the SR, D, JK and T, the inputs are called synchronous inputs because data on
these inputs are transferred to the flip-flop's output only on the triggering
edge of the clock pulse; that is, the data are transferred synchronously with
the clock.
• When power is turn ON, the state of
the flip-flop is uncertain. It may come to set (Q= 1) or reset (Q= 0) state.
• In many applications, it is necessary
to initially set or reset the flip-flop. Such initial state of flip-flop can be
accomplished by using the direct or asynchronous inputs of the flip-flop. These
inputs are: ![]() and
and ![]() . They can be applied at any time between clock pulses
and are not in synchronism with the clock.
. They can be applied at any time between clock pulses
and are not in synchronism with the clock.
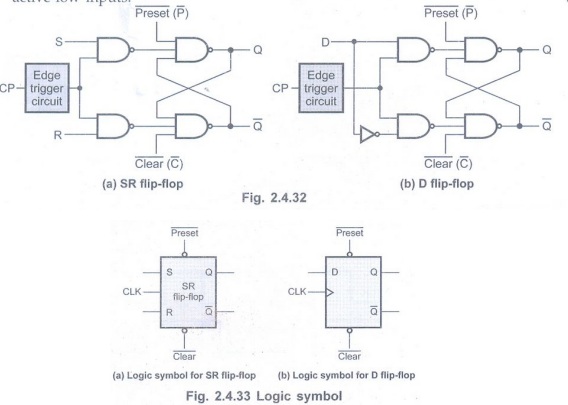
SR and D Flip-Flops with Preset and
Clear Inputs
• Fig. 2.4.32 shows the SR and D
flip-flops with preset and clear inputs. These are active-low inputs.
• When ![]() =
= ![]() = 1, the circuit operates
in accordance with the truth table of SR flip-flop.
= 1, the circuit operates
in accordance with the truth table of SR flip-flop.
• If ![]() = 1, and
= 1, and ![]() = 0, the flip-flop is
reset and
= 0, the flip-flop is
reset and ![]() = 0, and
= 0, and ![]() = 1,the flip-flop is set.
= 1,the flip-flop is set.
Note Condition ![]() =
= ![]() = 0 must not be used, since this leads to an uncertain state.
= 0 must not be used, since this leads to an uncertain state.
JK Flip-Flop with Preset and Clear
Inputs
• The JK flip-flop with preset and clear
is shown in Fig. 2.4.34.

• If preset and clear inputs are 1, the
circuit operates in accordance with the truth table of JK flip-flop given in
Fig. 2.4.18 (c).
• If preset = 0 and clear = 1, the
output of NAND gate 1 will certainly be 1. Consequently, all the three inputs
to NAND gate 2 will be 1 which will make ![]() = 0.
= 0.
• Making preset=0 sets the flip-flop.
• Preset signal is active when it is low,
hence it is active low signal.
• Low (0) on the clear input resets the
flip-flop making ![]() = 1.
= 1.
Assume J = K = 1
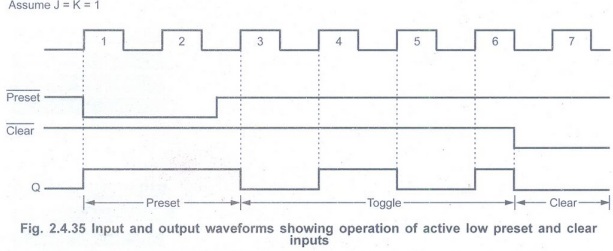
• A logic symbol for a JK flip-flop with
active low preset and clear inputs is shown in the Fig. 2.4.34 (a). These
inputs are active low, therefore they must both be kept high for synchronous
operation.
• The Fig. 2.4.35 illustrates the operation of active low preset and clear inputs.
• During clock pulse 1 and 2
the ![]() is low, keeping the flip-flop set regardless of the
synchronous inputs.
is low, keeping the flip-flop set regardless of the
synchronous inputs.
• For clock pulses 3, 4, 5 and 6, toggle
operation occurs because J and K both are high with preset and clear inactive.
• For clock pulse 7, the ![]() input
is low, keeping the flip-flop reset regardless of the synchronous inputs.
input
is low, keeping the flip-flop reset regardless of the synchronous inputs.
• In some IC packages preset and clear
inputs are active high. In those cases preset and clear input must both be kept
low for synchronous operation.
Review Questions
1. Explain the working of a master-slave JK flip-flop. AU May-03, 05, 08, 19, Dec.-03, 06, 08, 09, Marks 6
2. With reference to a JK flip-flop, what is racing? AU May-04, Dec.-08, 14, Marks 2
3. Draw the circuit for SR flip-flop. AU
May-05, 10, Marks 2
4. What is race around condition and how
is it overcome? Explain these concepts with relevant timing diagrams. AU
May-06, 08, Dec.-10, 14, Marks 8
5. Draw the clocked RS flip-flop and explain with truth table. AU May-07, Marks 2
6. How does a JK flip-flop differ from the SR flip-flop in its basic operation? AU May-07, Marks 2
7. Draw the logic symbol and truth table
of a D flip-flop. AU May-08, Marks 2
8. Draw the logic circuit of a clocked
JK flip-flop. AU May-08, Marks 2
9. Draw the logic diagram of a D-FF using NAND gates and explain. AU: Dec.-08, Marks 6
10. Mention any two differences between the edge triggering and level triggering. AU May-10, Marks 2
11. Write down the characteristic equation and truth table for the JK flip-flop. AU May-10, Marks 4
12. Mention the major application of
master slave flip-flop. AU Dec.-10, Marks 2
13. Give the block diagram of
maser-slave D flip-flop. AU May-15, Marks 2
14. Draw the diagram of T flip flop and
discuss its working. AU Dec.-15, Marks 2
15. Explain the use of asynchronous
inputs.
16. Draw and explain the working of
clocked D flip-flop.
17. Explain the operation of
master-slave SR flip-flop.
18. How the race condition can be
avoided in a flip flop? AU: Dec.-16, Marks 8
19. Design and implementation of SR flip-flop using NOR gate. AU: Dec.-18, Marks13
20. Describe the operation of R-S flip
flop a neat sketch. AU May-19, Marks 5
Digital Principles and Computer Organization: Unit II (a): Synchronous Sequential Logic : Tag: : Synchronous Sequential Logic - Digital Principles and Computer Organization - Flip-Flops
Related Topics
Related Subjects
Digital Principles and Computer Organization
CS3351 3rd Semester CSE Dept | 2021 Regulation | 3rd Semester CSE Dept 2021 Regulation
