Five - Variable K-Map

Five-Variable K-Map

A 5-variable K-map requires 2⁵ =32 cells, but adjacent cells are difficult to identify on a single 32-cell map. Therefore, two 16-cell K-maps are generally used. If the variables are A, B, C, D and E two identical 16-cell maps containing B, C, D and E can be constructed. One map is then used for A and the other for Ā. 

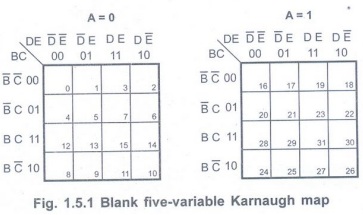
See Fig. 1.5.1. It is important to note that in order to identify the adjacent groupingin the five variable map, we must imagine the two maps superimposed on one another; not "hinged" or "mirror imaged". Every cell in one map is adjacent to the corresponding cell in the other map, because only one variable (i.e. A) changes between such corresponding cells. Thus, every row on one map is adjacent to the corresponding row (the one occupying the same position) on the other map, as are corresponding columns. Also, the rightmost and leftmost columns within each 16-cell map are adjacent, just as they are in any 16-cell map, as are the top and bottom rows. However, the rightmost column of one map is not adjacent to the leftmost column of the other map, since those are not corresponding columns. Nor is the top row of one map adjacent to the bottom row of the other. This is illustrated in Fig.

Examples for Understanding

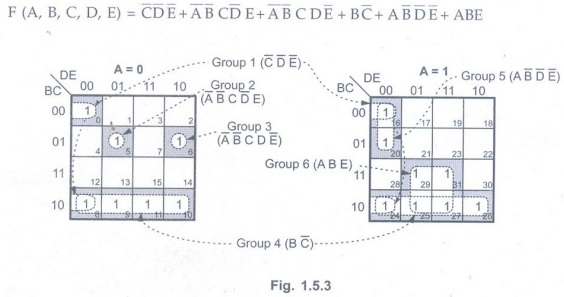
Example 1.5.1 Simplify the Boolean function.

F(A, B, C, D, E) = Σm (0, 5, 6, 8, 9, 10, 11, 16, 20, 24, 25, 26, 27, 29, 31)

Solution: As shown in the Fig. 1.5.3 there are two isolated 1s. These 1s are referred as group 2 and group 3, respectively. Group 1 is formed by combining two adjacent pair of 1s from two different 16-cell maps. The combination of two quads from two different 16-cell maps gives the group 4. The second 16-cell map has one pair and another quad which form group 5 and group 6 respectively. Therefore the simplified expression is

Example 1.5.2 Reduce the function using K-map technique

F(A, B, C, D, E) = ∑m (1, 4, 8, 10, 11, 20, 22, 24, 25, 26) + d (0, 12, 16, 17) 

Solution: The given function is plotted on the K-map with don't care conditions as shown in the Fig. 1.5.4. Here don't care conditions are taken as 1s to form pairs and quads. The group 1 is formed by combination of two pairs from two different 16-cell maps. Group 2 is quad within the first 16-cell map group 3 is formed by another combination of two pairs from two different 16-cell maps. The first 16-cell has one more pair of 1s which is referred to as group 4. Group 5 and group 6 are the quad and pair from the second 16-cell map, respectively.

Example 1.5.3 Simplify the following switching function

f(x₁, x₂, x₃, x₄, x₅) = ∑m (1,3,6,10,11,12, 14, 15, 17, 19, 20, 22, 24, 29, 30)

 AU May-08, Marks 8

Solution :

Examples for Practice