Finite Automata with Epsilon Transitions

Finite Automata with Epsilon Transitions

• The ɛ-transitions in NFA are given in order to move from one state to another without having any symbol from input set Σ.

Consider the NFA with ɛ as:

• In this NFA with ε, q₀ is a start state with input 0 one can be either in state qo or in state q₁. If we get at the start a symbol 1 then with ε - move we can change state from q₀ to q₁ and then with input we can be in state q₁.

• On the other hand, from start state q₀, with input 1 we can reach to state q₂.

• Thus it is not definite that on input 1 whether we will be in state q₁ or q₂. Hence it is called nondeterministic finite automata (NFA) and since there are some ε moves by which we can simply change the states from one state to other. Hence it is called NFA with ε.

Definition of NFA with ε

The language L accepted by NFA with &, denoted by M = (Q, Σ, δ, q₀, F) can be defined as:

Let, M = (Q, Σ, δ, q₀, F) be a NFA with ε.

Where

Q is a finite set of states.

Σ is input set.

δ is a transition or a mapping function for transitions from Q×{ΣUε} to 2^Q.

q₀ is a start state.

F is a set of final states such that F ϵ Q.

Example 1.8.1 Construct NFA with ε which accepts a language consisting the strings of any number of a's followed by any number of b's. Followed by any number of c's.

Solution: Here any number of a's or b's or c's means zero or more in number. That means there can be zero or more a's followed by zero or more b's followed by zero or more c's. Hence NFA with ε can be -

Normally ε's are not shown in the input string. The transition table can be -

We can parse the string aabbcc as follows -

δ (q₀, aabbcc) Ⱶ δ (q₀, abbcc)

Ⱶ δ (q₀, bbcc)

Ⱶ δ (q₀, εbbcc)

Ⱶ δ (q₁, bbcc)

Ⱶ δ (q₁, bcc)

Ⱶ δ (q₁, cc)

Ⱶ δ (q₁, εcc)

Ⱶ δ (q₂, cc)

Ⱶ δ (q₂, c)

Ⱶ δ (q₂, ε)

Thus we reach to accept state, after scanning the complete input string.

Definition of ε - closure

The ε - closure (p) is a set of all states which are reachable from state p on ε - transitions such that:

i) ε - closure (p) = p where p ϵ Q.

ii) If there exists ε closure (p) = {q} and δ(q,ε) = r then

ε - closure (p) = {q, r}

Example 1.8.2 Find ε - closure for the following NFA with ε.

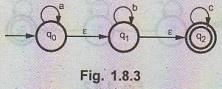
Solution:

ε - closure (q₀) = {q₀, q₁, q₂} means self state + ε - reachable states.

ε - closure (q₁) = {q₁, q₂} means q₁ is a self state and q₂ is a state obtained from q₁ with ε input.

ε - closure (q₂) = {q₂}

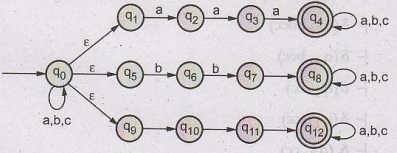
Example 1.8.3 Build a non-deterministic FSM with & that accepts

L = {w = {a, b, c)*: w contains at least one string that consists of three identical symbolds in a row). For example

• The following strings are in L are aabbb, baabbbccc

• The following strings are not in L are ε, aba, abababab, abcbcab.

Solution: The NDFSM with ε is