Finite Automata (FA)

Finite Automata (FA)

Definition

A finite automata is a collection of 5-tuple (Q, Σ, δ, q₀, F) where,

Q is a finite set of states, which is non empty.

Σ is input alphabet, indicates input set.

Q₀ is an initial state and q₀ is in Q i.e. q₀ ϵ Q.

F is a set of final states.

δ is a transition function or a mapping function. Using this function the next state can be determined.

Finite Automata Model

• The finite automata can be represented using

i) Input tape - It is a linear tape having some number of cells. Each input symbol is placed in each cell.

ii) Finite control - The finite control decides the next state on receiving particular input from input tape. The tape reader reads the cells one by one from left to right and at a time only one input symbol is read. (Refer Fig. 1.5.1)

• For example: suppose current state is q, and suppose reader is reading the symbol 'a' then it is finite control which decides what will be the next state at input 'a'. The transition from current state q with input w to next state q' producing w' will be represented as,

(q, w) Ⱶ (q', w')

If w is a string and M is a finite automata, then w is accepted by the FA

iff        (w, s) Ⱶ (q, ε)

with q as final state.

• The set of strings accepted by a FA given by M then M is accepted by language L. The acceptance of M by some language L is denoted by L (M).

• A machine M accepts a language L iff, 

L = L (M).

Representation of Finite Automata

The strings and languages can be accepted by a finite automata, when it reaches to a final state. There are two preferred notations for describing automata :

1. Transition diagram

A transition diagram or transition graph can be defined as collection of –

1) Finite set of states K.

2) Finite set of symbols Σ.

3) A non empty set S of K. It is called start state.

4) A set F  K of final states.

5) A transition function K×A →K with K as state and A as input from Σ*

The notations used in transition diagram are -

For example:

The FA can be represented using transition graph. The machine initially is in start state S₀ then on receiving input 0 it changes to state S₁. From S₀ receiving input 1 the machine changes its state to S₄. The state S₂ is a final state or accept state. When we trace the input for transition diagram and reach to a final state at end of input string then it is said that the given input is accepted by transition diagram.

Another example:

We have drawn a transition diagram for the input aabb.

Note that the start state is S₀ and final state is S₄. The input set is Σ = {a,b}. The states S₁, S₂, S₃ are all intermediate states.

2. Transition table

This is a tabular representation of finite automata. For transition table the transition function is used.

For example:

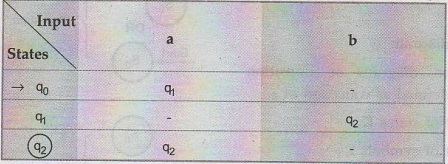
The rows of the table corresponds to states and columns of the table correspond to inputs. Here q₀ is start state, q₂ is final state.

Types of Automata

There are two types of finite automata -

i) Deterministic Finite Automata.