Example Problems of Uninformed Search Strategies

UNIT I

Chapter: 3: Uninformed Search Strategies

Example Problems

AU Dec.-10, 14, May-14

There are variety of task environments ranging from easier to complex ones, therefore problem solving approach should be realistic which can give solution for any type of task environment which in turn is useful for mankind. Problems can be categorized as toy problems and real-world problems.

Toy Problem

A Toy problem is a problem which illustrates various problem-solving methods.

Characteristics of Toy problem

1) For the Toy problem exact and precised description can be given.

2) These problem provide basis for solving some real-life problems.

3) They can be used by researchers to compare performance of algorithms.

For example: 8-queen puzzle, vacuum world, ball picker robot.

Real World Problem

A real-world problem is a problem which needs to be solved so that its solution can be utilized in practical life. They will not have some predefined. Well described, single specification. In fact while considering these problem general formulation needs to be done.

People do care about the solutions of real-world problem as they are benefited from it.

For example: Route finding for a trip, Travelling salesman problem, Robot navigation, Car reversing guide.

Problem Formulation for Toy Problems

Now let us see some toy problem examples.

Each example gives all 4 aspects of problem formulation namely

1) Initial state

2) Successor function

3) Goal state

4) Path cost.

Also we list all the possible states of problem solution, through which agent can pass or move.

Example 1 Ball Picker Robot Problem Formulation

Problem statement: 2 buckets are full of balls. Either a ball is white colour or red colour. Objective is to pick all black colour balls from bucket.

1) Initial state: Any state can be designated as initial state.

2) Successor function:

This function generates legal states that result from trying the three actions (Left, Right, Pick Black colour ball).

3) Goal test:

This checks if all Black coloured balls from both the buckets are picked up.

4) Path cost: Each step cost is 1, so path cost is the number of steps in the path.

5) States:

The agent is at one of the 2 location (at bucket A or at bucket B), from each of which black colour balls may have been picked up completely or may not be.

Thus there are 2 (locations) x 2^{2(Two possiblities)} = 8 possible world states.

• Comparison with real world -

If we compare with real world situation we can see that above toy problem has all well specified description. Agent has discrete location (in real world many locations can be there, also as time passes over, more locations can come up). Agent has discrete pick up item i.e. Black colour ball (In real world this items can have more dimensions). Also once all Black colour balls are picked up from bucket then again new black colour balls are not expected. (Where as in real world we may expect bucket to have new Black colour balls).

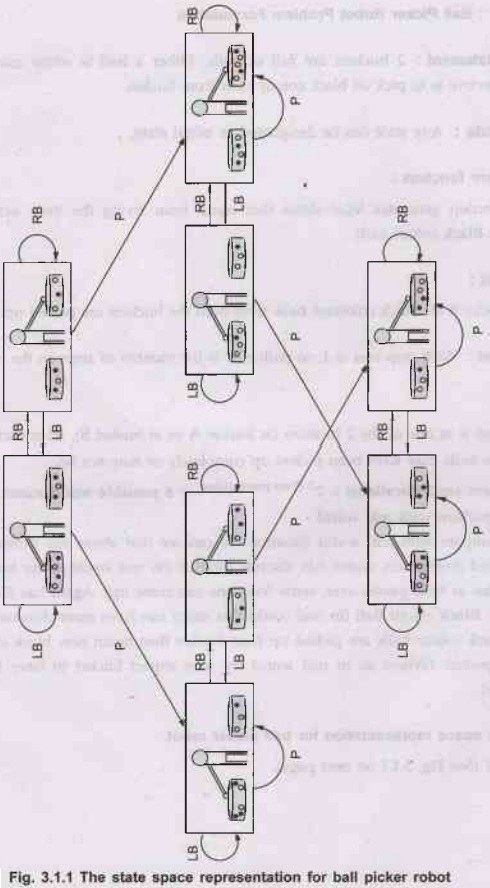
• The state space representation for ball picker robot

Fig. 3.1.1 (See Fig. 3.1.1 on next page).

Example 2: 8-Queen Problem

Problem Statement: Given a chess board of 8x8 size, objective is to place 8 queens on a chess board such that no two queens are attacking. (A queen same row, column or diagonal).

1) Initial state: No queens on the board.

2) Successor function:

Add a queen to any empty square, such that it do not attack other queen.

3) Goal test: 8-queens on the board such that no queens attack each other.

4) Path cost: Each step costs 1, so the path cost is the number of steps in the path.

5) States: Any arrangements of 1 to 8 queens on the board is a state. This formulation has, 64 x 63 x...57≈ 3×10¹⁴ possible sequences to investigate. But the condition of non-attacking reduces the states to 2057 from 3×10¹⁴.

Example 3: 8-Puzzle

Problem Statement: Consists of 3x3 board with eight numbered tiles and a blank space. A tile adjacent to the blank space can slide into the space. The object is to reach a specified goal state, such as the one shown on the right of the figure.

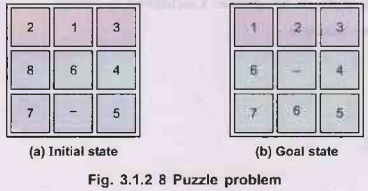
1) States:

A state description specifies the location of each of the eight tiles and the blank in one of the nine squares.

2) Initial state:

Any state can be designated as the initial state. Note that any given goal reached from exactly half of the possible initial states.

3) Successor function:

This function generates the legal states that result from trying the four actions. (blank moves, left, right, up or down).

Example 4 -Cryptarithmetic

Problem Statement: Find an assignment of digits (0, ..., 9) to letters so that a given arithmetic expression is true.

For example - Applying digit to a letter.

1) States: Puzzle with letters and digits.

2) Initial state: Only letters present.

3) Successor function (operators): Replace all occurrences of a letter by a digit not used yet.

4) Goal test: Only digits in the puzzle. Calculation is correct.

Solution for above example -

F = 2, O = 9,

R = 7, T = 8,

Y = 6, E = 5,

N = 0,I = 1,

X = 4, S = 3.

5) Goal test: This checks whether the state matches the goal configuration.

6) Path cost: Each step costs 1, so the path cost is the number of steps in the path.

Example 5 - Missionaries and Cannibals

• Problem Statement:   

There are 3 missionaries, 3 cannibals, and 1 boat that can carry upto two people on one side of a river.

Goal: Move all missionaries and cannibals across the river.

Constraint: Missionaries can never be out numbered by cannibals or either side ofthe river, or else the missionaries are killed.

1) States

• Number of missionaries, cannibals, and boats on the banks of a river

• Illegal states: Missionaries are outnumbered by cannibals on either bank.

2) Initial states

• All missionaries, cannibals and boats are on one bank.

3) Successor function (operators)

• Transport a set of upto two participants to the other bank

{1 missionary} or {1 cannibal } or {2 missionaries } or {2 cannibals } or

{1 missionary and 1 cannibal }

4) Goal test

• Nobody left on the initial river bank.

5) Path cost

• Number of crossings.

• Also known as "Goats and cabbage, Wolves and sheep", etc.

Example 6 - Water Jug Problem

Problem Statement: Given 3 jugs (9, 5 and 3 liters), a water pump and a sink, how do you get exactly 7 liters into the 9 litre jug.

1) State:

(X, Y, Z) for liters in jugs 1, 2 and 3. Integers 0 to 9 are assigned to all possible permutations of 1, 2, 3.

Operations -

Empty jug, fill jug

Ex = fill (0, 5, 0)

2) Initial state: (0, 0, 0)

3) Goal state: (X, X, 7)

4) Solution sequence: (5, 0, 0 (0, 5, 0 (0, 0, 0 etc)

Real-World Problem Examples

Example 1 - General Route Finding Problem

Problem Statement: Route-finding problem is defined in terms of specified locations and transitions along links between them. Route-finding algorithms are used in a variety of applications, such as routing in computer networks, military operations planning, and air line travel planning systems.

1) States: Locations

2) Initial state: Starting point

3) Successor function (operators): Move from one location to another.

4) Goal test: Arrive at a certain location.

5) Path cost: May be quite complex, which can involve factors like, Money, time, travel, comfort, scenery, ... etc.

• Simplified Example of Route Finding Problem [Airline Travelling Problem]

Problem Statement: Starting from initial location one has to reach at the specified destination by some prespecified time.

1) States: Each state is represented by a location (e.g. an airport) and the current time.

2) Initial state: This is specified by the problem.

3) Successor function:

This returns the states resulting from taking any scheduled flight (perhaps further specified by seat class and location), leaving later than the current time plus the time within-airport transit time, from the current airport to another.

4) Goal test: Are we at the destination by some prespecified time?

5) Path cost:

This depends on monetary cost, waiting time, flight time, customs and immignation procedures, seat quality, time of day, type of airplane, frequent-flyer mileage awards, and so on.

Example 2 - Travelling Sales Person Problem

Problem Statement: It is a touring problem in which each city must be visited exactly once. The aim is to find the shortest tour. The problem is known to be NP-hard.

1) States

• Locations/cities.

• Illegal states.

   a) Each city may be visited only once.

   b) Visited cities must be kept as state information.

2) Initial state

• Starting point.

• No cities visited.

3) Successor function (operators)

• Move from one location to another one.

4) Goal test

• All locations visited.

• Agent at the initial location.

5) Path cost

• Distance between locations.

In addition to planning trips for traveling sales persons, these algorithms have been used for tasks such as planning movements of automatic circuit-board drills, and for stocking machines on shop floors.

Example 3 - VLSI Layout Problem

Problem Statement: A VLSI layout problem requires positioning millions of components and connections on a chip to minimize area, minimize circuit delays, minimize stray capacitances, and maximize manufacturing yield.

1) States

• Positions of components, wires on a chip.

2) Initial state

• Incremental: No component placed.

• Complete-state: All components place (e.g. randomly, manually).

3) Successor function (operators)

• Incremental: Place components, route wire.

• Complete-state: Move component, move wire.

4) Goal test

• All components placed.

• Components connected as specified.

5) Path cost

• May be complex.

One can consider distance, capacity, number of connections per component, for path cost computation.

Detail description of VLSI layout problem

When logical design is made, the layout problem come and the problem is divided into two parts 1) Cell layout 2) Channel routing as below -

1) Cell layout

a) The basic components of circuit are grouped into cells, each cells perform some recognition. The cells of standard size are connected to each of the other cell.

b) The overlapping between the cell component is avoided. Some sort of room is provided for connecting wires.

2) Channel routing

a) The cell components are fixed on a chip.

b) The channel routing task is to search a particular route for each wire. The functional task is achieved through the gaps between the cells.

c) The complex algorithm are designed to perform the channel routing. The degree of complexity is so high, but it is always possible to solve problem with specific algorithm.

Example 4 - Robot Navigation

Problem Statement: Robot navigation is a generalization of the route-finding problem. Rather than a discrete set of routers, a robot can move in a continuous space with (in principle) an infinite set of possible actions and states. For a circular robot moving on a flat surface the space is essentially two-dimensional. When the robot has arms and legs or wheels then it must also be controlled, the search space becomes many-dimensional.

1) States

• Locations.

• Position of actuators.

2) Initial state

• Start position (dependent on the task).

3) Successor function (operators)

• Movement, actions of actuators.

4) Goal test

• Task-dependent.

5) Path cost

• May be very complex.

• Distance, energy consumption.

Example 5 - Assembly Sequencing

Problem Statement: In assembly problems, the aim is to find an order in which to assemble the parts of some object. If the wrong order is chosen, there will be no way to add some part later in the sequence without undoing some of the work already done. Checking a step in the sequence for feasibility, is a difficult geometrical search problem, closely related to robot navigation.

1) States

• Location of components.

2) Initial state

• No components assembled.

3) Successor function (operators)

• Place component.

4) Goal test

• System fully assembled.

5) Path cost

Number of moves

Another example of assembly sequencing is protein design, in which the goal is to find a sequence of amino acids that with fold into a three-dimensional protein with the right properties to cure some disease.