Euler and Hamilton Paths

Euler and Hamilton paths

Definition: Euler circuit

An Euler circuit in a graph G is a simple circuit containing every edge of G.

Definition: Euler path

An Euler path in G is a simple path containing every degree of G.

Example 1. Which of the graphs in Figures has an Euler circuit? Of those that do not, which have an Euler path?

Solution: G₁ has an Euler circuit, for example, a, e, c, d, e, b, a.

Neither G₂ or G₃ has an Euler circuit.

However, G₃ has an Euler path, namely, a, c, d, e, b, d, a, b. G₂ does not have an Euler path.

The graph H₂ has an Euler circuit, for example, a, g, c, b, g, e, d, f, a.

Neither H₁ nor H₃ has an Euler circuit.

H₃ has an Euler path, namely, c, a, b, c, d, b, but H₁ does not.

Definition: Eulerian trail

A trail in G is called an Eulerian trail if it includes each edge of G exactly once.

Definition: Euler line, Euler graph

A closed walk which contains all edges of the graph G is called an Euler line, and the graph containing atleast one Euler line is said to be an Euler graph.

Note: Euler line is also some times called Euler circuit.

Example 2. Give two examples of Euler graph.

Solution :

Theorem: A given connected graph G is an Euler graph iff all vertices of G is of even degree.

Proof: Suppose, G is an Euler graph.

→ G contains an Euler line

→ G contains a closed walk covering all edges.

To prove :

All vertices of G is of even degree.

In training the closed walk, every time the walk meets a vertex v, it goes through two new edges incident on V with one we 'entered' and other 'exited'. This is true, for all vertices, because it is a closed walk. Thus the degree of every vertex is even.

Conversely, suppose that all vertices of G are of even degree.

To prove :

G is an Euler graph.

(i.e.,) to prove G contains an Euler line.

Construct a closed walk starting at an arbitrary vertex v and going through the edge of G such that no edge is repeated. Because, each vertex is of even degree, we can exit from each end, every vertex where we enter, the tracing can stop only at the vertex v. Name the closed walk as h.

Case (i)

If h covers all edges of G, then h becomes an Euler line, and hence, G is an Euler graph.

Case (ii)

If h does not cover all edges of G then remove all edges of h from g and obtain the remaining graph G'. Because both G and G' have all their vertex of even degree.

→ Every vertex in G' is also of even degree.

Since G is connected, h will touch G' atleast one vertex v'. Starting from v', we can again construct a new walk h' in G'. This will terminate only at v', because, every vertex in G' is also of even degree.

Now, this walk h' combined with h forms a closed walk starts and ends at v and has more edges than h. This process is repeated until we obtain a closed walk covering all edges of G. Thus G is an Euler graph.

Theorem: A connected multigraph with at least two vertices has an Euler circuit if and only if each of its vertices has even degree.

Theorem: A connected multigraph has an Euler path but not an Euler circuit if and only if it has exactly two vertices of odd degree.

Proof: First Part :

Given: A connected multigraph G has an Euler path but not an Euler circuit.

To prove: G has exactly two vertices of odd degree suppose that a connected multigraph does have an Euler path from a to b, but not an Euler circuit. The first edge of the path contributes one to the degree of a. A contribution of two to the degree of a is made every time the path passes through a. The last edge in the path contributes one to the degree of b.

Every time the path goes through b there is a contribution of two to its degree. Consequently, both a and b have odd degree. Every other vertex has even degree, because the path contributes two to the degree of a vertex whenever it passes through it.

Second Part :

Given The graph has exactly two vertices of odd degree.

To prove: G has an Euler path

Suppose that a graph has exactly two vertices of odd degree, say a and b. Consider the larger graph made up of the original graph with the addition of an edge {a, b}.

Every vertex of this larger graph has even degree, so there is an Euler circuit. The removal of the new edge produces an Euler path in the original graph.

Chinese postman problem :

If a postman can find an Euler path in the graph that represents. the streets the postman needs to cover, this path produces a route that traverses each street of the route exactly once. If no Euler path exists, some streets will have to be traversed more than once. This problem is known as the Chinese postman problem.

Theorem

Show that a directed multigraph having no isolated vertices have an Euler path but not an Euler circuit if and only if the graph is weakly connected and the in-degree and out degree of each vertex are equal for all but two vertices, one that has in-degree one larger than its out-degree and the other that has out-degree one larger than its in-degree.

Proof: If there is an Euler path, as we follow it each vertex except the starting and ending vertices must have equal in-degree and out-degree, since whenever we come to a vertex along an edge, we leave it along another edge. The starting vertex must have out-degree 1 larger than its in-degree, since we use one edge leading out of this vertex and whenever we visit it again we use one edge leading into it and one leaving it.

Similarly, the ending vertex must have in-degree 1 greater than its out-degree. Since the Euler path with directions erased produces a path between any two vertices, in the underlying undirected graph, the graph is weakly connected.

Conversely, suppose the graph meets the degree conditions stated. If we add one more edge from the vertex of deficient out-degree to the vertex X with equal in-degree and out-degree. Because the graph is still weakly connected, by this new graph has an Euler circuit. Now delete the added edge to obtain the Euler path.

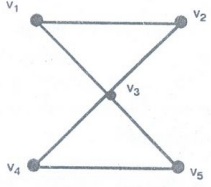
Example 3. Let G be a graph, verify that G has an Eulerian circuit,

Solution: Here G is connected and all the vertices are having even degree deg (v₁) = deg (v₂) = deg (v₄) = deg (v₅) = 2

Thus G has a Eulerian circuit, we find the Eulerian circuit.

v₁ - v₃ - v₅ - v₄ - v₃ - v₂ - v₁

Example 4. Show that the graph, has no Eulerian circuit but has a Eulerian trail.

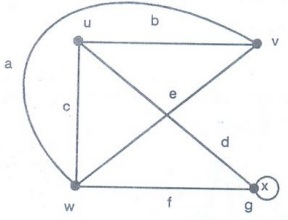
Solution: Here deg (u) = deg (v) =3 and deg (w) = dég (x) = 4, because u and v have only two vertices of odd degree, the graph does not contain Eulerian circuit, but the path b – a – c – d – g – f – e is an Eulerian trail.

Example 5. Show that the graphs contain no Eulerian circuit.

Solution: The graph does not contain Eulerian circuit since it is not connected.

Example 6. Which of the following graphs are Eulerian ?

(i) the complete graph K₅

(ii) the complete bipartite graph K_2,3

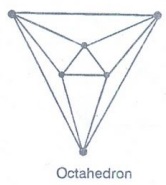
(iii) the graph of the octahedron

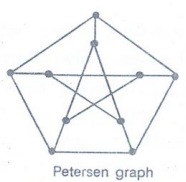
(iv) the Petersen graph

Solution :

(i) We know that the degree of each vertex in the comple graph K₅ is 5 - 1 = 4 which is even.

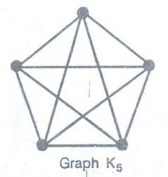
Hence degree of each vertex in K₅ is even.

Because Ks is also a connected graph, therefore by theorem K₅ is an Euler graph.

(ii) The graph K_2,3 is given below :

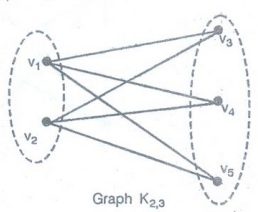
It is clear that each vertex in the graph K_2,3 is not of even degree. Hence the graph K_2,3 is not Euler.

(iii) We know from figure that each vertex in the graph of the octahedron is of degree 4 which is even.

Hence the graph of the octahedron is an Euler graph.

(iv) From figure, it is clear that the Petersen graph is not an Euler graph since each vertex of this graph is of degree 3 which is not even.

Example 7. Fow that values of n is the graph K_n Eulerian?

Solution: We know that K_n, the complete graph of n vertices is a connected graph in which degree of each vertices is n-1. Because a graph is Eulerian if and only if it is connected and degree of each vertex is even, we conclude that K_n is an Euler graph if and only if n is odd.

Example 8. Which complete bipartite graphs K_m,n are Euler graphs?

Solution: From the definition of K_m,n graph that it is an Euler graph if and only if both m and n are even.

Example 9. The graph shown in figure is an Euler graph. Determine Euler circuit for this graph.

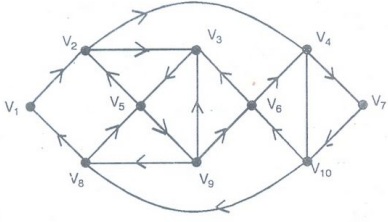
Solution: The Euler circuit for this graph is

V₁, V₂, V₃, V₅, V₂, V₄, V₇, V₁₀, V₆, V₃, V₉, V₆, V₄, V₁₀, V₈, V₅, V₉, V₈, V₁

Example 10. Explain Konisberg bridge problem. Represent the problem by means of graph. Does the problem have a solution?

Solution: There are two islands A and B formed by a river. They are connected to each other and to the river banks C and D by means of 7 bridges. The problem is to start from any one of the 4 land areas A, B, C, D, walk across each bridge exactly once and return to the starting point.

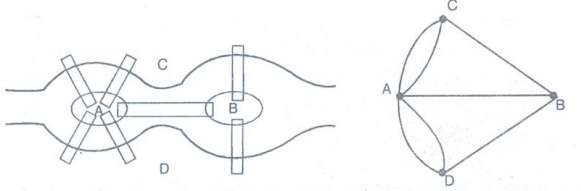
This problem is the famous Konisberg bridge problem.

When the situation is represented by a graph, with vertices representing the land areas and the edges and the bridges.

This problem is the same as that drawing the graph without lifting the pen from the paper and without retracing any line.

In other words, the problem is to find whether there is Eulerian circuit in the graph. But a connected graph has an Eulerian circuit if and only if each of its vertices is of even degree.

In the present case all the vertices are of odd degree. Hence, Konisberg bridge problem has no solution.

Example 11. Use Fleury's algorithm to produce an Euler circuit for the graph given below.

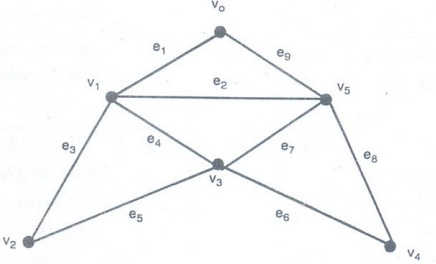
Solution: Degree of each vetex in the graph is of even degree, it has an Euler circuit, according to step 1 of Fleury's algorithm, we can begin from any vertex. Suppose we choose the vertex vo as the starting vertex. We summarize the results of applying steps 2 and 3 repeatedly in the following table :

Thus walk T₉, is an Euler circuit in this graph. Since at several places, there were more than one choices for the edges which could be deleted from the graph, therefore, there are many other Euler circuits in this graph.

Hamilton path and Hamilton circuits

Definition: Hamilton path

A simple path in a graph G that passes through every vertex exactly once is called a Hamilton path. That is, the simple path x₀, x₁, ..., x_n-1,x_n in the graph G = (V,E) is a Hamilton path if V = {x₀, x₁, …, x_n-1, x) and x_i = x_j for 0 ≤ i < j ≤ n

Definition: Hamilton circuit

A simple circuit in a graph G that passes through every vertex exactly once is called a Hamilton circuit. And the simple circuit x₀, x₁, …, x_n-1, x_n, x₀ (with n > 0) is a Hamilton circuit if x₀, x₁, …, x_n-1, x_n, is a Hamilton path.

Example 1. Does the graph given below have a Hamilton path? If so, find such a path. If it does not, give an argument to show why no such path exists.

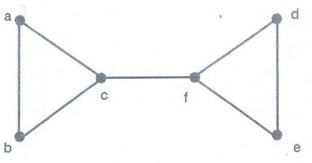
Solution: a, b, c, f, d, e is a Hamilton path.

Example 2. Does the graph given below have a Hamilton path? If so, find such a path. If it does not, give an argument to show why no such path exists.

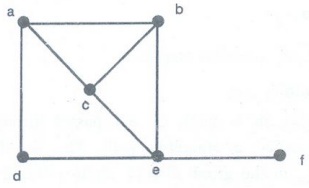
Solution: f, e, d, a, b, c is a Hamilton path.

Example 3. Does the graph given below have a Hamilton path? If so, find such a path. If it does not, give an argument to show why no such path exists.

No Hamilton path exists.

There are eight vertices of degree 2, and only two of them can be end vertices of a path.

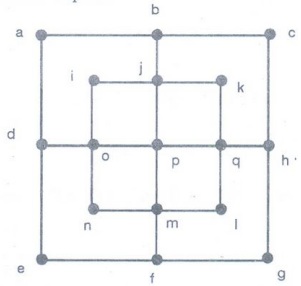
For each of the other six, their two incident edges must be in the path.

It is not hard to see that if there is to be a Hamilton path, exactly one of the inside corner vertices must be an end, and that this is impossible.

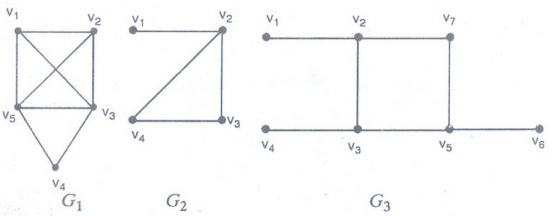
Example 4. Which of the simple graphs given below have a Hamilton circuit or, if not, a Hamilton path?

Solution :

(i) G₁ has a Hamilton circuit.

v₁, v₂, v₃, v₄, v₅, v₁

(ii) G₂ has no Hamilton circuit.

but G₂ has Hamilton path.

v₁, v₂, v₃, v₄

(iii) G₃ has neither a Hamilton circuit nor a Hamilton path. Since any path containing all vertices must contain one of the edges {a,b}, {e,f} and {c, d} morethan once.

Example 5. Show that K has a Hamilton circuit whenever n ≥ 3. [A.U N/D 2012]

Solution: Now we can form a Hamilton circuit in K_n beginning at any vertex.

Such a circuit can be built by visiting vertices in any order we choose, as long as the path begins and ends at the same vertex and visits each other vertex exactly once.

It is possible since there are edges in K_n between any two vertices.

Example 6. Show that the graph is Hamiltonian

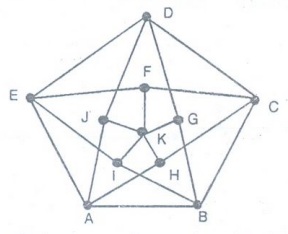
Solution: From figure we observe that the closed walk

A → H → C → F → E → D → G → B → I → K→ J→ A is a Hamiltonian circuit.

Hence the graph is Hamiltonian.

Example 8. Show that the following graph is not Hamiltonian.

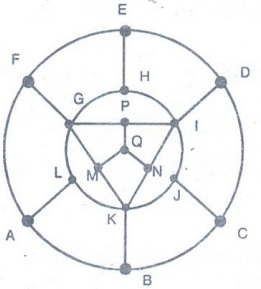
Solution: The given graph has 16 vertices and 27 edges. If the graph has a Hamiltonian circuit then this circuit will contain exactly 16 edges. We know that among all the edges incident on any vertex exactly two can be included in any Hamiltonian circuit.

In the above graph, we would have to eliminate one edge at A, three edges at K, three edges at G, one edge at E, three edges at I, one edge at C and one edge at Q.

Therefore at least 13 of the 27 edges of G cannot be included in any Hamiltonian circuit.

Thus we are left with 14 edges which cannot form a Hamiltonian circuit on the 16 vertices of G. Thus G has no Hamiltonian circuit.

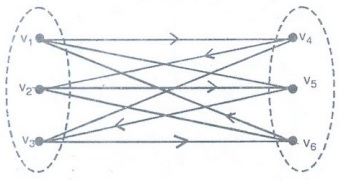
Example 27. Under what conditions on r and s does the complete bipartite graph K_{r, s} have a Hamiltonian circuit?

Solution: The vertex set of K_{r, s} can be decomposed into two disjoint subsets V₁ and V₂ containing r and s vertices respectively such that each edge in K_{r, s} joins a vertex in V₁ to a vertex in V₂. Because Hamiltonian circuit a closed walk that traverses every vertex of the graph exactly once, therefore Hamiltonian circuit in K_{r, s} exists only when r = s and both are ≥ 2

Example 9. Solve the travelling salesman problem for the graph in the following figure.

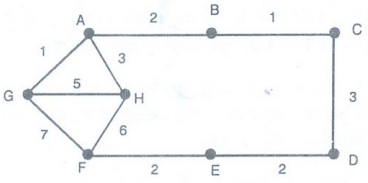
Solution :

This graph has the following two Hamiltonian circuits

(a) A → B → C → D → E → F → H → G → A

(b) A → B → C → D → E → F → G → H → A

The total weights of Hamiltonian circuits described in (a) and (b) are 22 and 25 respectively.

Because the total weight of Hamiltonian circuit in (a) is minimum, salesman should travel according to circuit in (a).

Example 10. Find a Hamiltonian path or a Hamiltonian circuit, if it exists in each of the three graphs given below. If it does not exist, explain why?

Solution: G₁ contains a Hamiltonian circuit, for example A-B-C-D-E-F-A. In fact there are 5 more Hamiltonian circuits in G₁, namely, A-B-C-F-E-D-A, A-B-E-D-C-F-A, A-B-E-F-C-D-A, A-D-C-B-E-F-A and A-D-E-B-C-F-A

G₂ contains neither a Hamiltonian path nor, a Hamiltonian circuit, since any path containing all the vertices must contain one of the edges A-B and E-F more than once.

Example 11. Give an example of a graph that has an Euler circuit and a Hamiltonian circuit, which are distinct.

Solution: The graph having an Euler circuit and a Hamiltonian circuit which are distinct is shown in figure.

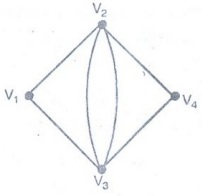
The Euler circuit is V₁, V₃, V₂, V₃, V₄, V₂, V₁

The Hamiltonian circuit is V₁, V₂, V₄, V₃, V₁

Example 12. Give an example of a graph which has a Hamiltonian circuit but not an Euler circuit.          [A.U M/J 2013]

Solution: The graph having a Hamiltonian circuit but not an Euler circuit is shown in figure.

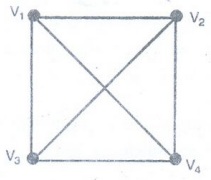
The Hamiltonian circuit is V₁, V₂, V₄, V₃, V₁.

There is no Euler circuit.

Example 13. Give an example of a graph which has an Euler circuit but not a Hamiltonian circuit.

Solution: The graph having an Euler circuit but not a Hamiltonian circuit is shown in figure.

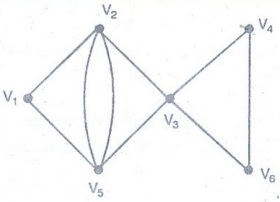
The Euler circuit is V1, V5, V2, V5, V3, V4, V6, V3, V2, V1.

There is no Hamiltonian circuit.

Example 14. In a complete graph with n vertices there are (n - 1)/2 edge-disjoint Hamiltonian circuits, if n is an odd number ≥ 3.

Proof: A complete graph G of n vertices has n (n - 1)/2 edges, and a Hamiltonian circuit in G consists of n edges.

Therefore, the number of edge-disjoint Hamiltonian circuits in G cannot exceed (n-1)/2. That there are (n - 1)/2 edge-disjoint Hamiltonian circuits, when n is odd.

The subgraph (of a complete graph of n vertices) in figure is a Hamiltonian circuit Keeping the vertices fixed on a circle, rotate the polygonal pattern clockwise by 360/(n - 1), 2,360/(n - 1), 3.360/(n - 1), ... , (n-3)/2.360 / (n-1) degrees. Observe that each rotation produces a Hamiltonian circuit that has no edge in common with any of the previous ones.

Thus we have (n - 3)/2 new Hamiltonian circuits, all edge disjoint from the one is figure and also edge disjoint among themselves. Hence the theorem.

Example 15. Show that a bipartite graph with an odd number of vertices does not have a Hamilton circuit.

Solution: Suppose that G = (V,E) is a bipartite graph with V = V₁ U V₂, wehre no edge connects a vertex in V₁ and a vertex in V₂.

Suppose that G has a Hamilton circuit. Such a circuit must be of the form a₁, b₁, a₂, b₂, a_k, b_k, …, a_k, b_k, a₁, where a_i ϵ V₁ and b_i ϵ V₂ for i = 1, 2, …, k. Since the Hamilton circuit visits each vertex exactly once, except for v1, where it begins and ends, the number of vertices in the graph equals 2k, an even number.

Hence, a bipartite graph with an odd number of vertices cannot have a Hamilton circuit.

Example 16. For which values of m and n does the complete bipartite graph K_{m, n} have a Hamilton circuit?

Solution: m = n ≥2

ORE'S THEOREM

If G is a simple graph with numb er of vertices n (≥3) and if

deg (u) + deg (v) ≥ n …..(1)

for every pair of non-adjacent vertices u and v, then G is Hamiltonian.

Proof: We shall prove the theorem by contradiction. We assume that there exists a non-Hamiltonian graph with n vertices satisfying the given condition (1) for every pair of non-adjacent vertices u and v. Among all such non-Hamiltonian graphs, let G be a non-Hamiltonian graph with maximum number of edges. Because G is maximal non-Hamiltonian, it follows that there exist two non-adjacent vertices u and v in G such that addition of an edge joining u and v will result in a Hamiltonian graph. in G, there is a Hamiltonian path.

u = u1, u2, u3, ...., u_n = v with u and v as the end vertices as shown in figure.

Define

S = {i: u_i is adjacent to vertex u in G}

T = {i: u_i is adjacent to vertex v in G}

Clearly, |S| = deg (u) and |T| = deg (v) in G where |X| denotes the number of elements in a set X. We assert that S∩T = ϕ and |SUT| ≤ n-1. For if, i ϵ S ∩ T, then the edges (u, u_i) and (u_i, v) would be in G and then u = u₁, u₂, …, u_i-1, u_i, u_n, u_n-1, ..., u_i+1, u₁ would form a Hamiltonian circuit in G, which is a contradiction. Further, SUT < {1, 2,.., n}. But since vertex u₁ = u is neither adjacent to u nor adjacent to v, 1ϵ SUT.

Therefore,

|SUT| ≤ n-1

Now, we have

deg (u) + deg (v) = |S| + |T|

= |SUT|       S∩T = ϕ

≤ n-1

But this is a contradiction to our hypothesis.

Hence our assumption is wrong. So, G is Hamiltonian.

Dirac's theorem: If G is a simple graph with 7. vertices with n ≥ 3 such that the degree of every vertex in G is at least n/2, then G has a Hamilton circuit.

A knight is a chess piece that can move either two spaces horizontally and one space vertically or one space horizontally and two spaces vertically.

That is, a knight on square (x, y) can move to any of the eight squares (x±2, y±1), (x±1, y±2), if these squares are on the chessboard, as illustrated here.

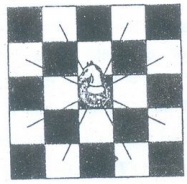
A knight's tour is a sequence of legal moves by a knight starting at some square and visiting each square exactly once. A knight's tour is called reentrant if there is a legal move that takes the knight from the last square of the tour back to where the tour began.

We can model knight's tours using the graph that has a vertex for each square on the board, with an edge connecting two vertices if a knight can legally move between the squares represented by these vertices.

A Gray code is a labelling of the arcs of the circles such that adjacent arcs are labeled with bit strings that differ in exactly one bit.

EXERCISE 3.5

1. In Kaliningrad (the Russian name for Konigsberg) there are two additional bridges, besides the seven that were present in the eighteenth century. These new bridges connect regions B and C and regions B and D, respectively. Can someone cross all nine bridges in Kaliningrad exactly once and return to the starting point?

2. Can someone cross all the briges shown in this map exactly once and return to the starting point?

3. Show that a directed multigraph having no isolated vertices has an Euler circuit if and only if the graph is weakly connected and the in-degree and out-degree of each vertex are equal.

4. Devise an algorithm for constructing Euler circuits in directed graphs.

5. For which values of n do these graphs have an Euler circuit? (a) K_n (b) C_n (c) W_n (d) Q_n

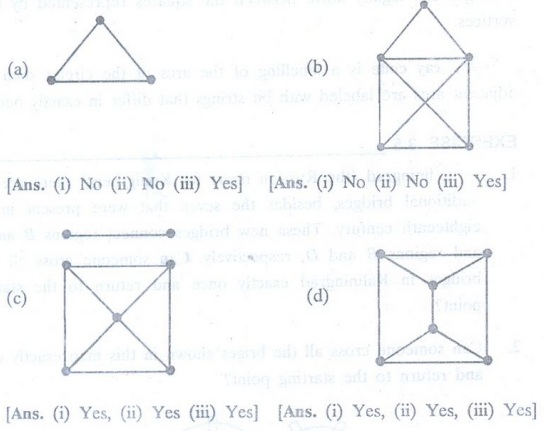
6. For each of these graphs, determine (i) whether Dirac's Theorem can be used to show that the graph has a Hamilton circuit, (ii) whether Ore's theorem can be used to show that the graph has a Hamilton circuit, and (iii) whether the graph has a Hamilton circuit.

7. Show that there is a Gray code of order n whenever n is a positive integer, or equivalently, show that the n-cube Q_n, n > 1, always has a Hamilton circuit.

[Ans. The result is trivial for n=1: code is 0 is 0, 1. Assume we have a Gray code of order n. Let C₁, …, C_k, k = 2_n be such a code. Then 0c₁,…, 0c_k, 1_ck, …, 1c₁ is a Gray code of order n+1.