Equivalence of NFA with ε to NFA without ε

Equivalence of NFA with ε to NFA without ε

AU May-04, 09, 12, Dec.-09, 12, 13, Marks 12

In this method we try to remove all the ε transitions from given NFA. The method will be

1. Find out all the ε transitions from each state from Q. That will be called as ε-closure {q} where q_i ϵ Q.

2. Then δ' transitions can be obtained. The δ' transitions means an ε-closure on δ moves.

3. Step-2 is repeated for each input symbol and for each state of given NFA.

4. Using the resultant states the transition table for equivalent NFA without & can be built.

Theorem: If L is accepted by NFA with ε transitions, then there exist L which is accepted by NFA without ε transitions. AU May-09, Marks 12; Dec.-09, 13, Marks 8

Proof :

Let, M = (Q, Σ, δ, q₀, F) be an NFA with ε transitions.

Construct M' = (Q, Σ, δ', q₀, F') where

F' = FU{q₀} if ε-closure contains state off

       F otherwise

M' is a NFA without ε moves. The δ' function can be denoted by δ" with some input. For example, δ' (q, a) = δ" (q, a) for some q in Q and a from Σ. We will apply the method of induction with input x. The x will not be ɛ because

δ' (q₀, ε) = {q₀}

8" (q₀, ε) = ε-closure (q₀). Therefore we will assume length of string to be 1.

Basis: |x| = 1. Then x is a symbol a.

δ'(q₀,a) = δ" (q₀,a)

Induction |x| > 1 Let x = wa

8'(q₀, w) = δ'(δ'(q₀, w), a)

By inductive hypothesis,

δ'(q₀, w) = δ" (q₀, w) = p

Now we will show that δ' (p, a) = δ (q₀, wa)

But

δ'(p, a) = U δ'(q, a) = U δ" (q, a)

q in p    q in p

As

p = δ" (q₀, w)

We have, U δ" (q, a) = δ" (q₀, wa)

q in p

Thus by definition δ"

δ'(q₀, wa) = δ" (q₀, wa)

Rule for conversion

δ′(q, a) = ε - closure (δ (δ (q, ε), a))

where δ(q,ε) = ε - closure (q)

Before solving some examples based on conversion of NFA with ε to NFA without ɛ above rule should be remembered.

Subset construction algorithm:

1. Initially ε - closure (q₀) is in D states of DFA.

2. While there are unmarked states q_i in D states

{

3. Marks q_i

4. for each symbol a

{

5. U = ε - closure (δ(q_i, a))

6. if (U is not in D states)

{

7. Add U as unmarked state in D states.

}

8. Dtran [q_i, a] = U

}

}

Example for Understanding

Example 1.9.1 Convert the given NFA with ɛ to NFA without ε.  AU: Dec.-09, Marks 8

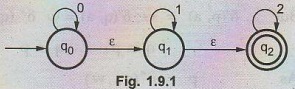
Solution: Step 1: We will first obtain ε - closure of each state i.e. we will find out ε - reachable states from current state.

Hence

ε - closure (q₀) = {q₀, q₁, q₂}

ε - closure (q₁) = {q₁, q₂}

ε - closure (q₂) = {q₂}

As ε - closure (q₀) means with null input (no input symbol) we can reach to q₀, q₁ or q₂. In a similar manner for q₁ and q₂ ε - closures are obtained.

Step 2: Now we will obtain δ' transitions for each state on each input symbol.

δ' (q₀, 0) = ε - closure (δ (δ' (q₀, ε), 0))

= ε - closure (δ(ε - closure(q₀), 0))

= ε - closure (δ(q₀, q₁, q₂), 0).

= ε - closure (δ(q₀, 0) U δ(q₁, 0) U δ (q₂,0))

= ε - closure (q₀ U ϕ U ϕ)

= ε - closure (q₀) = {q0, q1, q2}

δ' (q₀, 1) = ε - closure (δ (δ`(q₀,ε), 1))

= ε - closure (δ (q₀, q₁, q₂), 1)

= ε - closure (δ (q₀, 1) U δ (q₁, 1) U δ (q₂,1))

= ε closure (ϕ U q₁ U ϕ)

= ε - closure (q₁)

δ' (q₀, 1) = {q₁, q₂}

δ' (q₁,0) = ε - closure (δ (δ`(q₁,ε), 0))

= ε - closure (δ (ε - closure (q₁), 0))

= ε closure (δ (q₁,q₂), 0)

= ε closure (δ (q₁, 0) U δ (q₂, 0))

= ε closure (ϕUϕ)

= ε - closure (ϕ)

= ϕ

δ' (q₁, 1) = ε - closure (δ (δ` (q₁, ε), 1))

= ε - closure (δ (ε - closure (q₁), 1))

= ε - closure (δ (q₁, q₂), 1)

= ε - closure (δ (q₁, 1) U δ (q₂, 1))

= ε - closure (q₁ U ϕ)

= ε - closure (q₁)

= {q₁, q₂}

δ′(q₂, 0) = ε- closure (δ (δ` (q₂, ε), 0))

= ε - closure (δ (ε - closure (q₂), 0))

= ε - closure (δ (q₂, 0))

= ε - closure (ϕ)

= ϕ

δ ' (q₂, 1) = ε - closure (δ (δ` (q₂, ε), 1))

= ε closure (δ (ε - closure (q₂), 1))

= ε - closure (δ (q₂,1))

= ε - closure (ϕ)

δ' (q₂, 1) = ϕ

δ' (q₀, 2) = ε - closure (δ (δ` (q₂, ε), 2))

= ε - closure (δ (ε -closure (q₀), 2))

= ε - closure (δ (q₀, q₁, q₂), 2).

= ε - closure (δ (q₀, 2) U δ (q₁, 2) U δ (q₂, 2))

= ε - closure (q₂)

= ε - closure (q₂)

= {q₂}

δ' (q₁,2) = ε - closure (δ (δ` (q₁, ε), 2))

= ε - closure (δ (ε - closure (q₁), 2))

= ε - closure (δ (q₁, q₂), 2)

= &- closure (δ (q₁, 2) U δ (q₂, 2))

= ε closure (ϕ U q₂)

= {q₂}

δ′ (q₂, 2) = ε - closure (δ (δ` (q₂, ε), 2))

= ε - closure (δ (ε - closure (q₂), 2))

= ε - closure (δ (q₂, 2))

= ε - closure (q₂)

= {q₂}

Now we will summarize all the computed δ' transitions -

δ'(q₀, 0) = {q₀, q₁, q₂},   δ'(q₀, 1) = {q₁, q₂),    δ'(q₀, q₂) = {q₂}

δ'(q₁, 0) = ϕ                   δ'(q₁, 1) = {q₁, q₂},    δ'(q₁, 2) = {q₂}

δ'(q₂, 0) = ϕ                   δ'(q₂, 1) = ϕ               δ'(q₂, 2) = {q₂}     

Step 3:

From this we can write the transition table as -

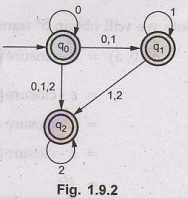
Step 4:

The NFA will be,

Here q₀, q₁ and q₂ is a final state because ε closure (q₀), ε - closure (q₁) and ε - closure (q₂) contains final state q₂.

Example 1.9.2 Convert the following NFA with e to NFA without ε.

Solution: We will first obtain ε - closure of every state. The ɛ - closure is basically an ε - transition from one state to other. Hence

ε - closure (0) = {0}

ε - closure (1) = {1}

ε - closure (2) = {2, 3, 4, 6, 9}

ε - closure (3) = {3, 4, 6}

ε - closure (4) = {4}

ε - closure (5) = {5, 8, 3, 4, 6, 9}

= {3, 4, 5, 6, 8, 9} sorted it!

ε - closure (6) = {6}

ε - closure (7) = {7, 8, 3, 4, 6, 9}

= {3, 4, 6, 7, 8, 9}

ε - closure (8) = {8, 3, 4, 6, 9}

= {3, 4, 6, 8, 9}

ε - closure (9) = {9}

Now we will obtain δ' transitions for each state and for each input symbol.

δ' (0, a) = ε - closure (δ (δ` (0, ε), a))

= ε - closure (δ (ε - closure(0), a))

= ε - closure (δ (0, a))

= ε - closure (1)

{1}

δ ' (0, b) = ε - closure (δ (δ` (0,ε), b))

= ε - closure (δ (ε - closure (0), b))

= ε - closure (δ (0, b))

= ε - closure (ϕ)

= ϕ

δ' (1,a) = ε - closure (δ (δ` (1,ɛ), a))

= ε - closure (δ (ε - closure (1), a))

= ε - closure (δ (1, a))

= ε - closure (ϕ)

= ϕ

δ ' (1, b) = ε - closure (8 (8 (1,ε), b))

= ε - closure (δ (ε - closure (1), b))

= ε - closure (δ (1, b))

= ε - closure (2)

= {2, 3, 4, 6, 9}

δ ' (2, a) = ε - closure (δ (δ` (2,ε), a))

= ε - closure (δ (ε - closure (2), a))

= ε - closure (δ (2, 3, 4, 6, 9), a)

= ε - closure (δ (2, a) U δ (3, a) U δ (4, a) U δ (6, a) U δ (9, a))

= ε - closure (ϕ U ϕ U 5 U ϕ U ϕ )

= ε - closure (5)

= {3, 4, 5, 6, 8, 9}

δ' (2, b) = ε - closure: (δ (δ (2, ε), b))

= ε - closure (δ (ε - closure (2), b))

= ε - closure (δ (2, 3, 4, 6, 9), b)

= ε - closure (δ(2, b) U δ(3, b) U δ(4, b) U δ(6, b) U δ(9, b))

= ε - closure (ϕ U ϕ U ϕ U 7 U ϕ)

= ε - closure (7)

= {3, 4, 6, 7, 8, 9}

δ'(3, a) = ε - closure (δ (δ'(3,ε), a))

= ε - closure (δ (ε - closure (3), a))

= ε - closure (δ (3, 4, 6), a).

= ε - closure (δ (3, a) U δ (4, a) U δ (6, a))

= ε - closure (ϕ U 5 U ϕ)

= ε - closure (5)

= {3, 4, 5, 6, 8, 9}

δ`(3, b) = ε - closure (δ (δ`(3, ε), b))

= ε - closure (δ (ε - closure (3), b))

= ε - closure (δ (3, 4, 6), b)

= ε - closure (δ (3, b) U δ (4, b) U δ (6, b))

= ε - closure (ϕ U ϕ U 7)

= ε - closure (7)

= {3, 4, 6, 7, 8, 9}

δ` (4, a) = ε - closure (δ (δ` (4, ε), a))

= ε - closure (δ (ε - closure (4), a))

= ε - closure (δ (4, a))

= ε - closure (5)

= {3, 4, 5, 6, 8, 9}

δ`(4, b) = ε - closure (δ (δ` (4, ε), b))

= ε - closure (δ (ε - closure (4, b))

= ε - closure (δ (4, b))

= ε - closure (ϕ)

= ϕ

δ ' (5, a) = ε - closure (δ (δ`(5, ε), a))

= ε - closure (δ (ε - closure (5), a))

= ε - closure (δ (3, 4, 5, 6, 8, 9), a)

= e-closure (δ (3, a) U (4, a) U δ (5, a) U δ (6, a) U δ (8, a) U δ (9,a))

= ε - closure (ϕ U 5 U ϕ U ϕ U ϕ U ϕ U ϕ)

= ε - closure (5)

= {3, 4, 5, 6, 8, 9}

δ' (5, b) = ε - closure (δ (δ`(5, ε), b))

= ε - closure (δ (ε - closure (5), b))

= ε - closure (δ (3, 4, 5, 6, 8, 9), b)

= ε - closure (δ (3, b) U δ (4, b) U δ (5, b) U δ (6, b) U δ (8, b) U δ (9, b))

= ε - closure (ϕ U ϕ U ϕ U 7 U ϕ U ϕ)

= ε - closure (7)

= {3, 4, 6, 7, 8, 9}

δ' (6, a) = ε - closure (δ (δ` (6, ɛ), a))

= ε - closure (δ (ε - closure (6), a))

= ε - closure (δ (6, a))

= ε - closure (ϕ)

= ϕ

8' (6, b) = ε - closure (δ (δ (6, ɛ), b))

= ε - closure (δ (ε - closure (6), b))

= ε - closure (δ (6, b))

= ε - closure (7)

= {3, 4, 6, 7, 8, 9}

δ' (7, a) = ε - closure (δ (δ`(7, ε), a))

= ε - closure (δ (ε - closure (7), a))

= ε - closure (δ (3, 4, 6, 7, 8, 9), a)

= ε - closure (δ (3, a) U δ (4, a) U δ (6, a) U δ (7, a) U δ (8, a) U δ (9, a))

= ε - closure (ϕ U 5 U ϕ U ϕ U ϕ U ϕ)

= ε - closure (5)

= {3, 4, 5, 6, 8, 9}

δ ' (7, b) = ε - closure (δ (δ` (7, ε), b))

= ε - closure (δ (ε - closure (7), b))

= ε - closure (δ (3, 4, 6, 7, 8, 9), b)

= ε - closure (δ (3, b) U δ (4, b) U δ (6, b) U δ (7, b) U δ (8, b) U δ (9, b))

= ε - closure (ϕ U ϕ U 7 U ϕ U ϕ U ϕ)

= ε - closure (7)

= {3, 4, 6, 7, 8, 9}

δ' (8, a) = ε - closure (δ (δ`(8, ε), a))

= ε - closure (δ (ε - closure (8), a))

= ε - closure (δ (3, 4, 6, 8, 9), a)

= ε - closure (δ (3, a) U δ (4, a) U δ (6, a) U δ (8, a) U δ (9, a))

= ε - closure (ϕ U 5 U ϕ U ϕ U ϕ)

= ε - closure (5)

= {3, 4, 5, 6, 8, 9}

δ' (8, b) = ε - closure (δ (δ` (8, ε), b))

= ε - closure (δ (ε - closure (8), b))

= ε - closure (δ (3, 4, 6, 8, 9), b)

= ε - closure (δ (3, b) U δ (4, b) U δ (6, b) U δ (8, b) U δ (9, b))

= ε - closure (ϕ U ϕ U 7 U ϕ U ϕ)

= ε - closure (7)

= {3, 4, 6, 7, 8, 9}

δ' (9, a) = ε - closure (δ (δ` (9, ε), a))

= ε - closure (δ (ε - closure (9), a))

= ε - closure (δ (9, a))

= ε - closure (ϕ)

= ϕ

δ' (9, b) = ε - closure (δ (δ` (9, ε), b))

= ε - closure (δ (ε - closure (9), b))

= ε - closure (δ (9, b))

= ε - closure (ϕ)

= ϕ

Now we will build the transition table using above calculated δ' transitions.

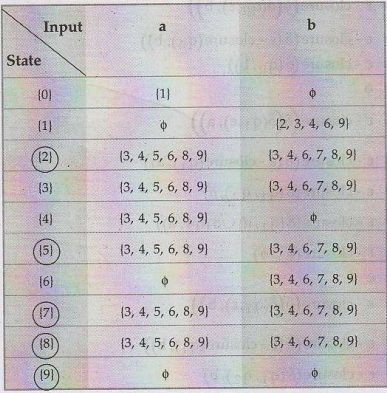
State {2} is a final state since ε - closure (2) contains 9 which is actually a final state in given NFA. Similarly state 5, 7, 8 and 9 are final states.

Example 1.9.3 Convert the following NFA with & to NFA without ɛ.

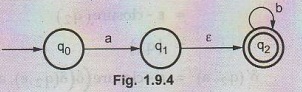
Solution: We will first obtain & - closures of q₀, q₁ and q₂ as follows.

ε - closure (q₀) = {q₀}

ε - closure (q₁) = {q₁, q₂}

ε - closure (q₂) = {q₂}

Now the δ' transitions on each input symbol is obtained as,

8' (q₀, a) = ε - closure (δ (δ` (q₀, ε), a))

= ε - closure (δ (ε - closure (q₀), a))

= ε - closure (δ (q₀, a))

= ε - closure (q₁)

= {q₁, q₂}

δ' (q₀, b) = ε - closure (δ (δ` (q₀, ε), b))

= ε - closure (δ (ε - closure (q₀), b))

= ε - closure (δ (q₀, b)).

= ϕ

δ' (q₁, a) = ε - closure (δ (δ` (q₁, ε), a))

= ε - closure (δ (ε - closure (q₁), a))

= ε - closure (δ (q₁, q₂), a)

= ε - closure (δ (q₁, a) U δ (q₂, a))

= ε - closure (ϕ U ϕ)

= ϕ

δ' (q₁, b) = ε - closure (δ (δ` (q₁, ε), b))

= ε - closure (δ (ε - closure (q₁), b))

= ε - closure (δ (q₁, q₂), b)

= ε - closure (δ (q₁, b) U δ (q₂, b))

= ε - closure (q₂)

= ε - closure (q₂)

= {q₂}

δ' (q₂, a) = ε - closure (δ (δ` (q₂, ε), a))

= ε - closure (δ (ε - closure (q₂), a))

= ε - closure (δ (q₂, a))

= ε - closure (ϕ)

= ϕ

δ' (q₂, b)

= ε - closure (δ (δ`(q₂, ε), b))

= ε - closure (δ (ε - closure (q₂), b))

= ε - closure (δ (q₂, b))

= ε - closure (q₂)

= {q₂}

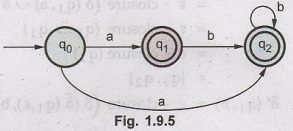
The transition table can be –

States q₁ and q₂ becomes the final as closures of q₁ and q₂ contains the final state q₂. The NFA can be shown by transition diagram as shown in Fig. 1.9.5.

Example 1.9.4 Convert the given NFA with ɛ to ordinary NFA.

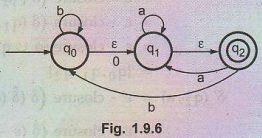
Solution: We will first obtain ε - closure of each state.

ε - closure (q₀) = {q₀, q₁, q₂}

ε - closure (q₁) = {q₁, q₂)

ε - closure (q₂) = {q₂}

Now &' transitions for each state on each input.

8' (q₀, a) = ε - closure (δ (δ` (q₀, ε), a))

= ε - closure (δ (ε - closure (q₀), a))

= ε closure (δ ((q₀, q₁, q₂), a))

= ε closure (δ (q₀, a) U δ (q₁, a) U δ (q₂, a))

= ε - closure (ϕ U q₁ U q₁).

= ε - closure (q₁)

= (q₁, q₂)

δ' (q₀, b) = ε - closure (δ (δ` (q₀, ε), b))

= ε closure (δ (ε - closure (q₀), b))

= ε - closure (δ ((q₀, q₁, q₂), b))

= ε - closure (δ (q₀, b) U δ (q₁, b) U δ (q₂, b))

= ε - closure (q₀ U ϕ U q₀)

= ε - closure (q₀)

= (q₀, q₁, q₂)

δ' (q₁, a) = ε - closure (δ (δ` (q₁, ε), a))

= ε - closure (δ (ε - closure (q₁), a))

= ε - closure (δ ({q₁, q₂), a))

= ε - closure (δ (q₁, a) U δ (q₂, a))

= ε - closure (q₁ U q₁)

= ε - closure (q₁)

= {q₁, q₂}

δ' (q₁, b) = ε - closure (δ (δ` (q₁, ε), b))

= ε - closure (δ (ε - closure (q₁), b))

= ε - closure (δ (q₁, q₂), b))

= ε - closure (δ (q₁, b) U δ (q₂, b))

= ε closure (ϕ U q₀)

= {q₀, q₁, q₂}

δ' (q₂, a) = ε - closure (δ (δ` (q₂, ε), a))

= ε - closure (δ (ε - closure (q₂), a))

= ε - closure (δ (q₂, a))

= ε - closure (q₁)

= (q₁, q₂)

δ' (q₂, b) = ε - closure (δ (δ` (q₂, ε), b))

= ε closure (δ (ε - closure (q₂), b))

= ε - closure (δ (q₂, b))

= ε - closure (q₀)

= {q₀, q₁, q₂}

The transition table can be –

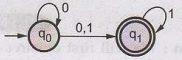
Example 1.9.5 Construct an NFA without ε transitions for the NFA given in Fig. 1.9.7.       AU May-12, Marks 8

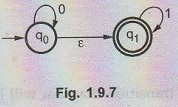
Solution: We will first obtain ε - closures of q₀ and q₁ as follows -

ε - Closure (q₀) = {q₀, q₁}

ε - Closure (q₁) = {q₁}

Now δ' transitions on each input symbol is obtained as -

δ'(q₀, 0) = ε - Closure (δ (δ` (q₀, ε), 0))

= ε - Closure (δ (ε - Closure (q₀), 0))

= ε - Closure (δ ((q₀, q₁), 0))

= ε - Closure (q₀)

δ' (q₀, 0) = {q₀, q₁}

δ' (q₀, 1) = ε - Closure (δ (δ` (q₀, ε), 1))

= ε - Closure (δ (ε - Closure (q₀), 1))

= ε - Closure (8 ((q₀, q₁), 1))

= ε - Closure (q₁)

δ' (q₀, 1) = {q₁}

δ' (q₁, 0) = ε - Closure (δ (δ` (q₁, ε), 0))

= ε - Closure (δ (ε - Closure (q₁), 0))

= ε - Closure (δ (q₁, 0))

= ε - Closure (ϕ)

δ' (q₁, 0) = ϕ

δ' (q₁, 1) = ε - Closure (δ (δ` (q₁, ε), 1))

= ε - Closure (δ (ε - Closure (q₁), 1))

= ε - Closure (δ (q₁, 1))

= ε - Closure (q₁)

δ' (q₁, 1) = {q₁}

The transation table for NFA without & will be,

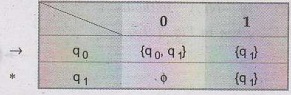
The transition diagram will be -

Review Question

1. If L is accepted by a NFA with & transition then show that L is accepted by an NFA without ε transition.

AU: May-04, Dec.-09, Marks 8; May-09, Marks 12, Dec.-12, Marks 8