Equivalence of NFA with ε to DFA

Equivalence of NFA with ε to DFA

AU: May-05, 11, Dec.-06,13,15,18, Marks 16

Prove that there exists a DFA for every ε - NFA.

AU: May-11, Marks 8

Step 1: Consider M = (Q, Σ, δ, q₀, F) is a NFA with ε. We have to convert this NFA with ε to equivalent DFA denoted by

M_D = (Q_D, Σ, δ_D, q₀, F_D)

Then obtain,

ε - closure (q₀) = {P₁, P₂, P₃... P_n} then [P₁, P₂, P₃ ,... P_n] becomes a start state of DFA.

Now [P₁, P₂, P₃... P_n] ϵ Q_D

Step 2: We will obtain δ transitions on [P₁, P₂, P₃, ... P_n ] for each input.

δ_D ([P₁, P₂, P_n], a) = ε - closure (δ (P₁, a) U δ (P₂, a) U... δ (P_n, a))

= Uⁿ_i=1 ε - closure d (P_i, a)

where a is input ϵ Σ.

Step 3: The states obtained [P₁, P₂, P₃, ... P_n] ϵ Q_D. The states containing final state P_i is a final state in DFA.

Now let us see some examples of conversion based on this procedure.

Example 1.11.1 Convert the following NFA with ε to equivalent DFA.

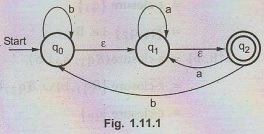
Solution: 

Step 1: To convert this NFA we will first find ɛ-closures.

ε - closures {q₀} = {q₀, q₁, q₂}

ε - closures {q₁} = {q₁, q₂}

ε - closures {q₂} = {q₂}

Step 2: Let us start from ε - closure of start state

ε - closure {q₀} = {q₀, q₁, q₂} we will call this state as A.

Now let us find transitions on A with every input symbol.

δ (A, a) = ε-closure (δ (A, a))

= ε - closure (δ (q₀, q₁, q₂), a)

= ε - closure {(q₀, a) U δ (q₁, a) U δ (q₂, a)}

= ε - closure {q₁}

= {q₁, q₂). Let us call it as state B.

δ (A, b) = ε-closure (δ (A, b))

= ε - closure (δ (q₀, q₁, q₂), b)

= ε - closure {δ (q₀, b) U δ (q₁, b) U δ (q₂, b)}

= ε - closure {q₀}

= {q₀, q₁, q₂} i.e. A.

Hence we can state that,

δ' (A, a) = B

δ` (A, b) = A

Step 3: Now let us find transitions for state B = {q₁, q₂}

δ' (B, a) = ε - closure (δ (q₁, q₂), a)

= ε - closure {q₁}

= {q₁, q₂} i.e. B

δ` (B, b) = ε - closure (δ (         q₁, q₂), b)

= ε - closure {δ (q₁, b) U δ (q₂, b)}

= ε - closure {q₀}

= (q₀, q₁, q₂) i.e. A.

Step 4: Hence the generated DFA is

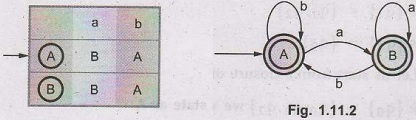
Example 1.11.2 Convert the given NFA into its equivalent DFA -

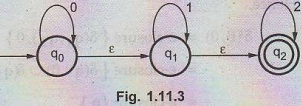
Solution: Let us obtain ε - closure of each state.

ε - closure (q₀) = {q₀, q₁, q₂}

ε - closure (q₁)= {q₁, q₂}

ε - closure (q₂) = {q₂}

Now we will obtain d' transition. Let e-closure (q₀) = {q₀, q₁, q₂} call it as state A.

δ' (A, 0) = ε - closure { δ ((q₀, q₁, q₂), 0)}

= ε - closure {δ (q₀, 0) U δ (q₁, 0) U δ (q₂, 0)}

= ε - closure {q₀}

= {q₀, q₁, q₂} i.e. state A

 δ' (A, 1) = ε - closure { δ ((q₀, q₁, q₂), 1)}

= ε - closure {(q₀,1) U δ (q₁,1) U δ (q₂,1)}

= ε - closure {q₁, q₂}

= {q₁, q₂} Call it as state B

δ' (A, 2) = ε - closure {δ ((q₀, q₁, q₂), 2)}

= ε - closure {δ (q₀, 2) U δ (q₁, 2) U δ (q₂, 2)}

= ε - closure {q₂}

= {q₂} Call it as state C.

Thus we have obtained,

δ` (A, 0) = A

δ` (A, 1) = B

δ` (A,2) = C

i.e.

Now we will find transitions on states B and C for each input.

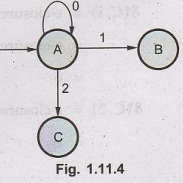
Hence,

δ' (B, 0) = ε - closure {δ (q₁, q₂), 0}

= ε - closure {δ (q₁, 0) U δ (q₂, 0)}

= ε - closure {ϕ}

= ϕ

δ' (B, 1) = ε - closure {δ (q₁, q₂), 1}

= ε - closure {δ (q₁, 1) U δ (q₂, 1)}

= ε - closure {q₁}

= {q₁, q₂) i.e state B itself.

δ` (B, 2) = ε - closure {δ (q₁, q₂), 2}

= ε - closure {δ (q₁, 2) U δ (q₂, 2)}

= ε - closure {q₂}

= {q₂} i.e state C.

Hence,

δ` (B, 0) = ϕ

δ` (B, 1) = B

δ` (B, 2) = C

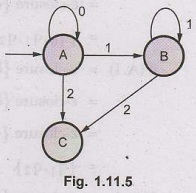
The partial transition diagram will be,

Now we will obtain transitions for C:

δ` (C, 0) = ε - closure {δ (q₂, 0)}

= ε - closure {ϕ}

= ϕ

δ` (C, 1) = ε - closure {δ (q₂, 1)}

= ε - closure {ϕ}

= ϕ

δ` (C,2) = ε - closure {δ (q₂, 2)}

= q₂

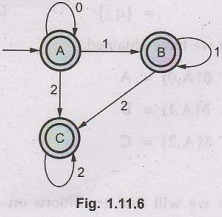
Hence the DFA is,

As A = {q₀, q₁, q₂} in which final state q₂ lies hence A is final state in B = {q₁, q₂} the state q₂ lies hence B is also final state in C = {q₂}, the state q₂ lies hence C is also a final state.

Example 1.11.3 Consider following NFA with ε.

AU: May-11, Marks 6

Convert it to its equivalent DFA.

Solution: We will first compute ε - closure for start state p.

ε closure (p) = {p} call it as state A.

Now we will obtain 8 transitions on state A.

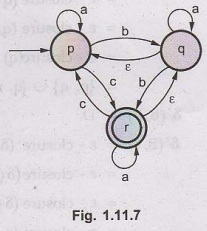
State A

δ' (A, a) = ε - closure (δ (A, a))

= ε - closure (δ (p, a))

= ε - closure (p)

= {p} i.e. state A only.

δ' (A, b) = ε - closure (δ (A, b))

= ε - closure (δ (p, b))

= ε - closure (q)

= {q, p} i.e. {p, q} Let us call it state B.

δ' (A, b) = B

δ' (A, c) = ε - closure (δ (A, c))

= ε - closure (δ (p, c))

= ε - closure (r) = {q, r} Call it as state C.

State B = {p, q}

δ' (B, a)

= ε - closure (δ (B, a))

= ε - closure (δ (p, q), a)

= ε - closure (δ (p, a) U δ (q, a))

= ε - closure (p U q)

= ε - closure (p, q)

= ε - closure(p) Ụ ɛ - closure(q)

= {P} U {q} = {p, q} i.e. state B only.

δ' (B, a) = B.

δ' (B, b) = ε - closure (δ (B, b))

= ε - closure (δ (p, q), b)

= ε - closure (δ (p, b) U δ (q, b))

= ε - closure (q U r)

= ε - closure (q, r)

δ' (B, b) = ε - closure(q) U ε - closure(r)

= {p, q} U {q, r} = {p, q, r} i.e. state D

δ`(B, b) = D.

δ' (B, c) = ε - closure (δ (B, C))

= ε - closure (δ (p, q), c)

= ε - closure (δ (p, c) U δ (q, c))

= ε - closure (r U ϕ)

= ε - closure (r)

= {q, r}

δ' (B, c) = C

State C = {q, r}

δ' (C, a) = ε - closure (δ (C, a))

= ε - closure (δ (q, r), a)

= ε - closure (δ (q, a) U δ (r, a))

= ε - closure (q U r)

= ε - closure (q) U ε - closure(r)

= {p, q} U {q, r}

= (p, q, r) i.e. state D.

δ' (C, a) = D

8' (C, b) = ε - closure (δ (C, b))

= ε - closure (δ (q, r), b)

= ε - closure (δ (q, b) U δ (r, b)).

= ε - closure (r U ϕ)

= ε - closure (r)

= {q, r) i.e. state C.

δ' (C, b) = C

δ' (C, c) = ε - closure (δ (C, c))

= ε - closure (δ (q, r), c)

= ε - closure (δ (q, c) U δ (r, c))

= ε - closure (ϕ U p)

= ε - closure (p)

= {p} i.e. state A.

δ' (C, c) = A

State D = {p, q, r}

δ' (D, a) = ε - closure (δ (D, a))

= ε - closure (δ (p, q, r), a)

= ε - closure (δ (p, a) U δ (q, a) U δ (r, a))

= ε - closure (p U q U r)

= ε - closure (p) U ɛ - closure(q) U ε - closure (r)

= (p, q, r) i.e. state D.

δ ' (D, a) = D

8' (D, b) = ε - closure (δ (D, b))

= ε - closure (δ (p, q, r), b)

= ε - closure (δ (p, b) U δ (q, b) U δ (r, b))

= ε - closure (q U r U ϕ)

= ε - closure (q, r)

= ε - closure (q) U ε - closure (r)

= (p, q, r) i.e. state D.

δ' (D, b) = D

δ' (D, c) = ε - closure (δ (D, c))

= ε - closure (δ (p, q, r), c)

= ε - closure (δ (p, c) U δ (q, c) U δ (r, c))

= ε - closure (r U ϕ U p)

= ε - closure (r) U ε - closure (p)

= {q, r} U {P}

= {p, q, r} i.e. state D.

δ' (D, c) = D

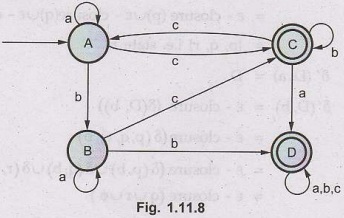
The transition table from above calculations can be obtained as,

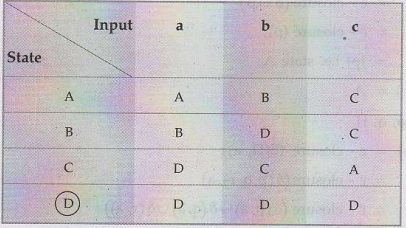
As state A = {p} it is a start state and states C and D contain final state r, hence these are final states. The transition diagram for the DFA is,

Example 1.11.4 Consider the following ε - NFA for an identifier. Consider the ε -closure of each state and find it's equivalent DFA. AU: Dec.-15, Marks 10

Solution:

ε - closure (1) = {1}  Call it as state A

δ' (A, letter) = ε - closure(δ (1, letter)

= ε - closure(2)

= {2, 3, 4, 5, 8, 10}   Call it as state B

δ' (A, letter) = B

δ' (A, digit) = ε - closure(δ (1, digit))

= ϕ

δ' (A digit) = ϕ

δ' (B, letter) = ε - closure(δ (2, 3, 4, 5, 8, 10), letter)

= ε – closure (6)

= {6, 7, 4, 5, 8, 10) i.e.

= {4, 5, 6, 7, 8, 10}   Call it as state C

δ' (B, letter) = C

δ' (B, digit)   = ε - closure(&(2, 3, 4, 5, 8, 10), digit)

= ε – closure (9)

= {9, 7, 4, 5, 8, 10} i.e.

= {4, 5, 7, 8, 9, 10}   Call it as state D

δ' (B, digit) = D

δ' (C, letter) = ε - closure(δ (4, 5, 6, 7, 8, 10), letter)

= ε – closure (6)

= C

δ' (C, letter) = C

δ' (C, digit) = ε - closure(δ (4, 5, 6, 7, 8, 10), digit)

= ε – closure (9)

= D

δ' (C, digit) = D

δ' (D, letter) = ε - closure(δ (4, 5, 7, 8, 9, 10), letter)

= ε - closure (6)

= C

δ' (D, letter) = C

δ' (D, digit) = ε - closure(δ (4, 5, 7, 8, 9, 10), digit)

= ε - closure (9)

= D

δ' (D, digit) = D

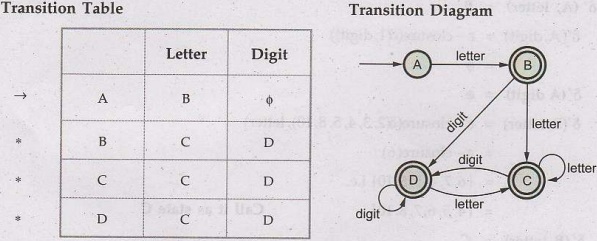
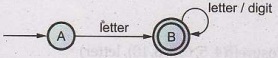
The two states C and D are equivalent. Similarly state B and C are equivalent

B = C = D.

The minimized DFA will then be

Example 1.11.5 Convert the following ε - NFA to NFA and then convert the resultant NFA to DFA.

AU Dec.-18, Marks 13

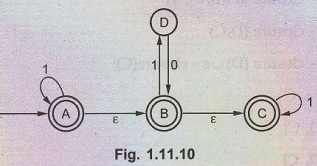
Solution: Conversion of NFA to NFA

We will obtain ɛ - closure of each state

ε - closure (A) = {A, B, C}

ε - closure (B) = {B, C}

ε - closure (C) = {C}

ε - closure (D) = {D}

Now we will obtain δ' transitions for each state on each input symbol.

δ' (A, 0) = ε - closure (δ (ε - closure(A), 0))

= ε - closure (δ ((A, B, C), 0))

= ε - closure (δ (A, 0) U δ (B, 0), U δ (C,0))

= ε - closure (ϕ U ϕ U ϕ)

= ϕ

δ' (A, 0) = ϕ

δ' (A, 1) = ε - closure (δ (ε - closure(A), 1))

= ε - closure (δ (A, B, C), 1)

= ε - closure (A, D, C)

= ε - closure (A) U ε - closure (D) U ε - closure (C)

= {A, B, C, D}

δ' (A, 1) = {A, B, C, D}

δ' (B, 0) = ε - closure (δ (ε - closure (B), 0))

= ε - closure (δ (B, C), 0)

δ' (B, 0) = ϕ

δ' (B, 1) = ε - closure (δ (ε - closure (B), 1))

= ε - closure (δ ((B, C), 1)

= ε - closure (D, C)

= ε - closure (D) U ε - closure(C)

= D U C

= {D, C}

δ' (B, 1) = {D, C}

δ' (C, 0) = ε - closure(δ (ε - closure(C), 0)

= ε - closure (δ (C, 0)

= ε - closure (ϕ)

δ' (C, 0) = ϕ

δ' (C, 1) = ε - closure (δ (ε - closure (C), 1)

= ε - closure (δ (C, 1)

= ε - closure (C)

= {C}

δ' (C, 1) = C

δ' (D, 0) = ε closure (δ (ε - closure(D), 0))

= ε - closure (δ (D, 0)

= ε - closure (B)

δ' (D, 0) = (B, C)

δ' (D, 1) = ε - closure (8 (e-closure(D), 1))

= ε - closure (δ (D, 1)

= ε - closure (ϕ)

δ' (D, 1) = ϕ

The transition table will be

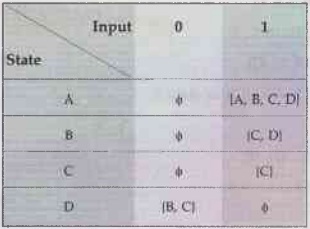
The NFA will be:

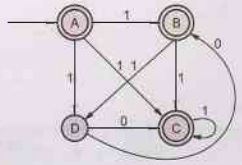
Conversion of NFA to DFA

δ (A, 0) = 0

δ (A, 1) = {A, B, C, D} → call it as state P

δ (A, 1) = p

δ (P, 0) = P

= δ ((A, B, C, D), 0)

= δ (A, 0) U δ (B, 0) U δ (C, 0) U δ (D, 0)

{B, C} → call it as state Q

S (P, 0) = Q

δ (P, 1) = δ ((A, B, C, D), 1)

= δ (A, 1) U δ (B, 1) U δ (C, 1) U δ (D, 1)

= {A, B, C, D}

δ (P,1) = P

δ (Q, 0) = δ ((B, C,), 0)

= δ (B, 0) U δ (C, 0)

δ (Q, 0) = ϕ

δ (Q, 1) = ((B, C), 1)

= δ (B, 1) U δ (C, 1)

= {C, D} U {C}

= {C, D} → call it as state R

δ (Q, 1) = R

δ (R, 0) = {δ (C, D), 0}

= {B, C}

δ (R, 0) = Q

δ (R, 1) = δ ((C, D), 1)

δ (R, 1) = {C}

δ (C, 0) = ϕ

δ (C, 1) = C

The transition table will be

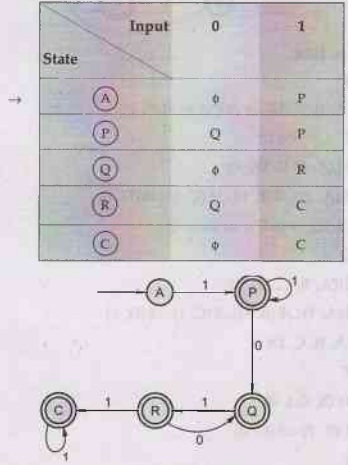
Review Questions

1. Let L be a set accepted by NFA then prove that there exists a deterministic finite automaton that accepts L. Is the converse true? AU: May-05, Marks 10

2. Prove that a language L is accepted by some ε - NFA if and only if L is accepted by some DFA. AU: Dec.-06, Marks 8

3. Prove the equivalence of NFA and DFA using subset construction. AU: Dec.-13, Marks 8