Equivalence of NFA and Regular Expression

Equivalence of NFA and Regular Expression

AU: May-04,06,09,10,11,12,14,16,17, Dec.-10,14,15,19, Marks 10

Theorem 1: Let r be a regular expression, then there exists a NFA with ε transitions that accepts L (r).

Proof: This theorem can be proved by induction method.

The basis of induction will be by considering r has zero operators.

Basis (zero operators) - Now, since r has zero operators, means r can be either ε or ϕ or a for some a in input set Σ.

The finite automata for the same can be written as

Induction: This theorem can be true for n number of operators. The n is greater than or equal to 1. The regular expression contains equal to or more than one operators.

In any type of regular expression there are only three cases possible.

1. Union 2. Concatenation 3. Closure

Let us see each,

Case 1: Union case

Let r = r₁ + r₂ where r₁ and r₂ be the regular expressions.

There exists two NFA's M₁ = (Q₁, Σ₁, δ₁, {f         ₁})

and M₂ = (Q₂, Σ₂, δ₂,{f₂})

L (M₁) = L(r₁) means the language states by regular expression r₁ is same which is represented by M₁. Similarly L (M₂) = L (r₂).

Q₁ represents the set of all the states in machine M₁.

Q₂ represents the set of all the states in machine M₂.

We assume that Q₁ and Q₂ are totally different i.e. Q₁ and Q₂ are disjoint.

Let q₀ be new initial state and f₀ be the new final state we will form

M = ((Q₁ U Q₂ U {q₀, f₀}), (Σ₁ U Σ₂), δ, q₀ {f₀})

The δ is denoted by,

i) δ (q₀, ε) (q₁, q₂}

ii) δ (q, a) = δ₁ (q, a) for q in Q₁ - {f₁} and a in Σ₁ U {E}.

iii) δ (q, a) = δ₂ (q, a) for q in Q₂ -{f₂} and a in Σ₂ U {E}.

iv) δ (f₁, ε) = δ₁ (f₂, ε) = {f₀}

All the moves are now present in machine M which is as shown Fig. 2.3.2.

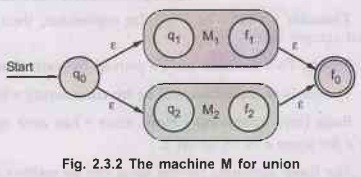
The construction of machine M is shows the transition from q₀ to f₀ must begin by going to q₁ or q₂ on ε. If the path goes to q₁, then it follows the path in machine M₁ and goes to the state f₁ and then to f₀ on ε. Similarly, if the path goes to q₂, then it follows the path in machine M₂ and goes to state f₂ and then to f₀ on ε. Thus the L (M) = L (M₁) U L (M₂). That means either the path in machine M₁ or M₂ will be followed.

Case 2: Concatenation case

Let, r = r₁ r₂ where г₁ and r₂ are two regular expressions. The M₁ and M₂ denotes the two machines such that L (M₁) = L (r₁) and L (M₂) = L (r₂).

The construction of machine M will be

M = (Q₁ U Q₂, Σ₁ U Σ₂, δ,{q₁}, {f₂})

The mapping function δ will be given as

i) δ (q, a) = δ₁ (q, a) for q in

Q₁ - {f₁} and α in Σ₁ U{ε}

ii) δ (f₁, ε) = {q₂}.

iii) δ (q, a) = δ₂ (q, a) for q in

Q₂ and a in Σ₁ U {ε}

The machine M is shown in the Fig. 2.3.3.

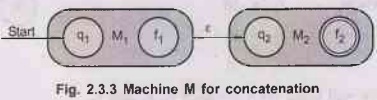
The initial state is q₁ by some input a the next state will be f₁. And on receiving ε the transition will be from f₁ to q₂ and the final state will be f₂. The transition from q₂ to f₂ will be on receiving some input b.

Thus L (M) = ab

That is a is in L (M₁) and b is in L (M₂).

Hence we can prove L (M) = L (M₁) L (M₂).

Case 3: Closure case

Let r = r₁ where r₁ be a regular expression.

The machine M₁ is such that L(M₁)=L(r₁).

Then construct M = (Q₁ U {q₀, f₀}, Σ₁, δ, q₀, {f₀}).

The mapping function δ is given

by,

i) δ (q₀, ε) = δ (f₁, ε) = {q₁, f₀}

ii) δ (q, a) = δ₁ (q, a) for q in

Q₁ - {f₁} and a in Σ₁ U {ε}

The machine M will be

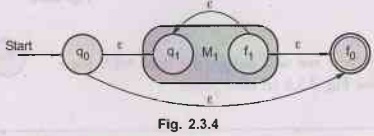
The machine M₁ shows that from q₀ to q₁ there is a transition on receiving ε similarly, from q₀ to f₀ on & there is a path. The path exists from f₁ to q₁, a back path. Similarly a transition from f₁ to f₀ final state, on receiving ε. The total recursion is possible. Thus one can derive ɛ, a, aa, aaa, .... for the input a.

Thus L (M) = L (M₁)* is proved.

Now based on this proof let us solve some examples. These examples illustrate how to convert given regular expression to NFA with ɛ moves.

Example 2.3.1 Construct an NFA equivalent to the following regular expression

((10) + (0+1)*) 01.     AU: May-06, Marks 10

Solution: Consider

r.e. = (r₁ + r₂) r₃

where

r₁ = 10

r₂ = (0+1)*

r₃ = 01

We will build NFA for each r₁, r₂ and r₃.

r₁ = 10

r₂ = (0+1)*

r₃ = 01

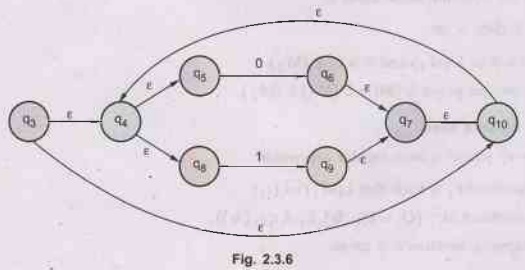
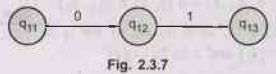
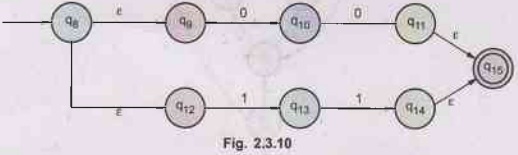
Now we will design the final NFA for r. (See Fig. 2.3.8 on next page)

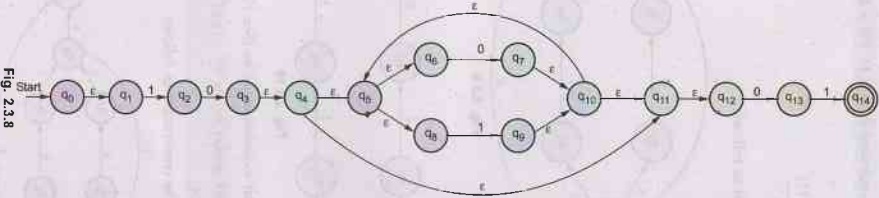
(I+00) (1+0) = 97

Example 2.3.2 Construct a NFA equivalent to (0 + 1)* (00 + 11). AU May-04, Marks 8

Solution: Consider

r.e. = (0 + 1)* (00 + 11)

r₁ = (0 + 1)

r₂ = (00 + 11)

The NFA for r₁ can be drawn as follows.

The NFA for r₂ can be

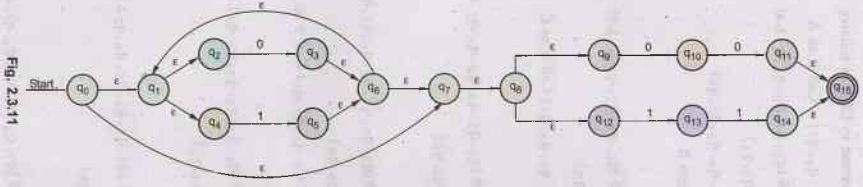
The NFA for the given regular expression can be (See Fig. 2.3.11 on next page).

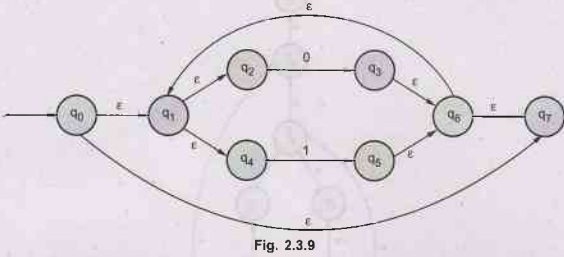
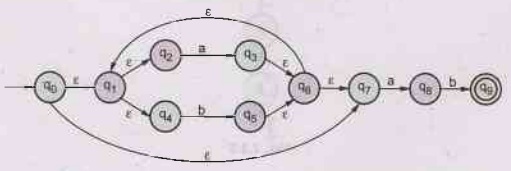
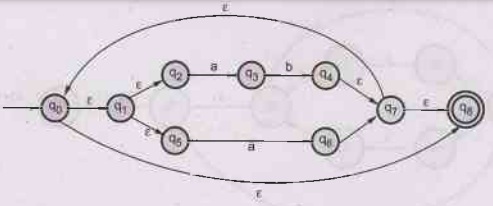
Example 2.3.3 Construct NFA with epsilon for the RE = (a|b)* ab and convert into DFA and further find the minimized DFA.   AU May-17, Marks 16

Solution: The NFA with ɛ can be constructed as follows

The above NFA can be converted to DFA as follows -

ε - closure (q₀) = {q₀, q₁, q₂, q₄, q₇} = Call it as A

δ' (A, a) = ε - closure (δ (q₀, q₁, q₂, q₄, q₇), a)

= ε - closure (q₃, q₈)

= {q₁, q₂, q₃, q₄, q₆, q₇, q₈}

δ' (A, a) = Call it as state B

δ' (A, a) = B

δ' (A, b) = ε - closure (δ (q₀, q₁, q₂, q₄, q₇), b)

= ε - closure (q₅)

= {q₁, q₂, q₄, q₅, q6, q₇} Call it as C

δ' (A, b) = C

δ' (B, a) = ε - closure (δ (q₁, q₂, q₃, q₄, q₆, q₇, q₈), a)

= ε - closure (q₃, q₈)

δ' (B, a) = B

δ' (B, b) = ε - closure (δ (q₁, q₂, q₃, q₄, q₆, q₇, q₈), b)

= ε - closure (q₅, q₉)

= {q₁, q₂, q₄, q₅, q₆, q₇, q₉} Call it as D

δ' (B, b) = D

δ' (C, a) = ε - closure (δ (q₁, q₂, q₄, q₅, q₆, q₇), a)

= ε - closure (q₃, q₈)

δ' (C, a) = B

δ' (C, b) = ε - closure (δ (q₁, q₂, q₄, q₅, q₆, q₇), b)

= ε - closure (q₅)

δ' (C, b) = C

δ' (D, a) = - closure (δ (q₁, q₂, q₄, q₅, q₆, q₇, q₉), a)

= ε - closure (q₃, q₈)

δ' (D, a) = B

δ' (D, b) = δ - closure (δ (q₁, q₂, q₄, q₅, q₆, q₇, q₉), b)

= ε - closure (q₅, q₉)

δ' (D, b) = D

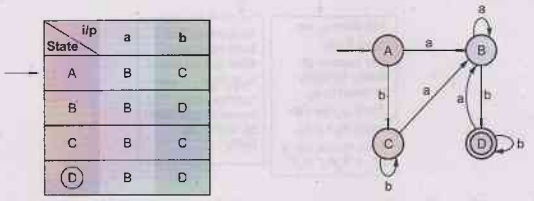
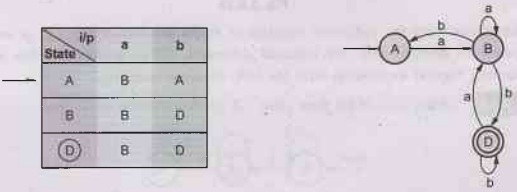
As no new state is getting generated the transition table will be

The δ transition of state B and state D is same but B is a non final state while D is a final state. So we can not merge them. We can merge state A and state C. Then the minimized DFA will be

Direct Method for Conversion of RE to FA

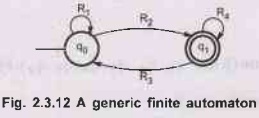
1. State Elimination Method

This is the simplest method of obtaining regular expression. We will use following rules to obtain r.e. by eliminating states

1. Eliminate all the states except final state and start state.

2. Reduce the given finite automata and obtain the generalised transition graph with (start and end states as follows

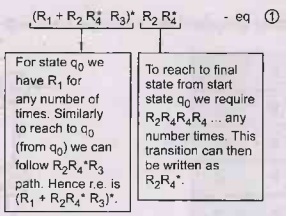
The regular expression for this finite automata will be –

3. If we reduce the finite automaton to only one state graph by state eliminating method then -

4. After eliminating the sufficient number of states we can obtain r.e. as sum of the expressions derived from the reduced automata. Let us understand this method of obtaining regular expression with the help of some examples.

Example 2.3.4 Obtain method r.e. from given FA by state elimination method.

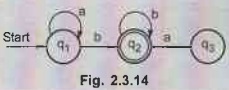
Solution:  In above given FA state q₃ is a dead state. Hence we will eliminate state q₃. Thus the FA now becomes

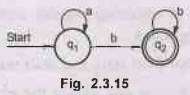
This FA resembles the generic finite automata with two state (as given in Fig. 2.3.15)

Hence required r.e. will be

a*bb* As q₂ is a final state we get

i.e.      r.e. = a*b+

Example 2.3.5 Represent the language given by the following DFA, by obtaining r.e. by state elimination method.

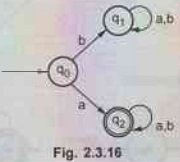
Solution: In above transition graph state q₁ is a dead state. We can not reach to final state from this state, hence we will eliminate state q₁. The FA then becomes as –

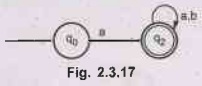
The state q₂ can be written as (a + b) *. Hence the required r.e. is a(a+b)*. This regular expression specifies a language which starts with letter a and it is followed by any number of a's and b's.

Example 2.3.6 Construct Finite automaton to accept the regular expression

(0+1)*(00 + 11)(0+1)*. AU: May-14, Marks 8, May-11, Marks 6

Solution:

The FA for r.e. =(0+1) (00 + 11) (0+1)* as follows –

Example 2.3.7 Construct Finite Automata equivalent to the regular expression (ab +a)*. AU: Dec.-15, Marks 6

Solution: First of all we will construct NFA for given regular expression.

The NFA without ε is

Example 2.3.8 Draw a non-deterministic automata to accept string containing the substring 0101. AU May-16, Marks 2

Solution: The regular expression is

(0+1)* 0101 (0+1)*

The non-deterministric finite automata is

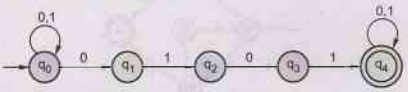
Example 2.3.9 Construct a finite automata for the regular expression 10 + (0+11)0*1  AU Dec.-19, Marks 6

Solution :

Review Question

1. Let r be a regular expression. Then prove that there exists a NFA with & transition that accept L(r).

AU: Dec.-03, Marks 16; Dec.-06, Marks 8; Dec.-10, Marks 10; May-12, Marks 6