Equivalence of NFA and DFA

Equivalence of NFA and DFA

AU: May-05,12,13,14,16,18, Dec.-04,06,14,15,16,19, Marks 13

NFA can be converted to equivalent DFA. Following theorem illustrates this concept.

Theorem: Let L be a set accepted by non-deterministic finite automation. Then there exists a deterministic finite automation that accepts L.

OR

Prove that "A language L is accepted by some DFA if and only if L is accepted by some NFA". AU: Dec.-15, Marks 10, AU: May-05, Dec.-14, Marks 10

Proof :Let

M = (Q, Σ, δ, q₀, F) be an NFA for language L. Then define DFA M' such that,

M' = (Q', Σ`, δ', q<sub>0</sub>`, F')

The states of M' are all the subset of M'. The Q'=2^Q.

F' be the set of all the final states in M.

The elements in Q' will be denoted by [q₁, q₂, q₃, ... q_i] and the elements in Q are denoted by {q₀, q₁, q₂, … }The [q₁, q₂, ... q_i] will be assumed as one state in Q' if in the NFA q₀ is a initial state it is denoted in DFA as q₀` = [q₀]. We define,

δ' ([q₁, q₂, q₃, … q_i], a) = [P₁, P₂, P₃, ... P_j]

if and only if,

8({q₁, q₂ ,q₃, ....q_i}, a) = {P₁, P₂, P₃, …. P_j}

This means that whenever in NFA, at the current states (q₁, q₂, q₃, ...q_i} if we get input a and it goes to the next states [P₁, P₂, ... P_j} then while constructing DFA for it the current state is assumed to be [q₁, q₂, q₃, … q_i, a]. At this state, the input is a and the next is assumed to be [P₁, P₂, ... P_j]. On applying δ function on each of the states q₁, q₂, q₃, ...q_i the new states may be any of the states from [P₁, P₂, ... P_j]. The theorem can be proved with the induction method by assuming length of input string x

δ' (q₀, x) = [q₁, q₂, ... q_i].

if and only if,

δ (q₀, x) = {q₁, q₂, q₃, ... q_i}

Basis: If length of input string is 0

i.e. |x| = 0, that means x is ε then q₀` = [q₀]

Induction: If we assume that the hypothesis is true for the input string of length m or less than m. Then if x a is a string of length m+1. Then the function δ' could be written as,

δ' (q₀, xa) = δ' (δ' (q₀, x), a)

δ' (q₀, x) = [P₁, P₂, … P_j]

if and only if,

δ (q₀, x) = {P₁, P₂, P₃, ... P_j}

By definition of δ'

δ' ([P₁, P₂, … P_j], a) = [r₁, r₂, .... r_k]

if and only if,

δ ({P₁, P₂, … P_j} a) = {r₁, r₂, ... r_k}

Thus

δ' (q₀, x a) = [r₁, r₂, .... r_k]

if and only if

δ (q₀, x a) = {r₁, r₂, ... r_k}

is shown by inductive hypothesis.

Thus L (M) = L (M')

With the help of this theorem, let us try to solve few examples.

Conversion from NFA to DFA

We will discuss the method of converting NFA to its equivalent DFA.

Let, M = (Q, Σ, δ, q₀, F) is a NFA which accepts the language L(M). There should be equivalent DFA denoted by M' = (Q', Σ`, δ', q<sub>0</sub>`, F') such that L(M) = L(M').

The conversion method will follow following steps -

1) The start state of NFA M will be the start for DFA M'. Hence add q₀ of NFA (start state) to Q'. Then find the transitions from this start state.

2) For each state [q₁, q₂, q₃, ... q_i] in Q' the transitions for each input symbol Σ can be obtained as,

i) δ' ([q₁,q₂ ...q_i], a) = δ (q₁, a) U δ (q₂, a) U .........(q_i, a)

= [q₁, q₂, …. q_k ] may be some state.

ii) Add the state [q₁, q₂, .... q_k] to DFA if it is not already added in Q'.

iii) Then find the transitions for every input symbol from Σ for state [q₁, q₂, ....,q_k ]. If we get some state [q₁, q₂, ... q_n ] which is not in Q' of DFA then add this state to Q`.

iv) If there is no new state generating then stop the process after finding all the transitions.

3) For the state [q₁, q₂, …. q_n] ϵ Q' of DFA if any one state q_i is a final state of NFA then [q₁, q₂,......q_n ] becomes a final state. Thus the set of all the final states ϵ F' of DFA.

Example 1.10.1 Determine the DFA from a given NFA.

M = ((q₀, q₁), (a, b), δ, q₀, {q₁}) with the state table diagram for δ given below.

AU Dec.-16, Marks 10, May-18, Marks 13

Solution: Let the DFA M'= (Q', Σ, δ ', q₀, F')

Now, the δ' function will be computed as follows -

As δ (q₀, 0) = {q₀, q₁} δ` ([q₀], 0) = [q₀, q₁]

As in NFA the initial state is q₀, the DFA will also contain the initial state [q₀].

Let us draw the transition table for δ function for a given NFA.

From the transition table we can compute that there are [q₀], [q₁], [q₀, q₁] states for its equivalent DFA. We need to compute the transition from state [q₀, q₁].

δ ({q₀, q₁},0) = δ (q₀, 0) U δ (q₁, 0)

= {q₀, q₁} U ϕ

= {q₀, q₁}

So, δ' ([q₀, q₁], 0) = [q₀, q₁]

Similarly,

δ' ({q₀, q₁}, 1) = δ (q₀,1) U δ (q₁,1)

= {q₁} U {q₀, q₁}

= {q₀, q₁}

So, δ' ([q₀, q₁], 1) = [q₀, q₁]

As in the given NFA q₁ is a final state, then in DFA wherever q₁ exists that state becomes a final state. Hence in the DFA final states are [q₁] and [q₀, q₁]. Therefore set of final states F = {[q₁], [q₀, q₁]}

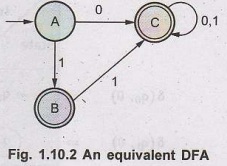
We can even change the names of the states of DFA.

A = [q₀]

B = [q₁]

C= [q₀, q₁]

With these new names the DFA will be as in Fig. 1.10.2.

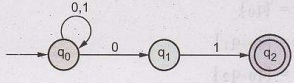
Example 1.10.2 Construct DFA equivalent to the NFA

M = ((p, q, r), (0, 1), δ, p {q, s}) Where & is defined in the following table.

AU: Dec.-04, Marks 8

Solution: To construct DFA,

δ {p, 0} = {q, s} new state generated

δ {p, 1} = {q}

δ {q, 0} = {r}

δ {q, 1} = {q, r} new state

δ {r, 0} = {s}

δ (r, 1) = {p}

δ (s, 0} = -

δ {s, 1} = {p}

δ {{q, s}, 0} = {r}

δ {{q, s}, 1} = {p, q, r} new state

8 {{q, r), 0} = {r, s} new state

δ {{q, r}, 1} = {p, q, r}

δ {{p, q, r}, 0} = {q, r, s} new state

δ {{p, q, r}, 1} = {p, q, r}

δ {{r, s), 0} = {s}

δ {{r, s), 1} = {p}

δ {{q, r, s}), 0} = {r, s}

δ {{q, r, s), 1} = {p, q, r}

The transition table is as shown below.

Example 1.10.3 Construct DFA equivalent to the given NFA.

AU: Dec.-06, Marks 8, Dec.-19, Marks 13

Solution: The NFA M = {{p, q, r, s}, {0, 1}, δ (p), {s}}

The equivalent DFA will be constructed.

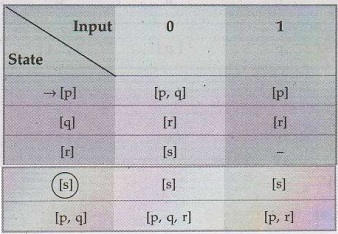
Continuing with the generated new states.

The final state F' = { [s], [p, q, r, s], [p, q, s], [p, r, s], [p, s] }

The transition graph shows two disconnected parts. But part I will be accepted as final DFA because it consists of start state and final states, in part II there is no start state. Refer Fig. 1.10.3 (See Fig. 1.10.3 on next page):

Example 1.10.4 Convert the following NFA to a DFA  . AU: May-13, Marks 10

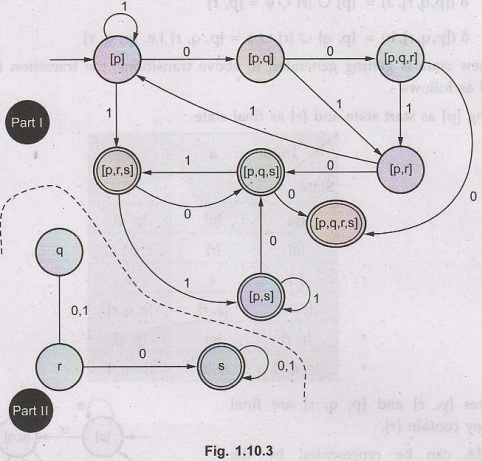
Solution: We will apply δ transitions on each state for each input.

δ ([p], a) = [p]

δ ([p], b) = {p, q} = [p, q] → new state

δ ([q], a) = [r]

δ ([q], b) = [r]

δ ([r], a) = ϕ

δ ([r], b) = ϕ

The 8 transition on newly generated states

δ ([p, q], a) = {p, r} = [p, r] → new state

δ ([p, q], b) = {p, q, r) = [p, q, r] → new state

δ ([p, r], a) = {p} U ϕ = [p]

δ ([p, r], b) = {p, q} U i.e. [p, q]

δ ([p, q, r], a) = {p} U {r} U ϕ = [p, r]

δ ([p, q, r], b) = {p, q} U {r} U ϕ = {p, q, r} i.e. [p, q, r]

As no new state is getting generated in above transitions, the transition table can be constructed as follows -

Assuming [p] as start state and [r] as final state

The states [p, r] and [p, q, r] are final states as they contain [r].

The DFA can be represented by the transition diagarm as shown -

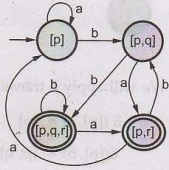
The states [q] and [r] are eliminated as they are dead states.

Example 1.10.5 Construct a DFA accepting binary strings such that the third symbol from the right end is 1. AU May-12, Marks 10

Solution: The strings in such a language are -

The NFA will be,

The transition table can be –

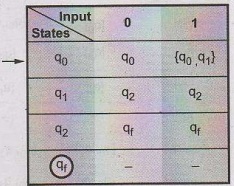
We will obtain the δ transitions on each input and state.

δ (q₀, 0) = [q₀]

δ (q₀, 1) = [q₀, q₁]   i.e. [q₀, q₁] → New state

δ (q₁, 0) = [q₂],      δ (q₁, 1) = [q₂]

δ (q₂, 0) = [q_f],      δ (q₂, 1) = [q_f]

δ ([q₀, q₁], 0) = {q₀, q₂}, = [q₀, q₂] i.e. New state

δ ([q₀, q₁], 1) = {q₀, q₁, q₂} = [q₀, q₁, q₂] → New state

δ ([q₀, q₂], 0) = {q₀, q_F} = {q₀, q_f} → New state

δ ([q₀, q₂], 1) = {q₀, q₁, 9_f} = [q₀, q₁, q_f] → New state

δ ([q₀, q₁, q₂], 0) = {q₀, q₂, q_f} → New state

δ ([q₀, q₁, q₂], 1) = {q₀, q₁, q₂, q_f } → New state

δ ([q₀, q_f], 0) = [q₀]

δ ([q₀, q_f], 1) = [q₀, q₁]

δ ([q₀, q₁, q_f], 0) = [q₀, q₂]

δ ([q₀, q₁, q_f], 1) = [q₀, q₁, q₂]

δ ([q₀, q₂, q_f], 0) =  [q₀, q_f]

δ ([q₀, q₂, q_f], 1) = [q₀, q₁, q_f]

δ ([q₀, q₁, q₂, q_f], 0) = [q₀, q₂, q_f]

δ ([q₀, q₁, q₂, q_f], 1) = [q₀, q₁, q₂, 9_f]

The transition table for above computation is as given below -

The states q₁, q₂ and q_f are not reachable states. Hence they can be eliminated.

Example 1.10.6 Construct a non-deterministic finite automaton accepting the set of strings over {a,b} ending in aba. Use it to construct a DFA accepting the same set of strings.     AU: May-14, Marks 10

Solution: NFA for accepting the strings ending with aba is,

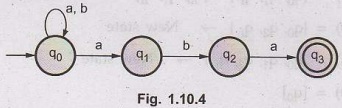
The transition table will be

We will obtain 8 transitions for each input on each state.

δ (q₀, a) = {q₀, q₁} = [q₀, q₁] new state.

 δ (q₀, b) = {q₀}

δ (q₁, a) = ϕ

δ (q₁, b) = {q₂}

δ (q₂, a) = {q₃}

δ (q₂, b) = ϕ

δ (q₃, a) = ϕ

δ (q₃, b) = ϕ

The δ transitions on newly generated states is

δ ([q₀, q₁], a) = {q₀, q₁} i.e. [q₀, q₁]

δ ([q₀, q₁], b) = {q₀, q₂} = [q₀, q₂] new state

δ ([q₀, q₂], a) = {q₀, q₁, q₃} = [q₀, q₁, q₃] new state

δ ([q₀, q₂], b) = {q₀}

δ ([q₀, q₁, q₃], a) = [q₀, q₁]

δ ([q₀, q₁, q₃], b) = [q₀, q₂]

As no new state is getting generated. We will build transition table is as follows -

The DFA will be as shown in Fig. 1.10.5

The states q₁, q₂ and q₃ are non-reachable. Hence they will be eliminated.

Example 1.10.7 Construct a DFA equivalent to the NFA. M=({a, b, c, d}, {0,1} δ, a {b, d}) where δ is a defined as     AU Dec.-14, Marks 6

Solution: Refer similar example 1.10.2 by assuming p = a, q=b, r = c and s = d.

Example 1.10.8 Construct NFA that accepts all string that end in 01. Give its transition table and extended transition function for the input string 00101. Also construct a DFA for the above NFA using subset construction method. AU May-16, Marks 10

Solution: The NFA will be designed using

r.e. = (0+1)* 01

The transition table will be as follows:

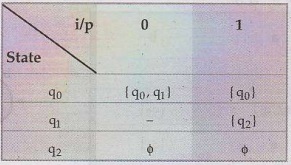
Refer example 1.10.6 for conversion of NFA to DFA.

Review Question

1. Prove that "A language L is accepted by some DFA if and only if L is accepted by some NFA".      AU Dec.-15, Marks 10