Deterministic Finite Automata (DFA)

Deterministic Finite Automata (DFA)

AU: Dec.-07, 10, 11, 13, 16, 19, May-07, 14, Marks 13

The finite automata is called Deterministic Finite Automata if there is only one path for a specific input from current state to next state. For example, the DFA can be shown in Fig. 1.6.1.

From state S₀ for input 'a' there is only one path, going to S₂. Similarly from S₀ there is only one path for input b going to S₁.

The DFA can be represented by the same 5-tuples described in the definition of FSM.

Definition of DFA

A deterministic finite automation is a collection of following things -

1) The finite set of states which can be denoted by Q.

2) The finite set of input symbols Σ.

3) The start state q₀ such that q₀ ϵ Q.

4) A set of final states F such that F ϵ Q.

5) The mapping function or transition function denoted by δ. Two parameters are passed to this transition function: One is current state and other is input symbol. The transition function returns a state which can be called as next state.

For example, q₁ = δ (q₀, a) means from current state q₀, with input a the next state transition is q₁.

In short, the DFA is a five tuple notation denoted as :

A = (Q, Σ, δ, q₀, F)

The name of DFA is A which is a collection of above described five elements.

Example 1.6.1 Design a FA which checks whether the given binary number is even.

Solution:  

• Logic: The binary number is made up of 0's and 1's when any binary number ends with 0 it is always even and when a binary number ends with 1 it is always odd. For example,

0100 is a even number, it is equal to 4.

0011 is a odd number, it is equal to 3.

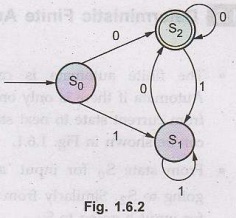
• Design: While designing FA we will assume one start state one state ending in 0 and other state for ending with 1. Since we want to check whether given binary number is even or not, we will make the state for 0, as the final state. (Refer Fig. 1.6.2)

Simulation: The FA indicates clearly S₁ is a state which handles all the 1's and S₂ is a state which handles all the 0's. Let us take some input.

01000 => 0S₂1000

01S₁ 000

010S₂ 00

0100S₂ 0

01000S₂

Another idea to represent FA with the help of transition table.

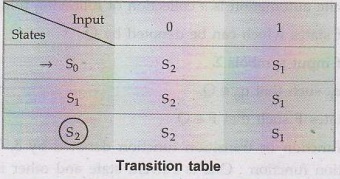
Example 1.6.2 Design FA which checks whether the given unary number is divisible by 3.

Solution:

• Logic :

The unary number is made up of ones. The number 3 can be written in unary form as 111, number 5 can be written as 11111 and so on.

The unary number which is divisible by 3 can be 111 or 111111 or 111111111 and so on.

• Design

• Simulation

Consider a number 111111 which is equal to 6 i.e. divisible by 3. So after complete scan of this number we reach to final state q₃.

Start 111111

State q0

1q₁ 11111

11q₂ 1111

111q₃ 111

1111q₁ 11

11111q₂ 1

111111q₃ → Now we are in final state.

Example 1.6.3 Design FA to check whether given decimal number is divisible by three.

Solution:

• Logic :

To determine whether the given decimal number is divisible by three, we need to take the input number digit by digit.

Also, while considering its divisibility by three, we have to consider that the possible remainders could be 1, 2 or 0. The remainder 0 means, it is divisible by 3. Hence from input set {0, 1, 2, …. 9} (since decimal number is a input), we will get either remainder 0 or 1 or 2 while testing its divisibility by 3. So we need to group these digits according to their remainders.

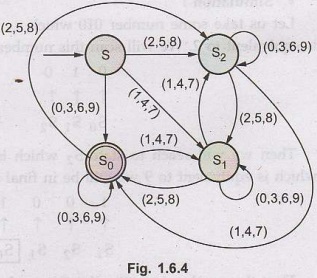
The groups are as given below -

remainder 0 group: S₀: (0, 3, 6, 9)

remainder 1 group: S₁: (1, 4, 7)

remainder 2 group: S₂: (2,5,8)

We have named out these states as S₀, S₁ and S₂. The state So will be the final state as it is remainder 0 state.

• Design:

• Simulation:

Let us test the above FA, if the number is 36 then it will proceed by reading the number digit by digit.

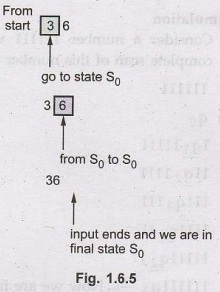
Hence the number is divisible 3, isn't it ? Similarly if number is 121 which is not divisible by 3, it will be processed as

S 121

1 S₁ 21

12 S₀ 1

121 S₁         which is remainder 1 state.

Example 1.6.4 Design FA which checks whether a given binary number is divisible by three.

Solution:

• Logic:

We will consider the input digit by digit.

While considering the divisibility by 3, we should think of three types of states, namely-

remainder 0 i.e. S₀ state

remainder 1 i.e. S₁ state

remainder 2 i.e. S₂ state

• Design:

• Simulation:

Let us take some number 010 which is equivalent to 2. We will scan this number from MSB to LSB.

0    1    0

↑    ↑    ↑

S₀  S₁  S₂

Then we will reach to state S₂ which is remainder 2 state. Similarly for input 1001 which is equivalent to 9 we will be in final state after scanning the complete input.

1   0   0   1

↑   ↑   ↑   ↑

S₁ S₂ S₁ S₀

Thus the number is really divisible by 3.

We can also represent the simulation in following manner -

Consider input 1001

S Ⱶ 001

1 Ⱶ S₁ 001

10 Ⱶ S₂ 01

100 Ⱶ S₁ 1

1001 Ⱶ S₀   i.e. ACCEPT state

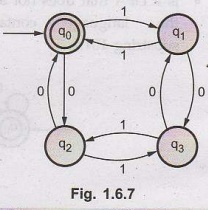
Example 1.6.5 Consider the finite automata transition table shown below with F = {q₀}    AU: Dec.-10, Marks 10

Find the language accepted by the finite automata.

Solution: The transition diagram for the given transition table will be as shown in Fig. 1.6.7.

• The sets accepted by this language are (0011, 00, 11, 1010, 0101, ... }

• This shows that all the strings contain even number of 0's and even number of 1's. Hence the language accepted by this finite automata contains "all the strings having even number of O's and even number of 1's".

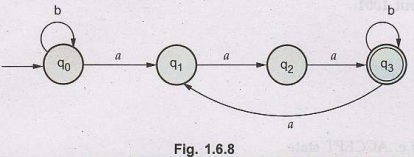
Example 1.6.6 Design FA to accept L, where L = {Strings in which a always appears trippled) over the set Σ = {a, b}.   AU: Dec.-10, Marks 10

Solution:

• Logic: For this particular language the valid strings are aaab, baaaaaa, bbaaab and so on. The a always appears in a clump of 3.

Note that in Fig. 1.6.8 the sequence of tripple a is maintained to reach to the final state.

• Design

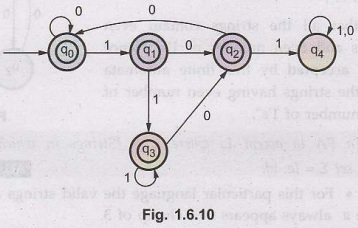
Example 1.6.7 Construct a DFA that accepts all the strings on {0, 1} except those containing the substring 101.

AU: May-07, Marks 6, May-14, Marks 8

Solution :

• The simplest method to construct such DFA is to construct DFA for the language containing the substring 101.

• Now just change the non-final states to final states and make final state as non-final state. The DFA then becomes shown in Fig. 1.6.9.

• is a DFA that does not accept the language containing substring 101.

Example 1.6.8 Define DFA. Design a DFA to accept the binary numbers which are divisible by 5.

Solution: i) DFA - Refer section 1.6.

ii) DFA for divisibility by 5: For designing DFA as a divisibility by 5 tester for a binary string we will consider following states.

q₀ - remainder 0 state

q₁ - remainder 1 state

q₂ - remainder 2 state

q₃ - remainder 3 state

q₄ - remainder 4 state

Now we will design DFA by considering above states and finding next states with input 0 and 1.

The DFA will be

Simulation: Consider the string (1111)₂ = (15)₁₀

q₀ Ⱶ 1111

1q₁ Ⱶ 111

11q₃ Ⱶ 11

111q₂ Ⱶ 1

1111q₀ Ⱶ

Divisible by 5.         q₀ is a final state.

Consider input string (1110) = (14) 10

q0 Ⱶ 1110

1 q₁ Ⱶ 110

11 q₃ Ⱶ 10

111 q₂ Ⱶ 0

1110 q₄ Ⱶ

Remainder 4.      q₄ is remainder 4 state.

Example 1.6.9 Draw transition diagram for recognizing the set of all operators in C language. AU: Dec.-07, Marks 10

Solution:

• Logic: In C language there are various operators, such as relational operators bitwise operators and arithmetic operators. Various relational operators are <,  <=, >=, !=, ==. The bitwise operators are &&, ||. Let us draw the transition diagram for these operators.

• Design:

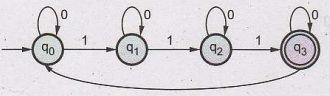
Example 1.6.10 Construct a DFA accepting all string w over {0, 1}, such that number of 1's in w is 3 mod 4.  AU: Dec.-11, Marks 8

Solution: The DFA will be

Example 1.6.11 Give deterministic finite automata accepting the following language over the alphabet.

1) Number of 1's is a multiple of 3.

2) Number of 1's is not a multiple of 3.  AU: Dec.-13, Marks 8

Solution: 1) We assume alphabet as input set Σ = {1}

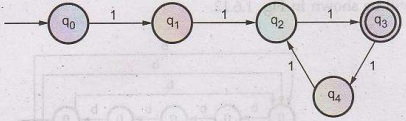
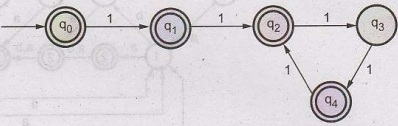
2) For recognizing number of 1's not a multiple of 3, we will use the DFA in step (1). That means we will make non final states as final and final state as non-final ones. The DFA will then be as shown in figure.

Example 1.6.12 Given Σ = (a, b), construct a DFA which recognize the language

L= {b^m abⁿ :m,n>0}.  AU Dec.-16, Marks 6

Solution:

• The m and n are > 0 and there is no restriction on number of m and n. In other words any number of m and n are allowed except null.

• Hence we can rewrite given L as

L = b⁺ ab⁺

• From this L we can construct DFA as

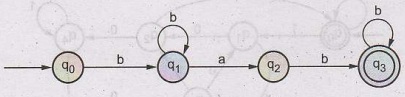
Example 1.6.13 Construct a DFA to accept strings over (a, b), such that every block of length five contains at least two a's. Use extended transition of function to trace a string W = aabba.

Solution: The following DFA contains block of five symbols. The DFA loops back when the block ends. At each state both the a and b symbols are considered. The state names indicate the total number of a's so far visited. For instance if the state name is 1 then it indicates that there is single a being read. When two a's are read then it leads to a final state. The DFA will be shown in Fig. 1.6.12.

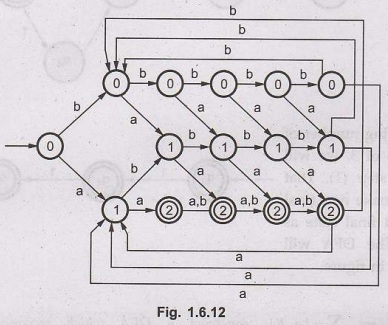
Example 1.6.14 Design a DFA which accept strings of O's and 1's which when interpreted as a binary integer is multiple of 5. Also give the sequence of states that DFA is in while processing the input string: 1001011.

Solution: The required DFA can be drawn as follows.

Processing of 1001011

q₀ Ⱶ 1001011

1 q₁ Ⱶ 001011

10 q₂ Ⱶ 01011

100 q₄ Ⱶ 1011

1001 q₄ Ⱶ 011

10010 q₃ Ⱶ 11

100101 q₂ Ⱶ 1

1001011 q₀ Ⱶ Accept.

Example 1.6.15 Design a FA for following language

L = {W|W is Binary word of length 4i (where i >= 1) such that each consecutive block of 4 bits contains atleast 2 0s} = {0000, 0110, 01101100, ...)  AU: Dec 19, Marks 13

Solution :