Describing Variability

Describing Variability

• Variability, almost by definition, is the extent to which data points in a statistical distribution or data set diverge, vary from the average value, as well as the extent to which these data points differ from each other. Variability refers to the divergence of data from its mean value and is commonly used in the statistical and financial sectors.

• The goal for variability is to obtain a measure of how spread out the scores are in a distribution. A measure of variability usually accompanies a measure of central tendency as basic descriptive statistics for a set of scores.

• Central tendency describes the central point of the distribution and variability describes how the scores are scattered around that central point. Together, central tendency and variability are the two primary values that are used to describe a distribution of scores.

• Variability serves both as a descriptive measure and as an important component of most inferential statistics. As a descriptive statistic, variability measures the degree to which the scores are spread out or clustered together in a distribution.

• Variability can be measured with the range, the interquartile range and the standard deviation/variance. In each case, variability is determined by measuring distance.

Range

• The range is the total distance covered by the distribution, from the highest score to the lowest score (using the upper and lower real limits of the range).

Range=Maximum value - Minimum value

Merits :

a) It is easier to compute.

b) It can be used as a measure of variability where precision is not required. Demerits :

a) Its value depends on only two scores

b) It is not sensitive to total condition of the distribution.

Variance

• Variance is the expected value of the squared deviation of a random variable from its mean. In short, it is the measurement of the distance of a set of random numbers from their collective average value. Variance is used in statistics as a way of better understanding a data set's distribution.

• Variance is calculated by finding the square of the standard deviation of a variable.

σ²= Σ(Χ - μ)² /N

• In the formula above, μ represents the mean of the data points, x is the value of an individual data point and N is the total number of data points.

• Data scientists often use variance to better understand the distribution of a data set. Machine learning uses variance calculations to make generalizations about a data set, aiding in a neural network's understanding of data distribution. Variance is often used in conjunction with probability distributions.

Standard Deviation

• Standard deviation is simply the square root of the variance. Standard deviation measures the standard distance between a score and the mean.

Standard deviation=√Variance

• The standard deviation is a measure of how the values in data differ from one another or how spread out data is. There are two types of variance and standard deviation in terms of sample and population.

• The standard deviation measures how far apart the data points in observations are from each. we can calculate it by subtracting each data point from the mean value and then finding the squared mean of the differenced values; this is called Variance. The square root of the variance gives us the standard deviation.

• Properties of the Standard Deviation :

a) If a constant is added to every score in a distribution, the standard deviation will not be changed.

b) The center of the distribution (the mean) changes, but the standard deviation remains the same.

c) If each score is multiplied by a constant, the standard deviation will be multiplied by the same constant.

d) Multiplying by a constant will multiply the distance between scores and because the standard deviation is a measure of distance, it will also be multiplied.

• If user are given numerical values for the mean and the standard deviation, we should be able to construct a visual image (or a sketch) of the distribution of scores. As a general rule, about 70% of the scores will be within one standard deviation of the mean and about 95% of the scores will be within a distance of two standard deviations of the mean.

• The mean is a measure of position, but the standard deviation is a measure of distance (on either side of the mean of the distribution).

• Standard deviation distances always originate from the mean and are expressed as positive deviations above the mean or negative deviations below the mean.

• Sum of Square (SS) for population definition formula is given below:

          Sum of Square (SS) = Σ(x-μ)²

• Sum of Square (SS) for population computation formula is given below:

           SS= ΣΧ²- (ΣΧ)²/ N

• Sum of Squares for sample definition formula:

          SS = Σ (X-X̄)²

• Sum of Squares for sample computation formula :

          SS = Σx² - (Σx)²/n

Example 2.8.1: The heights of animals are: 600 mm, 470 mm, 170 mm, 430 mm and 300 mm. Find out the mean, the variance and the standard deviation.

Solution:

Mean = 600+ 470 + 170+ 430 + 300 / 5

=1970 /5= 394

σ²= Σ(Χ - μ)²/ N

Variance = (600-394)² + (470-394)² + (170-394)² + (430-394)² + (300-394)² /5

Variance = 42436+5776+ 50176 + 1296 +8836 / 5

Variance = 21704

Standard deviation = √Variance = √21704

= 142.32 ≈ 142

Example 2.8.2: Using the computation formula for the sum of squares, calculate the population standard deviation for the scores: 1, 3, 7, 2, 0, 4, 7, 3.

Solution: Calculate mean of data

Mean = 1+3+7+2+0+4+7+3 / 8 = 3.375

Variance = (3.375-1)² + (3.375-3)² + (3.375-7)² + (3.375-2)² + (3.375-0)² + (3.375−4)² + (3.375 − 7)² + (3.375 – 3)² /8

= (-2.375)² + (0.375)² + (3.625)² + (−1.375)² + (-3.375)² + (0.625)² + (3.625)² + (−0.375)² /8

= 5.64+0.14+13.14+1.89+11.39+0.39+13.14+0.14 /8

= 45.87 /8 = 5.73

Variance = 5.73

The population standard deviation is the square root of the variance = (5.73)^1/2 = 2.393

The Interquartile Range

• The interquartile range is the distance covered by the middle 50% of the distribution (the difference between Q1 and Q3).

• Fig. 2.8.1 shows IQR.

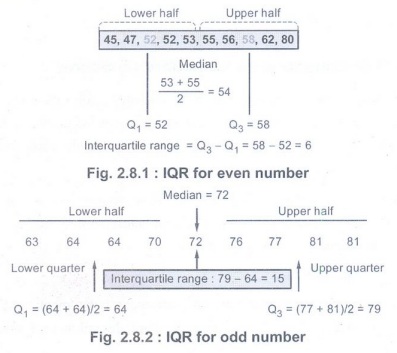
• The first quartile, denoted Q1, is the value in the data set that holds 25% of the values below it. The third quartile, denoted Q3, is the value in the data set that holds 25% of the values above it.

Example 2.8.3: Determine the values of the range and the IQR for the following sets of data.

(a) Retirement ages: 60, 63, 45, 63, 65, 70, 55, 63, 60, 65, 63

(b) Residence changes: 1, 3, 4, 1, 0, 2, 5, 8, 0, 2, 3, 4, 7, 11, 0, 2, 3, 4

Solution:

a) Retirement ages: 60, 63, 45, 63, 65, 70, 55, 63, 60, 65, 63

Range = Max number - Min number = 70-45

Range = 25

IQR:

Step 1: Arrange given number form lowest to highest.

 45, 55, 60, 60, 63, 63, 63, 63, 65, 65, 70

                                ↑  

                           Median

Q1=60 , Q3 65

IQR = Q3-Q1=65-60 = 5