Decoders

Decoders      AU :Dec-06,08,11,12,18,May-07,09,11,15,19

• A decoder is a multiple-input, multiple-output logic circuit which converts coded inputs into coded outputs, where the input and output codes are different.

• The Fig. 1.15.1 shows the general structure of the decoder circuit.

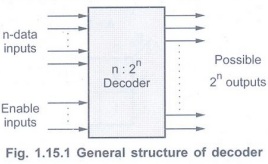
• The encoded information is presented as n inputs producing possible outputs.

• The 2ⁿ output values are from 0 through 2ⁿ - 1.

• Usually, a decoder is provided with enable inputs to activate decoded output based on data inputs. When any one enable input is unasserted, all outputs of decoder are disabled.

Binary Decoder

• A decoder which has an n-bit binary input code and a one activated output out of 2ⁿ output code is called binary decoder.

• A binary decoder is used when it is necessary to activate exactly one of 2ⁿ outputs based on an n-bit input value.

• Fig. 1.15.2 shows 2-to-4 decoder.

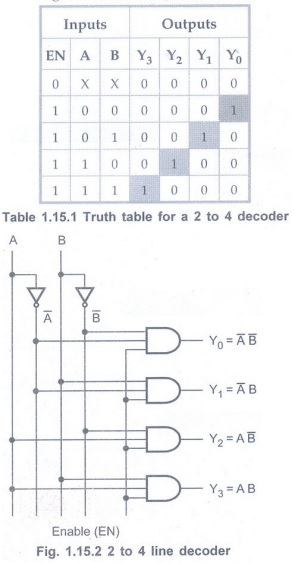
• 2 inputs are decoded into four outputs, each output representing one of the minterms of the 2 input variables.

• The two inverters provide the complement of the inputs, and each one of four AND gates generates one of the minterms.

• The Table 1.15.1 shows the truth table for a 2-to-4 decoder.

• If enable input is 1 (EN = 1), one, and only one, of the outputs Y₀ to Y₃, is active for a given input.

• The output Y₀ is active, i.e. Y₀ = 1 when inputs A = B = 0, the output Y₁ is active when inputs A = 0 and B = 1.

• If enable input is 0, i.e. EN =0, then all the outputs are 0.

Example 1.15.1 Draw the circuit for 3 to 8 decoder and explain.

Solution :Fig. 1.15.3 shows 3-to-8 line decoder. Here, 3 inputs are decoded into eight outputs, each output represent one of the minterms of the 3 input variables. The three inverters provide the complement of the inputs, and each one of the eight AND gates generates one of the minterms. Enable input is provided to activate decoded output based on data inputs A, B, and C. The table shows the truth table for 3-to-8 decoder.

Expanding Cascading Decoders

• Binary decoder circuits can be connected together to form a larger decoder circuit.

• Fig. 1.15.4 shows the 4 x 16 decoder using two 3 x 8 decoders.

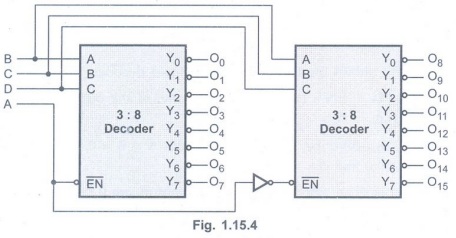
• Here, one input line (D) is used to enable/disable the decoders.

• When D = 0, the top decoder is enabled and the other is disabled. Thus the bottom decoder outputs are all 1s, and the top eight outputs generate minterms 0 0 0 0 to 0 1 1 1.

• When D=1, the enable conditions are reversed and thus bottom decoder outputs generate minterms 1000 to 1111, while the outputs of the top decoder are all 1s. 

Example 1.15.2 Design 5-to-32 decoder using one 2-to-4 and four 3-to-8 decoder ICs.  AU Dec.-11, May-15, Marks 16

Solution: The Fig. 1.15.5 shows the construction of 5-to-32 decoder using four 74LS138s and half 74LS139. The half section of 74LS139 IC is used as a 2-to-4 decoder to decode the two higher order inputs, D and E. The four outputs of this decoder are used to enable one of the four 3 to 8 decoders. The three lower order inputs A, B and C are connected in parallel to four 3 to 8 decoders. This means that the same output pin of each of the four 3-to-8 decoders is selected but only one is enabled. The remaining enable signals of four 3-to-8 decoder ICs are connected in parallel to construct enable signals for 5-to-32 decoder.

(See Fig. 1.15.5 on next page.)

Realization of Boolean Function using Decoder

• The combination of decoder and external logic gates can be used to implement single or multiple output functions.

• When decoder output is active high, it generates minterms (product terms) for input variables; i.e. it makes selected output logic 1. In such case to implement SOP function we have to take sum of selected product terms generated by decoder.

Examples for Understanding

Example 1.15.3 Implement Boolean function F = ∑ m (1, 2, 3, 7) using 3 : 8 decoder.

Solution :

Step 1: Connect function variables as inputs to the decoder.

Step 2: Logically OR the outputs correspond to present minterms to obtain the output.

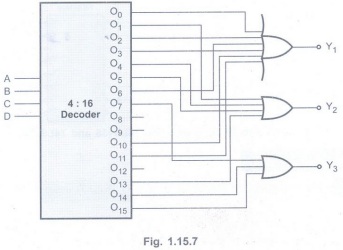
Example 1.15.4 Implement the following multiple output combinational logic using a 4 line to 16 line decoder.

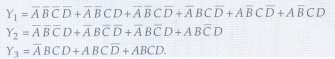
Solution:

Step 1:Write the function in their minterm forms

Y₁ = ∑ m (0, 3, 2, 6, 10, 11) Y₂ =∑ m (1, 4, 5, 13) Y₃ =∑m (7, 14, 15)

Step 2: Logically OR the outputs of decoder corresponding to the minterms in the functions.

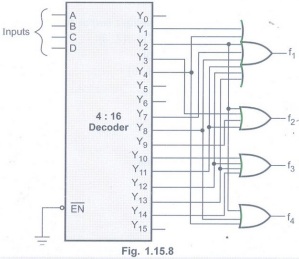
Example 1.15.5 Implement the following multiple output combinational logic circuit using a 4-line to 16-line decoder.

f₁ = ∑m (1, 2, 4, 7, 8, 11, 12, 13), f₂ = ∑m (2, 3, 9, 11)

f₃ =∑m (10, 12, 13, 14), f₄ = ∑m (2, 4, 8)  AU: Dec.-08, Marks 10

Solution :

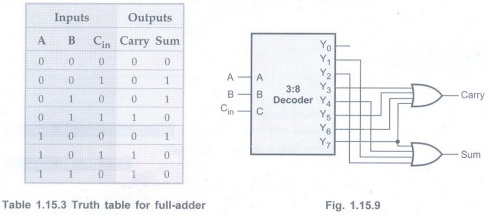
Example 1.15.6 Design and implement a full adder circuit using a 3: 8 decoder. AU May-11, Marks 5

Solution : Truth table for full adder is as shown in the Table 1.15.3.

Examples for Practice

Example 1.15.7

Design an excess-3 to BCD code converter using decoder and gates.

Example 1.15.8

Design 2×4 decoder using NAND gates.

Example 1.15.9

Design a combinational logic circuit defined by the functions

F1 = a'b'c'd + a'c'd' + ab'cd', F2 = a'b'c + b'cde' + a'bcde'

F3 = abcd' + ab'cd' + abcde'

Example 1.15.10 Implement the following multiple output function using suitable decoder.

f₁ (A, B, C)= ∑ m(0, 4, 7)+d(2, 3)

f₂ (A, B, C) = ∑ m(1, 5, 6)

f₃ (A, B, C)= ∑ m(0, 2, 4, 6)

Applications of Decoders

The uses of decoders are :

• Code converters

• Implementaion of combinatonal circuits

• Address decoding

• BCD to 7-segment decoder

Decoder ICs

Review Questions

1. Define decoder.

2. Define binary decoder.

3. Explain the working of 2: 4 binary decoder.

4. Draw a 4 x 16 decoder constructed with two 3 x 8 decoders.  AU: May-07, Dec.-12, Marks 2

5. State the procedure to implement Boolean function using decoder.

6. Mention the uses of decoders.  AU Dec.-06, Marks 2

7. What is decoder? Draw the block diagram and truth table for 2 to 4 decoder.  AU May-09, 19, Marks 2

8. Explain in detail about decoders.  AU: Dec.-18, Marks 6