Constraint Satisfaction

UNIT I

Chapter: 6: Constraint Satisfaction Problems (CSP)

Constraint Satisfaction

Constraint Satisfaction Problems - The Concept

1. Constraint satisfaction problem has various states and goal test, a tranditional problem has been converted into standard structured and very simple "representation".

2. The general-purpose routines can be used to access a special representation which has more benefit than problem-specific heuristics. These routines combined with special structure can find solution of large problems.

3. The structure of the problem is represented in different form such as, standard representation of the goal test.

4. The revealed structured is very efficient in many ways such as,

i) Problem decomposition.

ii) To understand structure of problem and the diffculty of solving it and their connection.

5. If the problem is treated as CSP we have many advantages, as discussed below.

i) As the representation of states have standard pattern [that is a set of variables with assigned values], we can design successor function and goal test in generic way that will apply to all CSPs.

ii) We can develop effective generic heuristic that require no additional domain specific expertise.

iii) The structure of the constraint graph can be used to simplify the solution process in some cases giving exponential reduction in complexity.

Formal Definition of Constraint Satisfaction Problems

1. A constraint satisfaction problem is defined by a set of variables X₁, X₂,...., X_n and a set of constraints C₁, C₂, ..., C_m.

2. Each variable X₁ has a nonempty domain D₁ of possible values.

3. Each constraint C1 involves some subset of the variables and specifies the allowable combinations of values for that subset.

4. A state of the problem is defined by an assignment of values to some or all of the variables {X_i = V_i, X_j = V_j,.... }

5. An assignment that does not violate any constraints is called a consistent or legal assignment.

6. A complete assignment is one in which every variable is mantained and a solution to a CSP is, a complete assignment that satisfies all the constraints.

7. Some CSPs also require a solution that maximizes an objective function.

Consider following graph colouring problem.

Constraints are -

1) We have three colours for colouring avertex.

2) No two adjacent vertices have same colour. Given three colours-(Red, Green, Blue). Allowable combination for A, B vertices would be,

{(R, G), (R, B), (G, R), (G, B), (B, R), (B, G)}

Examples of CSP

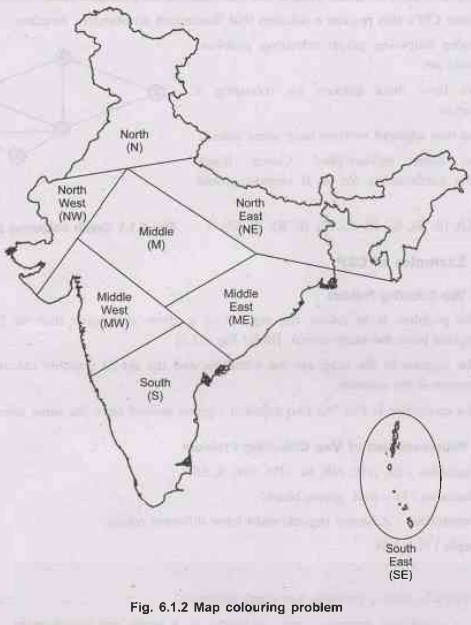
1. Map Colouring Problem

1. The problem is to colour the regions of a given map such that no 2 adjacent regions have the same colour. [Refer Fig. 6.1.2]

2. The regions in the map are the variables and the set of possible colours for the regions is the domain.

3. The constraint is that "no two adjacent regions should have the same colour."

Formal Representation of Map Colouring Problem

1. Variables: (N, NW, NE, M, MW, ME, S, SE}

2. Domains: D = (red, green, blue}

3. Constraints: Adjacent regions must have different colors.

Example: N ≠ NW

Note

1. Typically, such a problem has many solutions.

2. We sometimes represent map colouring as a graph coloring (constraint graph) problem.

3. The topology of a constraint graph can sometimes be used to identify solutions easily.

Example Map

2. Other Examples of CSP

1. N-queens puzzle.

2. Jobshop scheduling.

3. Scene labelling.

4. Circuit board layout.

5. Map colouring problem.

6. Sudoku

7. Boolean satisfiability.

Some real-world problems

1. Assignment problems.

2. Transporation scheduling.

3. Hardware configuration.

4. Spreadsheets.

5. Factory scheduling.

6. Floor planning.

Incremental Formulation for CSP

• It is fairly easy to see that a CSP can be given an incremental formulation as a standard serach problem as follows:

i) Initial state -

The empty assignment {}, in which all variables are unassigned.

ii) Successor functions -

A value can be assigned to any unassigned variable, provided that it does not conflict with previously assigned variables.

iii) Goal test -

The current assignment is complete.

iv) Path cost -

A constant cost for every step.

Searching for Goal State in CSP

1. Every solution must be a complete assignment and therefore appears at depth n if there are n variables.

2. The search tree extends only to depth n.

3. Depth-first search algorithms are popular for CSPs.

4. The path by which a solution is reached is irrelevant.

5. We can also use a complete-state formulation, in which every state is a complete assignment that might or might not satisfy the constraints.

6. Local search methods work well for this formulation.

Variations in CSPs

1. The simplest kind of CSP involves variables that are discrete and have finite domains. Graph-coloring problems are of this kind. The 8-queens problem described can also be viewed as finite-domain CSP, where the variables Q1,..., Q8 are the positions of each queen in colums 1,..., 8 and each variable has the domain (1, 2, 3, 4, 5, 6, 7, 8). If the maximum domain size of any variable is a CSP in d, then the number of possible complete assignments are O(dⁿ) that is exponential in the number of variables.

2. Finite-domain CSPs include Boolean CSPs, whose variables can be either true or false. Boolean CSPs include, as special cases, some NP-complete problems, such as 3SAT.

3. In most practical applications, however, general-purpose CSP algorithms can solve problems of orders of magnitude larger than those solvable via the general-purpose search algorithms that we saw.

4. Discrete variables can also have infinite domains-for example, the set of integers or the set of strings.

5. Constraints satisfaction problems with continuous domains are very common in the real world and are widely studied in the field of operations research.

For example, the scheduling of experiments on the Hubble Space Telescope requires very precise timing of observations; the start and finish of each observation and maneuver are continuous-valued variables that must obey a variety of astronomical, precedence and power constraints. The best-known category of continuous-domain CSPs is that of linear programming problems where constraints must be linear inequalities.

Constraints in CSPs

1. Properties of Constraints

Constraints are used to guide reasoning of everyday common sense. The constraints have following properties.

1. Constraints may specify partial infomation; constraint need not uniquely specify the values of its variables.

2. Constraints are non-directional, typically a constraint on (say) two variables V₁, V₂ can be used to infer a constraint on V₁ given a constraint on V₂ and viceversa.

3. Constraints are declarative; they specify what relationship must hold without specifying a computational procedure to enforce that relationhip.

4. Constraints are additive; the order of imposition of constraints does not matter, all that matters at the end is that the conjunction of constraints is in effect.

5. Constraints are really independent; typically constraints in the constraint store (i.e. collection of constraints) share variables.

2. Types of Constraints in CSPs

1. Unary constraint - Which restricts the value of a single variable. Every unary be eliminated simply by prepressing the domain of the corresponding variable to remove any value that violates the constraint.

For example- Constraint can be that, Vertex A can not be coloured with bluecolour.

2. Binary constraint - Relates two variables. A binary CSP is one with only binary constraints; it can be represented as a constraint graph.

For example - In graph colouring problem two adjacent vertices can not have same colour.

3. Higher-order constraints -

Involves three or more variables. A familiar example is provided by cryptarithmetic puzzles. It insist that each letter in a cryptarithmetic puzzle represent a different digit. Higher-order constraints can be represented in a constraint hypergraph. Such as shown below:-

Example 1 -

The cryptarithmatic problem. (A CSP problem having high order constraints)

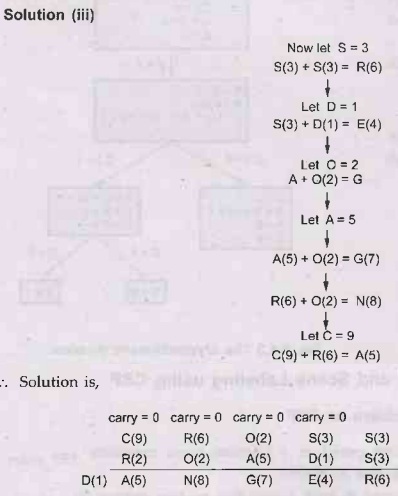
Example 2 - Explain the constraint satisfaction procedure to solve the cryptarithmetic problem.

Solution: (At each step minimum possible value is selected.)

General Algorithm for Finding Solution in CSP

1. Propagate available constraints -

i) Open all objects that must be assigned values in a complete solution.

ii) Repeat until inconsistency or all objects are assigned valid values: Select an object and strengthen as much as possible, the set of constraints that apply to object. If set of constraints are different from previous set, then open all objects that share any of these constraints. Remove selected object.

2. If union of constraints discovered above defines a solution then return solution.

3. If union of constraints discovered above defines a contradiction then return failure.

4. Make a guess in order to proceed. Repeat until a solution is found or all possible solutions exhausted;

i) Select an object with a no assigned value and try to strengthen its constraints.

ii) Recursively invoke constraint satisfaction with the current set of constraints plus the selected strengthening constraint.

• CSP Representation as a Constraint Graph

The CSP can be represented in terms of the constraint graph. A constrain graph has,

1. Nodes as variables (For example In graph-colouring problem the vertex is variable which needs to be coloured. This vertex will be a node in constraint graph.)

2. Arcs as a constraints (For example - In graph-colouring problem the arc will denote that no two adjacent vertices will have same colour.)

• Advantages of Constraint Graph

1. The organization of constraint graph is very much useful for simplification of CSP's solutions.

2. It reduces complexity in exponential manner.