Discrete Mathematics: Unit III: Graphs
Connectivity
Graphs - Discrete Mathematics
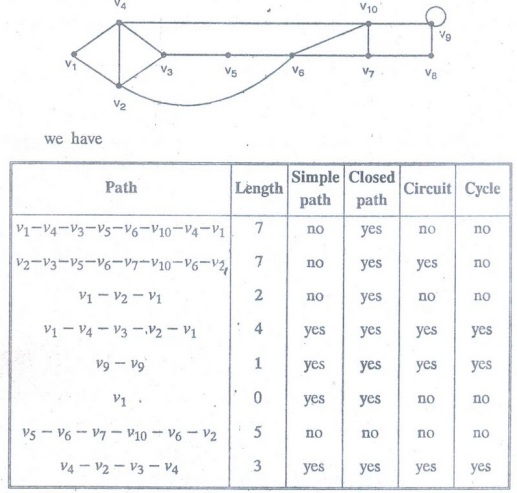
A path in a multigraph G consists of an alternating sequence of vertices and edges of the form V0, e1 V1, e2, V2, … en-1, Vn-1, en, Vn
CONNECTIVITY
Definition:
Path
A
path in a multigraph G consists of an alternating sequence of vertices and
edges of the form
V0,
e1 V1, e2, V2, … en-1, Vn-1,
en, Vn
where
each edge ei contains the vertices Vi-1 and Vi
The
number n of edges is called the length of the path.
The
path is said to be closed if Vo = Vn we say the path is
from Vo to Vn or between Vo and Vn or
Connects Vo to Vn.
Note :
1.
A simple path is a path in which all vertices are distinct. (A path in which
all edges are district will be called a trail)
2.
If Vo = Vn, then P is called a closed path. On the other
hand if Vo ≠ Vn, then P is an open path.
3.
For the following graph

Definition:
Circuit:
A
path of length ≥ 1 with no repeated edges and whose end vertices are same is
called a circuit.
Note
:
4.
A cycle is a circuit with no other repeated vertices except its end vertices.
5.
A cycle is a simple circuit, a loop is a cycle of length 1.
6.
In a graph a cycle that is not a loop must have length atleast 3, but there may
be cycles of length 2 in a multigraph.
7.
Two paths in a graph are said to be edge-disjoint if they have no common edges,
they are vertex - disjoint if they have no common vertices.
Definition:
Path graph
A
path graph of order 'n' is obtained by removing on edge from a Cn
graph, denoted by Pn.
Definition:
Trail
A
trail from v to w is a path from v to w that does not contain a repeated edge.
Thus
a trial from v to w is a path of the form
v
= v0, e1, v1, e2, ... vk-1,
ek, vk = w where all the ei are distinct.
Note:
Every simple path is also a trail, and every trail is also a path, but these
inclusion do not reverse.
Example 1: Does each of these lists
of vertices from a path in the following graph? Which paths are simple? Which
are circuits? What are the lengths of those that are paths?
(a) a, e, b, c, b (b) e, b, a, d, b, e
(c) a, e, a, d, b, c, a (d) c, b, d, a, e, c
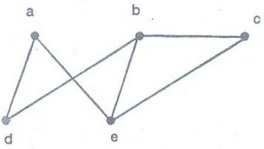
Solution :
(a)
path of length 4, not a circuit, not simple.
(b)
not a path
(c)
not a path
(d)
simple circuit of length 5.
Definition:
Connected and disconnected graphs
A
graph G is a connected graph is there is atleast one path between every pair of
vertices in G. Otherwise G is a disconnected graph.
Example:
Note:
A disconnected graph consists of two or more connected graphs. Eachof these
connected subgroups is called a component (or a block).
Example 2. Determine whether the
given graph is connected.
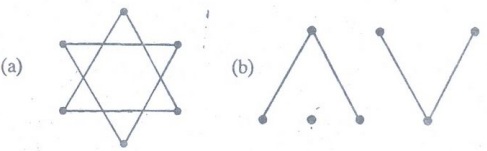
Solution:
(a) No (b) No
Example 3. For the following graph
Theorem:
If a graph G (either connected or not) has exactly two vertices of odd degree,
there is a path joining these two vertices.
Proof:
Case (i) Let G be connected.
Let
v1 and v2 be the only vertices of G with are of odd
degree.
But
we know that number of odd vertices is even.
Clearly
there is a path connecting v1 and v2, because G is
connected.
Case
(ii) Let G be disconnected.
Then
the components of G are connected.
Hence
v1 and v2 should belong to the same component of G.
Hence,
there is a path between v1 and v2.
Theorem :
The
maximum number of edges in a simple disconnected graph G with n vertices and k
components is (n - k) (n - k + 1)
Proof :
Let
the number of vertices in the ith component of G be n1 (ni
≥1)

Now
the maximum number of edges in the ith component of
G
= ½ ni (ni − 1)
Therefore
maximum number of edges of G
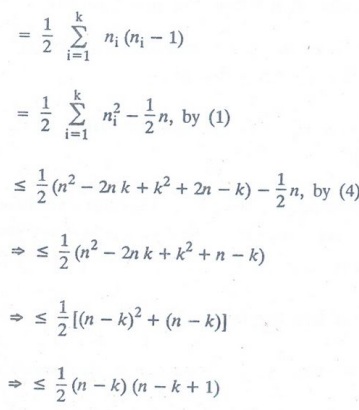
Example 3. Let G = (V,E) be a
simple graph. Let R be the relation on V consisting of pairs of vertices (u, v)
such that there is a path from u to v or such that u = v. Show that R is an
equivalence relation.
Solution :
(i) Reflextive :
R
is reflexive by definition.
(ii) Symmetry:
Assume that (u, v) ϵ R, then there is a path from u to v. Then (v, u) ϵ R
because there is a path from v to u.
(iii) Transitive:
Assume
that (u, v) ϵ R and (v, w) ϵ R; then there are paths from u to v and from v to
w. Putting these two paths together gives a path from u to w.
Hence,
(u, w) ϵ R. It follows that R is transitive.
Theorem:
There is a simple path between every pair of distinct vertices of a connected
undirected graph.
Proof:
Let u and v be two distinct vertices of the connected undirected graph G = (V, E).
Since
G is connected, there is at least one path between u and v. Let x0,
x1,...,xn, where x0 = u and xn = v,
be the vertex sequence of a path of least length.
This
path of least length is simple.
Suppose
it is not simple. Then xi = xj for some i and j with 0 ≤ i
< j.
This
means that there is a path from u to v of shorter length with vertex sequence x0,
x1, ..., xi-1, xj, ..., xn obtained
by deleting the edges corresponding to the vertex sequence xi, ..., xi-1.
Example 4. What are the connected
components of the graph H shown in figure.
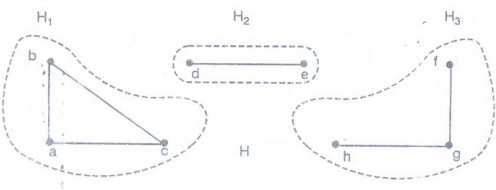
Solution:
The graph H is the union of three disjoint connected subgraphs H1, H2,
and H3.
These
three subgraphs are the connected components of H.
Definition:
A directed graph is strongly connected if there is a path from a to b and from
b to a whenever a and b are vertices in the graph.
Definition:
A directed graph is weakly connected if there is a path between every two
vertices in the underlying undirected graph.
Example 5. Are the directed graphs
G and H shown in figure strongly connected? Are they weakly connected?
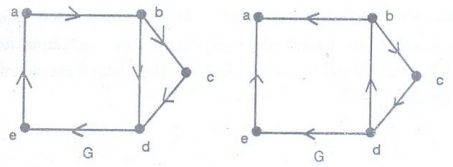
Solution:
G is strongly connected because there is a path between any two vertices in
this directed graph. Hence, G is also weakly connected.
The
graph H is not strongly connected. There is no directed path from a to b
in this graph. However, H is weakly connected, because there is a path between
any two vertices in the underlying undirected graph of H.
Cut vertex, Cut set
and Brige
A
cut vertex of a connected graph G is a vertex whose removal increases the
number of components. Clearly if v is a cut vertex of a connected graph G, G - v
is disconnected. A cut vertex is also called a cut point.
Bridge:
If
a graph G is connected and e is an edge such that G - e is not connected, then e is said to be a bridge or a cut edge.
Paths in Acquaintanceship Graphs:
In an acquaintanceship graph there is a path between two people if there is a
chain of people linking these people, where two people adjacent in the chain
know one another.
Paths in Collaboration Graphs:
In a collaboration graph two vertices a and b, which represent authors, are
connected by a path when there is a sequence of authors beginning at a and
ending at b such that the two authors represented by the endpoints of each edge
have written a joint paper.
Paths in the Hollywood graph:
In the Holly wood graph two vertices a and b are linked when there is a chain
of actors linking a and b, where every two actors adjacent in the chain have
acted in the same movie.
Example 6. Find all the cut
vertices of the given graph.
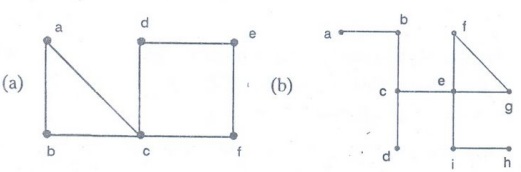
Solution :
(a)
e
(b) b, c, e, i
Example 7. Suppose that v is an
endpoint of a cut edge. Prove that v is a cut vertex if and only if this vertex
is not pendant.
Solution:
If a vertex is pendant it is clearly not a cut vertex. A endpoint of a cut edge
that is a cut vertex is not pendant.
Remove
of a cut edge produces a graph with more connected components than in the
original graph.
If
an endpoint of a cut edge is not pendant, the connected component it is in
after the remove cut edge contains more than just this vertex.
From
this, removal of that vertex and all edges incident to it, including the
original cut edge, produces a graph with more connected components than were in
the original graph.
Hence,
an endpoint of a cut edge that is not pendant is a cut vertex.
Theorem:
Let G be a graph with adjacency matrix A with respect to the ordering 1, 2,
..., n (with directed or undirected edges, with multiple edges and loops
allowed). The number of different paths of length r from i to j, where r is a positive integer, equals the (i,j)th entry of Ar.
Example 8. Show that a simple graph
G with n vertices is connected if it has more than (n - 1) (n - 2)/2 edges.
Solution:
Suppose
that G is not connected.
Then
it has a component of k vertices for some k, 1 ≤ k ≤ n-1.
The
most edges G could have is
C
(k, 2) + C (n-k, 2) = [k (k-1) + (n - k) (n - k-1)]/2
=
k2 - nk + (n2 - n)/2.
This
quadratic function off is minimized at k = n/2 and maximized at k = 1 or k = n-1.
Hence,
if G is not connected, then the number of edges does not exceed the value of
this function at 1 and at n-1, namely, (n - 1) (n - 2)/2.
Example 9. How many paths of length
four are there from a to d in the simple graph G in figure. [A.U N/D 2012]
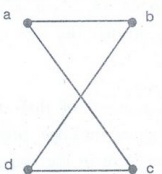
Solution:
The adjacency matrix of G (ordering the vertices as a, b, c, d) is

Hence,
the number of paths of length four from a
to d is the (1, 4)th entry of A4.
Since

there
are exactly eight paths of length four from a
to d. From this graph, we see that a,
b, a, b, d; a, b, a, c, d; a, b, d, b, d; a, b, d, c, d ; a, c, a, b, d; a, c,
a, c, d; a, c, d, b, d; and a, c, d, c, d are the eight paths from a to d.
EXERCISES
3.4
1.
Determine whether each of these graphs is strongly connected and if not,
whether it is weakly conected.

2.
Find the strongly connected components of each of these graphs.
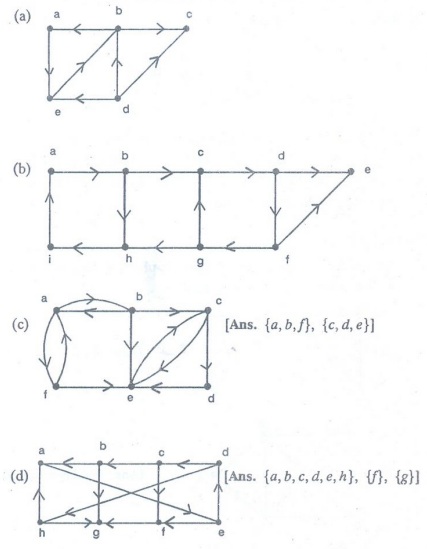
3.
Show that all vertices visited in a directed path connecting two vertices in
the same strongly connected component of a directed graph are also in this
strongly connected component.
4.
Find the number of paths of length n between two different vertices in K4
if n is
(a) 2
[Ans. 2]
(b)
3 [Ans. 7]
(c)
4 [Ans. 20]
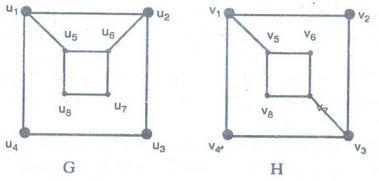
5.
Use paths either to show that these graphs are not isomorphic or to find an isomorphism
between these graphs.
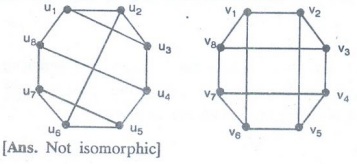
6.
Use paths either to show that these graphs are not isomorphic or to find an
isomorphism between them.
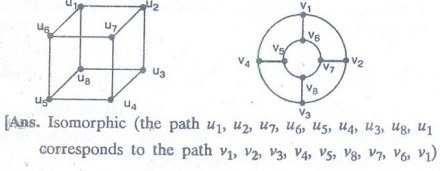
7.
Use paths either to show that these graphs are not isomorphic or to find an
isomorphism between them.
8.
Show that every connected graph with n vertices has at least n-1 edges.
9.
Show that in every simple graph there is a path from any vertex of odd degree
to some other vertex of odd degree.
10.
Show that a vertex c in the connected
simple graph G is a cut vertex if and only if there are vertices u and v, both different from c, such that every path between u and v passes through c.
11.
Show that a simple graph with at least two vertices has at least two vertices
has at least two vertices that are not cut vertices.
12.
Show that an edge in a simple graph is a cut edge if and only if this edge is
not part of any simple circuit in the graph.
13.
Show that if a connected simple graph G is the union of the graph G1
and G2, then G1 and G2 have at least one
common vertex.
14.
Show that if a simple graph G has k
connected components and these components have n1, n2,
..., nk vertices, respectively, then the number of edges of G does
not exceed
Σki=1
C (ni, 2)
15.
How many nonisomorphic connected simple graphs are there with n vertices when n is
(a)
2?[Ans. 1] (b) 3? [Ans. 2] (c) 4? [Ans. 6] (d)
5? [Ans. 21]
16.
Let P1 and P2 be two simple paths between the vertices u and in the simple graph G that do not
contain the same set of edges. Show that there is a simple circuit in G.
17.
Show that a simple graph G is bipartite if and only if it has no circuits with
an odd number od edges.
18.
Explain why in the collaboration graph of mathematicians a vertex representing
a mathematician is in the same connected component as the vertex representing
Paul Erdos if and only if that mathematician has a finite Erdos number.
Discrete Mathematics: Unit III: Graphs : Tag: : Graphs - Discrete Mathematics - Connectivity
Related Topics
Related Subjects
Discrete Mathematics
MA3354 3rd Semester CSE Dept | 2021 Regulation | 3rd Semester CSE Dept 2021 Regulation
