Combining Multiple Learners

Combining Multiple Learners

• When designing a learning machine, we generally make some choices like parameters of machine, training data, representation, etc. This implies some sort of variance in performance. For example, in a classification setting, we can use a parametric classifier or in a multilayer perceptron, we should also decide on the number of hidden units.

• Each learning algorithm dictates a certain model that comes with a set of assumptions. This inductive bias leads to error if the assumptions do not hold for the data.

• Different learning algorithms have different accuracies. The no free lunch theorem asserts that no single learning algorithm always achieves the best performance in any domain. They can be combined to attain higher accuracy.

• Data fusion is the process of fusing multiple records representing the same real-world object into a single, consistent, and clean representation. Fusion of data for improving prediction accuracy and reliability is an important problem in machine learning.

• Combining different models is done to improve the performance of deep learning models. Building a new model by combination requires less time, data, and computational resources. The most common method to combine models is by a weighted average improves the averaging multiple models, where taking a weighted average improves the accuracy.

1. Generating Diverse Learners:

• Different Algorithms: We can use different learning algorithms to train different base-learners. Different algorithms make different assumptions about the data and lead to different classifiers.

• Different Hyper-parameters: We can use the same learning algorithm but use it with different hyper-parameters.

• Different Input Representations: Different representations make different characteristics explicit allowing better identification.

• Different Training Sets: Another possibility is to train different base-learners by different subsets of the training set.

Model Combination Schemes

• Different methods are used for generating final output for multiple base learners are Multiexpert and multistage combination.

1. Multiexpert combination.

• Multiexpert combination methods have base-learners that work in parallel.

a) Global approach (learner fusion): given an input, all base-learners generate an output and all these outputs are used, such as voting and stacking and to

b) Local approach (learner selection): in mixture of experts, there is a gating model, which looks at the input and chooses one (or very few) of the learners as responsible for generating the output.

• Multistage combination: Multistage combination methods use a serial approach where the next multistage combination base-learner is trained with or tested on only the instances where the previous base-learners are not accurate enough.

• Let's assume that we want to construct a function that maps inputs to outputs from a set of known N_train input-output pairs.

• Let's assume that we want to construct a function that maps inputs to outputs from a set of known N_train input-output pairs.

D _train = {(x, y)}_i=1^Ntrain

where x_i Є X is a D dimensional feature input vector, y_i Є Y is the output.

• Classification: When the output takes values in a discrete set of class labels Y = {C₁; C₂;... C_x), where K is the number of different classes. Regression consists in predicting continuous ordered outputs, Y = R.

Voting

• The simplest way to combine multiple classifiers is by voting, which corresponds to taking a linear combination of the learners. Voting is an ensemble machine learning algorithm.

• For regression, a voting ensemble involves making a prediction that is the average of multiple other regression models.

• In classification, a hard voting ensemble involves summing the votes for crisp class labels from other models and predicting the class with the most votes. A soft voting ensemble involves summing the predicted probabilities for class labels and predicting the class label with the largest sum probability.

• Fig. 9.1.1 shows Base-learners with their outputs.

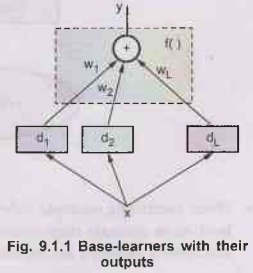
• In this methods, the first step is to create multiple classification/regression models using some training dataset. Each base model can be created using different splits of the same training dataset and same algorithm, or using the same dataset with different algorithms, or any other method.

• Learn multiple alternative definitions of a concept using different training data or different learning algorithms. It combines decisions of multiple definitions, e.g. box using weighted voting.

Fig. 9.1.2 shows general idea of Base-learners with model combiner.

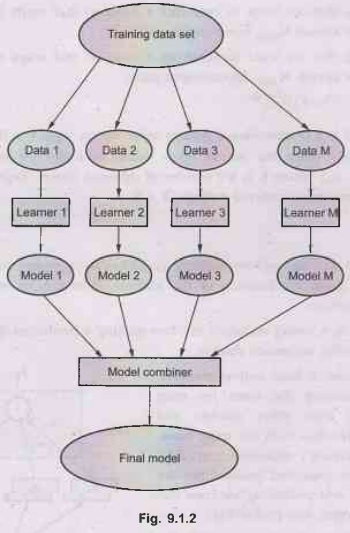
• When combining multiple independent and diverse decisions each of which is at least more accurate than random guessing, random errors cancel each other out, and correct decisions are reinforced. Human ensembles are demonstrably better.

• Use a single, arbitrary learning algorithm but manipulate training data to make it learn multiple models.

Error-Correcting Output Codes

• In Error-Correcting Output Codes main classification task is defined in terms of a number of subtasks that are implemented by the base-learners. The idea is that the original task of separating one class from all other classes may be a difficult problem.

• So, we want to define a set of simpler classification problems, each specializing in one aspect of the task, and combining these simpler classifiers, we get the final classifier.

• Base-learners are binary classifiers having output - 1/ +1, and there is a code matrix W of K × L whose K rows are the binary codes of classes in terms of the L base-learners d_j.

• Code matrix W codes classes in terms of learners

• One per class L = K

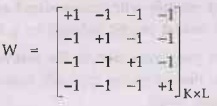
• The problem here is that if there is an error with one of the base-learners, there may be a misclassification because the class code words are so similar. So the approach in error-correcting codes is to have L > K and increase the Hamming distance between the code words.

• One possibility is pairwise separation of classes where there is a separate base-learner to separate C_i from C_j, for i < j.

• Pairwise L = K(K − 1)/2

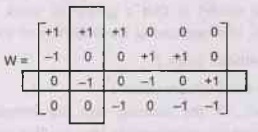
• Full code L = 2^(K-1) – 1

• With reasonable L, find W such that the Hamming distance between rows and between columns are maximized.

• Voting scheme are

y_i = Σ^t_j=1 W_ijd_j

and then we choose the class with the highest Y_i.

• One problem with ECOC is that because the code matrix W is set a priori, there is Porno guarantee that the subtasks as defined by the columns of W will be simple.