Code Conversion

Code Conversion

AU May-04, 05, 06, 07, 08, 10, 12, 13, 14, 19, Dec.-03,05, 08,09,10, 12, 14,15 16

• There are different codes such as Binary-Coded-Decimal (BCD), Excess-3, Gray and so on. Many times it is required to convert one code to another.

• The procedure to design code converters :

Step 1:Write the truth table showing the relationship between input code and output code.

Step 2:For each output code bit determine the simplified Boolean expression using K-map.

Step 3:Realize the code converter using logic gates.

Illustrative Examples

Example 1.13.1 Design a 4-bit binary to BCD converter.

AU: Dec.-08,15, Marks 10

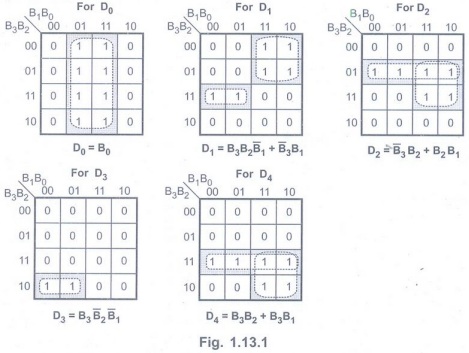
Step 1:Form the truth table relating binary and BCD code.

Input code: Binary code : B₃ B₂ B₁ B₀ (B₀, LSB)

Output code: BCD (Decimal) code : D₃ D₂ D₁ D₀ (D₀, LSB)

Step 2: K-map simplification for each BCD output

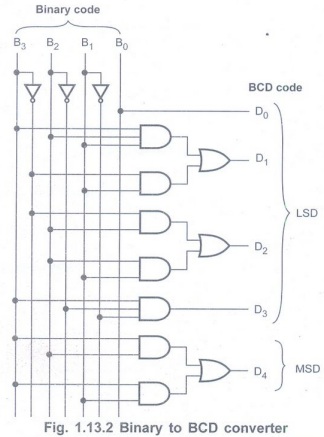
Step 3: Realization of code converter

Example 1.13.2 Design a logic circuit to convert BCD to gray code.

AU May-05, 07, Marks 12

Solution :

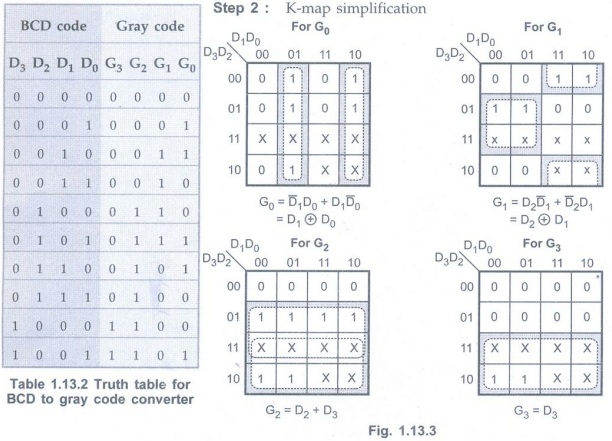
Step 1: Form the truth table relating BCD and gray code.

Input code: BCD code : D₃ D₂ D₁ D₀ (D₀, LSB)

Output code: Gray code: G₃ G₂ G₁ G₀ (D₀,LSB)

Step 2:K-map simplification

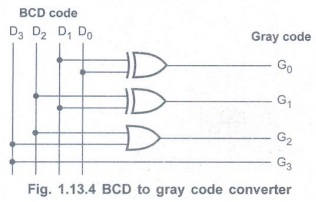
Step 3: Realization of code converter

Example 1.13.3 Design a logic circuit to convert the 8421 BCD to Excess-3 code.

AU May-04, 05, 08, 10, 12, 14, 19, Dec.-03, 10, 12, 16, Marks 12

Solution :

Step 1: Form the truth table relating BCD and Excess-3 code

Excess-3 code is a modified form of a BCD number. The Excess-3 code can be derived from the natural BCD code by adding 3 to each coded number. For example, decimal 12 can be represented in BCD as 0001 0010. Now adding 3 to each digit we get Excess-3 code as 0100 0101 (12 in decimal). With this information the truth table for BCD to Excess-3 code converter can be determined as shown in Table 1.13.3.

Input code: BCD code: D₃ D₂ D₁ D₀ (D₀, LSB)

Output code: Excess-3 code: E₃ E₂ E₁ E₀ (D₀, LSB)

Step 2: K-map simplification for each Excess-3 code output.

Step 3:Realization of code converter.

Example 1.13.4 Design and implement a 8421 to gray code converter. Realize the converter using only NAND gates.  AU: Dec.-05, 14, 16, May-06, 13, Marks 12

Solution :

Step 1: Form the Truth table relating 8421 binary code and Gray code

Input code: Binary code : B₃ B₂ B₁ B₀

Output code:Gray code: G₃ G₂ G₁ G₀

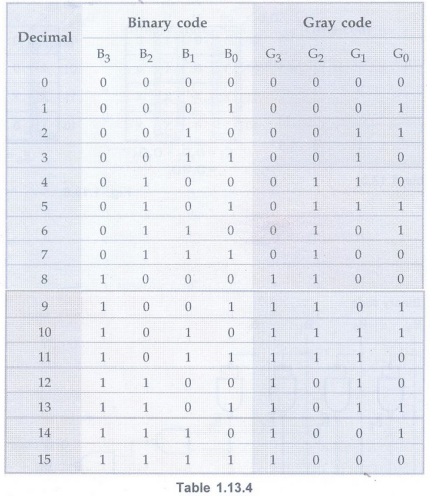
Step 2: K-map simplification for each gray code output

Step 3:Realization of code converter using XOR-gates

Step 4: Realization of code converter using NAND gates

For this converter we have derived the Boolean expressions for each gray code output in the sum of product (SOP) form. We can implement SOP expression using AND-OR logic or NAND-NAND logic. Let us see the implementation of code converter using NAND-NAND logic.

Example 1.13.5 Design a gray to BCD code converter.AU May-08, Marks 12

Solution: The Table 1.13.5 shows truth table for gray to BCD code converter.

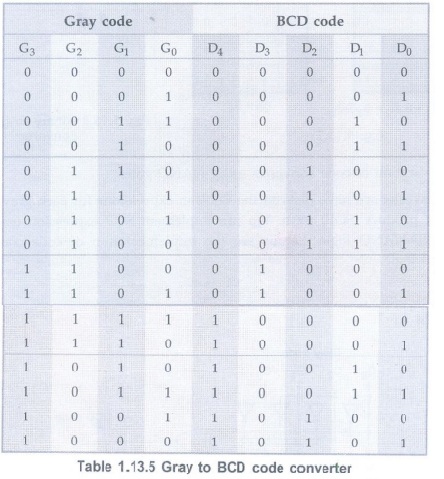
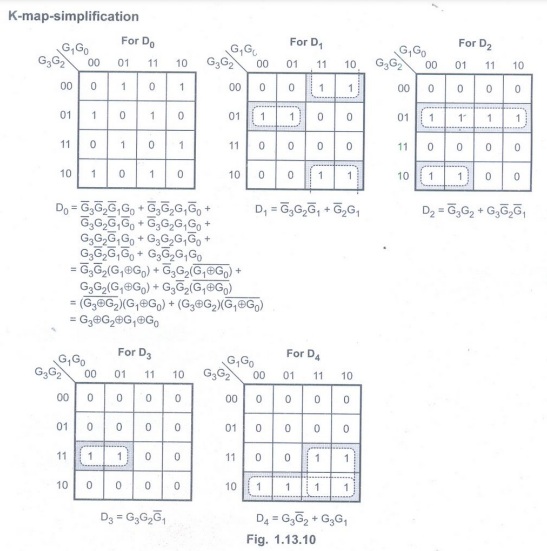
K-map-simplification

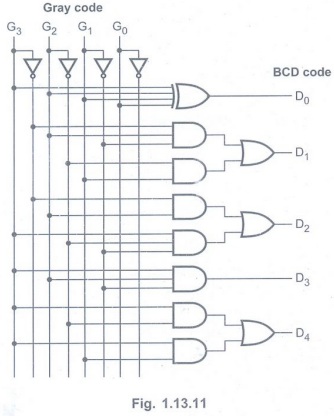
Logic diagram

Examples for Practice