Clustering

Clustering

• Given a set of objects, place them in groups such that the objects in a group are similar (or related) to one another and different from (or unrelated to) the objects in other groups.

• Cluster analysis can be a powerful data-mining tool for any organization that needs to identity discrete groups of customers, sales transactions, or other types of behaviors and things. For example, insurance providers use cluster analysis to detect fraudulent claims and banks used it for credit scoring.

• Cluster analysis uses mathematical models to discover groups of similar customers based on the smallest variations among customers within each group.

• Cluster is a group of objects that belong to the same class. In another words the similar object are grouped in one cluster and dissimilar are grouped in other cluster.

• Clustering is a process of partitioning a set of data in a set of meaningful subclasses. Every data in the sub class shares a common trait. It helps a user understand the natural grouping or structure in a data set.

• Various types of clustering methods are partitioning methods, hierarchical clustering, fuzzy clustering, density based clustering and model based clustering.

• Cluster anlysis is process of grouping a set of data objects into clusters.

• Desirable properties of a clustering algorithm are as follows:

1. Scalability (in terms of both time and space)

2. Ability to deal with different data types

3. Minimal requirements for domain knowledge to determine input parameters.

4. Interpretability and usability.

• Clustering of data is a method by which large sets of data are grouped into clusters of smaller sets of similar data. Clustering can be considered the most important unspervised learning problem.

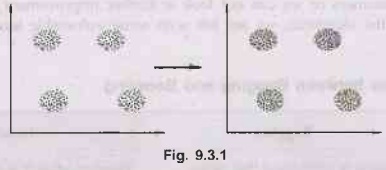
• A cluster is therefore a collection of objects which are "similar" between them and are dissimilar" to the objects belonging to other clusters. Fig. 9.3.1 shows cluster.

• In this case we easily identify the 4 clusters into which the data can be divided; the similarity criterion is distance: two or more objects belong to the same cluster if they are "close" according to a given distance (in this case geometrical distance). This is called distance-based clustering.

• Clustering means grouping of data or dividing a large data set into smaller data sets of some similarity.

• A clustering algorithm attempts to find natural groups components or data based on some similarity. Also, the clustering algorithm finds the centroid of a group of data sets.

• To determine cluster membership, most algorithms evaluate the distance between a point and the cluster centroids. The output from a clustering algorithm is basically a statistical description of the cluster centroids with the number of components in each cluster.

• Cluster centroid: The centroid of a cluster is a point whose parameter values are the mean of the parameter values of all the points in the cluster. Each cluster has a well defined centroid.

• Distance: The distance between two points is taken as a common metric to as see the similarity among the components of population. The commonly used distance measure is the euclidean metric which defines the distance between two points

p= (P₁, P₂,...) and q = (q₁,q₂,...) is given by,

d = Σ ^k_i=1 (p_i - q_i)²

• The goal of clustering is to determine the intrinsic grouping in a set of unlableled data. But how to decide what constitutes a good clustering? It can be shown that there is no absolute "best" criterion which would be independent of the final aim of the clustering. Consequently, it is the user which must supply criterion, in such a way that the result of the clustering will suit their needs.

• Clustering analysis helps construct meaningful partitioning of a large set of objects Cluster analysis has been widely used in numerous applications, including pattern recognition, data analysis, image processing etc.

• Clustering algorithms may be classified as listed below:

1. Exclusive clustering

2. Overlapping clustering

3. Hierarchical clustering

4. Probabilisitic clustering.

• A good clustering method will produce high quality clusters high intra- class similarlity and low inter class similarity. The quality of a clustering result depends on both the similarity measure used by the method and its implementation. The quality of a clustering method is also measured by it's ability to discover some or all of the hidden patterns.

• Clustering techniques types: The major clustering techniques are,

a) Partitioning methods

b) Hierarchical methods

c) Density-based methods.

Unsupervised Learning K-means

• K-Means clustering is heuristic method. Here each cluster is represented by the center of the cluster. "K" stands for number of clusters, it is typically a user input end to the algorithm; some criteria can be used to automatically estimate K.

• This method initially takes the number of components of the population equal to the final required number of clusters. In this step itself the final required number sons of clusters is chosen such that the points are mutually farthest apart.

• Next, it examines each component in the population and assigns it to one of the clusters depending on the minimum distance. The centroid's position is recalculated everytime a component is added to the cluster and this continues until all the components are grouped into the final required number of clusters.

• Given K, the K-means algorithm consists of four steps:

1. Select initial centroids at random.

2. Assign each object to the cluster with the nearest centroid.

3. Compute each centroid as the mean of the objects assigned to it.

4. Repeat previous 2 steps until no change.

The X₁,..., X_N are data points or vectors of observations. Each observation mot (vector x_i) will be assigned to one and only one cluster. The C(i) denotes cluster number for the i^th observation. K-means minimizes within-cluster point scatter:

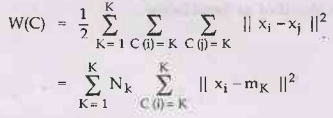
where

m_k is the mean vector of the K^th cluster.

N_K is the number of observations in K^th cluster.

K-Means Algorithm Properties

1. There are always K clusters.

2. There is always at least one item in each cluster.

3. The clusters are non-hierarchical and they do not overlap.

4. Every member of a cluster is closer to its cluster than any other cluster because closeness does not always involve the 'center' of clusters.

The K-Means Algorithm Process

1. The dataset is partitioned into K clusters and the data points are randomly assigned to the clusters resulting in clusters that have roughly the same number of data points.

2. For each data point.

a. Calculate the distance from the data point to each cluster.

b. If the data point is closest to its own cluster, leave it where it is.

c. If the data point is not closest to its own cluster, move it into the closest cluster.

3. Repeat the above step until a complete pass through all the data points results in no data point moving from one cluster to another. At this point the clusters are stable and the clustering process ends.

4. The choice of initial partition can greatly affect the final clusters that result, in terms of inter- cluster and intracluster distances and cohesion.

• K-means algorithm is iterative in nature. It converges, however only a local minimum is obtained. It works only for numerical data. This method easy to implement.

• Advantages of K-Means Algorithm:

1. Efficient in computation

2. Easy to implement.

• Weaknesses

1. Applicable only when mean is defined.

2. Need to specify K, the number of clusters, in advance.

3. Trouble with noisy data and outliers.

4. Not suitable to discover clusters with non-convex shapes.