Boolean Algebra

BOOLEAN ALGEBRA

Def. Boolean Algebra

A Boolean algebra is a complemented, distributive lattice.

Note: 1. George boole in 1854 had given a set of basic rules for logic in his book "The laws of thought". Boolean algebra provides the operations and rules working with the binary set {0, 1}

2. Electronic circuites and switching matchings are working with the rules of Boolean algebra.

Properties

We shall denote the unary operation of complementation by ', so that for any a Є B, the complement of a is denoted by a' Є B.

Most of the properties of a Boolean algebra have been derived in the previous section. We shall list some of the important properties here. It may be mentioned that the properties listed here are not independent of each other.

Example :

Let A = {a, b, c} and consider the lattice P (A).

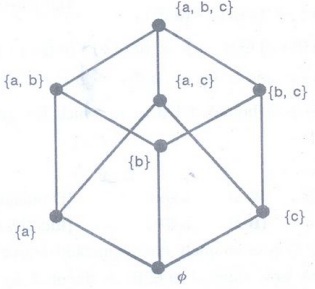
Clearly < P (A), ∩, U > is a Boolean Algebra.

Example 3. Consider the D₃₀ = {1, 2, 3, 5, 6, 10, 15, 30} is a lattice (infact Boolean algebra) with relation "divides".

Solution: Now

2*1 = 1     3*1= 1         5*1= 1

2*2 = 2     3*2 = 1        5*2 = 1

2*3 = 1     3*3 = 3        5*3 = 1

2*5 = 1     3*5 = 3        5*5 = 5

2*6 = 2     3*6 = 3        5*6 = 1

2*10 = 1   3*10 = 1      5*10 = 5

2*15 = 1   3*15 = 3      5*15 = 5

2*30 = 2   3*30 = 3      5*30 = 5

2, 3, 5 are atoms in D₃₀.

Example 4. Show that in any Boolean algebra,

(a + b) (a' + c) = ac + a' b + bc    [MU, Oct. 1996]

Solution: Let (B, +, ., ') be a Boolean algebra, and a, b, c Є B

L.H.S = (a + b) (a' + c) (a + b) a' + (a + b) c

= aa' + ba' + ac + bc

= 0 + a' b + ac + bc

= ac + a' b + bc = R.H.S.

Example 7. Theorem : Prove that every finite Bolean algebra

(B, V, ^, -) has 2ⁿ elts for some positive integer 'n'.

Proof : By theorem, we have

(B, V, A, -) is isomorphic to (P(A), U, ∩, C) where A is the set of all atoms in B.

Suppose that A has 'n' atoms for some positive integers n. Then P(A) has 2ⁿ elts.

Since B = P(A), B has also 2ⁿ elts.

Example 9. Let a, b, c be any elements in a Boolean algebra B. Prove

that (i) a* a = a, (ii) a + a = a

Solution :

(i) To prove a * a = a

Let a = a *1    by identity law.

= a * (a + a')      by complement law.

= a*a + a*a'     by distributive law.

= (a* a) + 0       by complement law.

= a * a        by identity law.

(ii) To prove a + a = a

Let a = a + 0    by identity law.

a = a + (a* a')    by complement law.

= (a + a) * (a + a')    by distributive law.

= (a + a) * 1    by complement law.

= a + a     by identity law.

Example 10. Let a, b, c be any elements in a Boolean algebra B. Show that (i) a + 1 = 1, (ii) a * 0 = 0

Solution:

(i) To prove a + 1 = 1

Let a + 1 = (a + 1) * 1    by identity law.

= (a + 1) * (a + a')       by complement law.

= a + (1 * a')    by distributive law.

= a + (a' * 1)     by commutative law.

= a + a'      by identity law.

= 1     by complement law.

(ii) To prove a * 0 = 0

Let a 0 = (a* 0) + 0     by identity law.

= (a*0) + (a * a')      by complement law.

= a * (0 + a')      by distributive law.

= a * (a' + 0)      by commutative law.

= a * a'       by identity law.

= 0     by complement law.

Example 11. Let a, b, c be any elements in a Boolean algebra B. Show that (i) a + (a * b) = a, (ii) a * (a + b) = a

Solution :

(i) To prove a + (a*b) = a

Let a + a * b = a * 1 + a * b  by identity law.

= a * (1 + b)    by distributive law.

= a * (b + 1)   by commutative law.

= a + 1     by dominance law.

 = a      by identity law.

(i) To prove a * (a + b) = a

Let a * (a + b) = (a + 0) * (a + b)     by identity law.

= a + (0 * b)      by distributive law.

= a + (b * 0)         by commutative law.

= a + 0      by dominance law.

= a       by identity law.

Example 12. Let a, b, c be any elements in a Boolean algebra B show that (i) (a + b) + c = a + (b + c) (ii) (a* b) * c = a * (b*c)

Solution: L = (a* b) *c and R a * (b*c)

To prove L = R

i.e., To Prove

a + L = a + R

a + L = a + ((a*b) *c)

= (a + (a * b)) * (a + c)

= a * (a + 1)

= a           [ by Absorption laws]

a + R = a + (a* (b*c))

= (a + a) * (a + (b*c))

= a * (a + (b*c))

= a

Thus a + L = a + R

Next we show that a' + L = a' + R

a' + L = a' + ((a*b) *c)

= (a' + (a * b)) * (a ' + c)

= ((a' + a) * (a' + b)) * (a'+ c)

= (1 * (a' + b)) * (a' + c)

(a' + b) * (a' + c)

= a' + (b*c) …..(1)

Also  a' +R = a' + (a * (b*c))

= (a' + a) * (a' + (b*c))

= 1 * (a' + (b*c))

= a' + (b*c) ….(2)

Thus from (1) and (2) we get

a' + L = a' + R

L = 0 + L = (a* a') + L

= (a + L) * (a' + L)

= (a + R) * (a' + R)

= (a* a') + R

= 0 + R

= R

Hence the proof.

Example 13. Consider the Boolean algebra D₂₁₀

(a) List its elements and draw its diagram.

(b) Find the set A of atoms.

(c) Find two subalgebras with eight elements.

(d) Is X = {1, 2, 6, 210} a sublattice of D₂₁₀? A subalgebra?

(e) Is Y = {1, 2, 3, 6} a sublattice of D₂₁₀ ? A subalgebra ?

Solution :

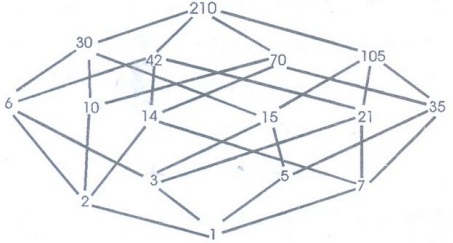
(a) The divisors of 210 are 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105 and 210. The diagram of D₂₁₀ appears in Fig.

(b) A = {2, 3, 5, 7} the set of prime divisors of 210

(c) B = {1, 2, 3, 35, 6, 70, 105, 210} and C = {1, 5, 6, 7, 30, 35, 42, 210} are subalgebras of D₂₁₀

(d) X is a sublattice since it is linearly ordered. However, X is not a subalgebra since 35 is the complement of 2 in D₂₁₀ but 35 does not belong to X.

(e) y is a sublattice of D₂₁₀ since it is closed under + and *. However, Y is not a subalgebra of D₂₁₀ since it is not closed under complements in D210. e.g., 35 = 2' does not belong to Y. (We note that Y itself is a Boolean algebra; in fact, Y = D₆).

Example 14. Find the number of subalgebras of D₂₁₀- A subalgebra of D₂₁₀ must contain two, four, eight or sixteen elements.

(i) There can be only one two-element subalgebra which consists of the upper bound 210 and lower bound 1. i.e., {1, 210}

(ii) Since D210 contains sixteen elements, the only sixteen-element subalgebra is D210 itself.

(iii) Any four-element subalgebra is of the form {1, x, x', 210}, ie., consists of the upper and lower bounds and a nonbound element and its complement. There are fourteen nonbound elements in D210 and so there are 1½ = 7 pairs {x, x'}. Thus D₂₁₀ has seven four-element subalgebras.

Example 18. Show that Every distributive lattice is modular. Whether the converse is true? Justify your claim. [A.U. N/D. 2004] [A.U. M/J. 2006] [A.U N/D 2019, R-17]

Solution :

Proof :

Let (L, ≤) be a distributive lattice

For all a, b, c Є L, we have

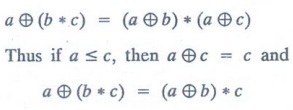
So if a ≤c, the modular equation is satisfied and L is modular.

However, the converse is not true,

Example of lattice which is modular but not a distributive.

M₅ → diamond lattice

In M₅, a v (b^c) = av0 = a while (a v b) ^ (a v c) = |^| = 1

So M₅ is not distributive.

As N₅ is not a sublattice of M₅, M₅ is modular.

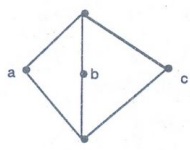
Example 19. In any Boolean algebra, show that

(a + b') (b + c') (c + a') = (a' + b) (b' + c) (c' + a)

LHS = (a + b'+0) (b + c ' + 0) (c + a' + 0).

= (a + b' + c.c'). (b + c' + aa'). (c + a' + bb')

= (a + b' + c). (a + b' + c'). (b + c' + a). (b + c' + a') . (c + a' + b). (c + a' + b')

= {(a' + b + c) (a' + b + c')}. {(b' + c + a) (b' + c + a')} {(c' + a + b) (c' + a + b')}

= (a' + b + cc'). (b' + c + aa'). (c' + a + bb')

= (a' + b + 0). (b' + c + 0). (c' + a + 0)

= (a' + b). (b' + c). (cc' + a)

= RHS.

Example 20. In any Boolean algebra show that   a = 0 ↔ a b' + a' b = b

Solution: If a = 0, clearly ab' + a' b = 0 + 1b = 0 + b = b

Suppose b = a b' + a' b

0 = lb' =b' (ab' + a'b) = ab' + 0 = ab'.

Using De Morgan's, from (1) we obtain

b' = (a' + b) (a + b') …. (1)

0 = ab' = a (a' + b) (a + b') = (aa' + ab) (a + b')

= (0 + ab) (a + b')

= ab (a + b') = aba + abb'

= ab + 0 = ab

0 = ab = ab'

0 = ab + ab' = a (b + b') = al = a

Hence a = 0

Example 21. Prove that D110, the set of all positive divisors of a positive integer 110, is a Boolean algebra and find all its sub algebras. [A.U A/M 2011 R-08]

Solution : Let S = D₁₁₀ = {1, 2, 5, 10, 11, 22, 55, 110}

Then <S, D> is a poset.

a ˄ b = gcd (a, b), a v b = 1cm (a, b)

Thus <S, V, ˄> ↔ is a lattice.

From the Hasse diagram, it is distributive and complemented.

it is a Boolean algebra

with 0 ≡ 1 and 1 ≡ 110

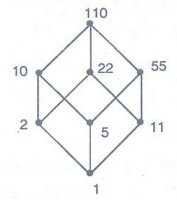
Sub Boolean algebras are {0, 1} ≡ {1, 110}

{1, 2, 5, 10, 11, 22, 55, 110}

{a, a¹, 1, 110} for all a Є S

{1, 110}, {1, 2, 55, 110}

{1, 5, 22, 110} and

{1, 10, 11, 110}; 15 sublattices of 4 elements.

Example 23. In any Boolean algebra, prove that the following statements are equivalent :

(1) a + b = b

(2) a . b = a

(3), a' + b = 1 and

(4) a . b' = 0

Solution: To prove: (1), (2), (3) & (4) are equivalent.

i.e., To prove : (1) ↔ (2), (1) ↔ (3) and (3) ↔ (4)

I. To prove: (1) ↔ (2) i.e., to prove : (1) ⇒ (2), (2) ⇒ (1)

(i) To prove : (1) ⇒ (2)

i.e., Given: a+b = b, to prove a.b=a

Proof: a. b = a. (a + b)

= a.a + a.b     [distributive law]

= a + a.b       [ a.a = a idempotent law]

= a     by Absorption law.

i.e., a .b = a

(ii) To prove : (2) ⇒ (1)

i.e., Given: a.b = a, to prove a + b = b

Proof: a+b = a.b + b

= (a + 1). b [distributive law]

= 1.b   [ a + 1 = 1 boundedness law]

= b    identity law.

From (i) & (ii) we get (1) ↔ (2)

II. To prove: (1) ↔ (3) i.e., to prove (1) ⇒ (3), (3) => (1)

(i) To prove: (1) → (3)

i.e., Given: a+b = b, to prove a' + b = 1

Proof: a' + b = a' + (a + b)

= (a' + a) + b

= 1+b   [Complement law]

= 1    [Boundedness law]

(ii) To prove : (3) => (1)

i.e., Given: a' + b = 1, to prove a + b = b

Proof: a + b = (a + b). 1      identity law

= (a + b). (a' + b)

= a . a' + a . b + b . a' + b . b

= 0 + a . b + b . a' + b [. a.a' = 0, b.b = b]

= b . a + b . a' + b  [a.b = b.a]

= b. [a + a'] + b   ['. a + a' = 1]

= b.1 + b

= b+b

= b   [idempotent law]

From (i) & (ii) we get (1) ↔ (3)

III. To prove (3) ↔ (4) i.e., to prove (3) ⇒ (4), (4) ⇒ (3)

(i) To prove: (3) ⇒ (4)

i.e., Given: a' + b = 1, To prove : a.b' = 0

Proof: a' + b = 1

⇒ (a' + b)' = 1'

(a')'.b' = 0      by Demorgan's law.

a.b' = 0

(ii) To prove: (4) => (3)

i.e., Given: a.b' = 0, to prove: a '+ b = 1

Proof : (a.b')' = 0'

(a')' + (b')' = 1

a' + b = 1      by Demorgans.

From (i) and (ii) we get

(3) ↔ (4)

Hence the proof.

Example 24. In a Boolean algebra, prove that a. (a + b) = a, for all a, b Є B. [A.U N/D 2012 R-08]  

Solution: a . (a + b)

= (a + 0) . (a + b)        by identity law.

= a + 0.b      by distributive law.

= a + b.0     by commutative law.

= a + 0   by dominance law.

= a       by identity law.

Example 25. Simplify the Boolean expression a'.b'.c + a.b'.c + a'.b'.c' using Boolean algebra identities.     [A.U N/D 2012 R-08]

Solution: Given: a'.b'.c + a.b'.c + a.b'.c'

= a'b'.c + a.b'. (c + c')

= a'.b'.c + a.b'.1

= b'. (a + a'.c)

= b'. (a + a'). (a + c)

= b'.1. (a + c)

= a.b' + b'.c

Example 26. Is a Boolean algebra contains six elements? Justify your answer.  [A.U N/D 2015 R-13]

Solution: No, 6 (elements) ≠ 2n (n is +ve integer)

We know that "Every finite Boolean algebra has 2ⁿ elements for some positive integer n.

Example 27. Show that the absorption laws are valid in a Boolean algebra.  [A.U. M/J 2016 R-13]

Solution :

a + ab = a (1 + b)

= a (1)

= a

Example 28. Consider the Lattice D105 with the partial ordered relation divides, then

(1) Draw the Hasse diagram of D₁₀₅

(2) Find the complement of each elements of D₁₀₅

(3) Find the set of atoms of D₁₀₅

(4) Find the number of subalgebras of D₁₀₅         [A.U N/D 2016 R-13]

Solution :

We have 105 = 3x5×7

105 is the product of distinct prime numbers

D₁₀₅ is a Boolean algebra.

D₁₀₅ = {1, 3, 5, 7, 15, 21, 35, 105}

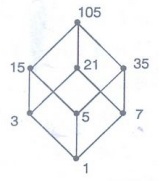
We have 1' = 105, 3' = 35, 5' = 21, 7' = 15, 15' = 7, 35' = 3, 105' = 1

The immediate successors of the lower bound '1' are 3, 5, 7

The atoms of D₁₀₅ are 3, 5, 7

O (D₁₀₅) = 2³ = 8

A subalgebra of D₁₀₅ can have 2 or 4 or 8 elements

{1, 105} and D105 are subalgebras of order 2 and 8 respectively.

Let {1, x, x', 105} be a sub algebra of B₁₀₅ of order 4.

x can be either 3 or 5 or 7.

Example 29. Determine whether D₈ is a Boolean algebra. [A.U. N/D 2018 R-17]

Solution :

D₈ = {1, 2, 4, 8}

D₈ is not a Boolean algebra.

Since 2 and 4 has no complements.

Example 30. Show that D₃₀ is a Boolean algebra. Draw Hasse diagram of D₃₀. Find the complements, atoms and subalgebras of D₃₀.

Solution: Here D₃₀ = {1, 2, 3, 5, 6, 10, 15, 30}

Now, 30 2 ˟ 3 ˟ 5

D₃₀ is the product of distinct prime numbers

D₃₀ is a Boolean algebra.

The Hasse diagram of D₃₀ is shown in the adjoining figure.

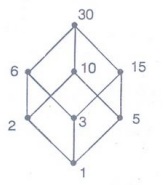
Now, 1' = 30, 2' = 15, 3' = 10, 5' = 6, 6' = 5, 10' = 3, 15' = 2 and 30' = 1

The immediate successors of the lower bound 1 and 2, 3 and 5.

The atoms of D₃₀ are 2, 3 and 5.

Number of elements in D₃₀ = 2³ = 8.

A subalgebra of D₃₀ can have 2 or 4 or 8 elements.

Also, {1, 30} and D₃₀ are subalgebras of order 2 and 8 respectively.

Let {1, x, x', 30} be a subalgebra of D₃₀ of order 4.

x can take either 2 or 3 or 5.

The subalgebras of D₃₀ of order 4 are

{1, 2, 15, 30}, {1, 3, 10, 30} and {1, 5, 6, 30}.

The subalgebras of D₃₀ are {1, 30}, {1, 2, 15, 30}, {1, 3, 10, 30}, {1, 5, 6, 30} and D₃₀.

Example 31. Show that a lattice homomorphism on a Boolean algebra which preserves 0 and 1 is a Boolean homomorphism.      [A.U N/D 2013 R8/R10]

Solution: Let f be a lattice homomorphism from (A, ˄, V, ', 0, 1) to (B, +,., -, α, ẞ).

As f preserves 0 and 1.

f (0) = α and ƒ (1) = β

α = ƒ (0) = f (a ˄ a') = f (a) . f (a')

ẞ = f(1) = f (a v a') = f (a) + f (a')

So, f(a') = f (ā),

→ f preserves complementation.

As a lattice homomorphism, f preserves the join operation.

Hence, ƒ is a Boolean algebra homomorphism.

EXERCISE 5.3