Binary Adder Subtractor

Binary Adder Subtractor

AU: Dec.-07.08,09,10,11,12,15,16,19, May-03,06,09,10,11,12,13,15, 16,19

Adders

• The most basic operation, is the addition of two binary digits.

• The simple addition consists of four possible elementary operations, namely,

0+0=0

0+1 = 1

1 +0 = 1

1+ 1 = 10₂

• The first three operations produce a sum whose length is one digit, but when the last operation is performed sum is two digits. The higher significant bit of this result is called a carry, and lower significant bit is called sum.

• The logic circuit which performs this operation is called a half-adder.

• The circuit which performs addition of three bits (two significant bits and a previous carry) is a full-adder.

Half Adder

• The half-adder operation needs two binary inputs: augend and addend bits; and two binary outputs: sum and carry.

• The truth table shown in Table 1.12.1 gives the relation between input and output variables for half-adder operation.

Limitations of Half-Adder :

In multidigit addition we have to add two bits along with the carry of previous digit addition. Effectively such addition requires addition of three bits. This is not possible with half-adder. Hence half-adders are not used in practice.

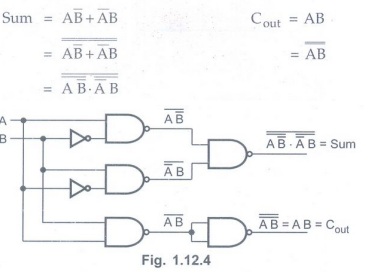
Example 1.12.1 Draw half adder using NAND gates.

Solution: For half adder:

Full Adder

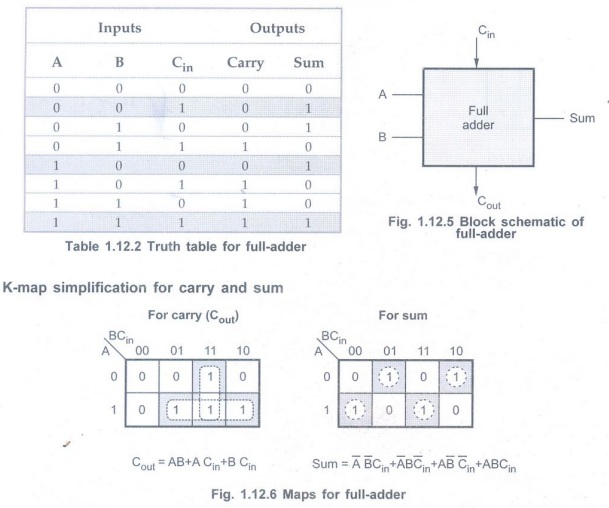
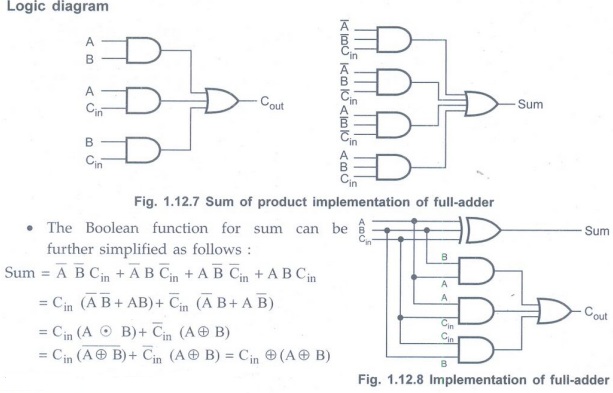
• A full-adder is a combinational circuit that forms the arithmetic sum of three input bits.

• It consists of three inputs and two outputs.

• Two of the input variables, denoted by A and B, represent the two significant bits to be added. The third input C_in, represents the carry from the previous lower significant position.

• The truth table for full-adder is shown in Table 1.12.2.

Review Questions

1. Design half-adder using only NAND gates.

2. Draw the truth table of half adder.  AU Dec.-15. Marks 2

3. Design full-adder using only NOR gates.

4. Design full adder using two half adders and OR gate.  AU May-19, Marks 2

5. Design a full adder with inputs x, y, z and two outputs S and C. The circuits performs x + y + z, z is the input carry, C is the output carry and S is the sum.   AU May-16, Marks 16

Subtractors

• The subtraction consists of four possible elementary operations, namely,

0 0 = 0

0-1 = 1 with 1 borrow

1-0= 1

1-1 = 0

• In all operations, each subtrahend bit is subtracted from the minuend bit.

• In case of second operation the minuend bit is smaller than the subtrahend bit, hence 1 is borrowed.

Half Subtractor

• A half-subtractor is a combinational circuit that subtracts two-bits and produces their difference.

• It also has an output to specify if a 1 has been borrowed.

• Let us designate minuend bit as A and the subtrahend bit as B. The result of operation A – B for all possible values of A and B is tabulated in Table 1.12.3.

• The Boolean expression for the outputs of half-subtractor can be determined as follows.

Limitations of half-subtractor :

In multidigit subtraction, we have to subtract two bits along with the borrow of the previous digit subtraction. Effectively such subtraction requires subtraction of three bits. This is not possible with half-subtractor.

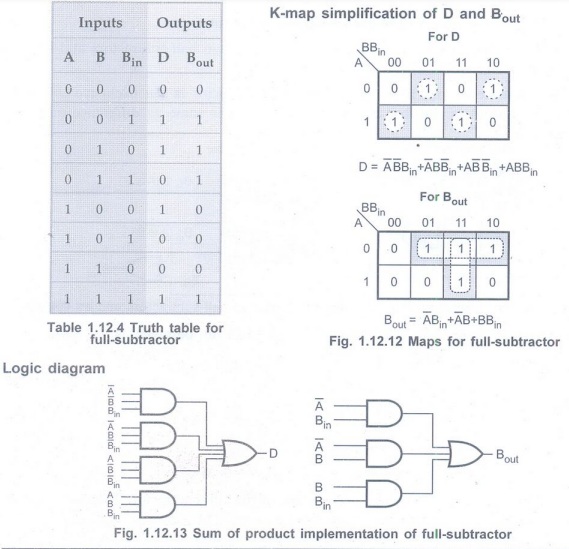
Full Subtractor

• A full-subtractor is a combinational circuit that performs a subtraction between two bits, taking into account borrow of the lower significant stage.

• This circuit has three inputs and two outputs.

• The three inputs are A, B and, B_in denote the minuend, subtrahend, and previous borrow, respectively.

• The two outputs, D and Bout represent the difference and output borrow, respectively.

• The Table 1.12.4 shows the truth table for full-subtractor.

• The Boolean function for D (difference) can be further simplified as follows:

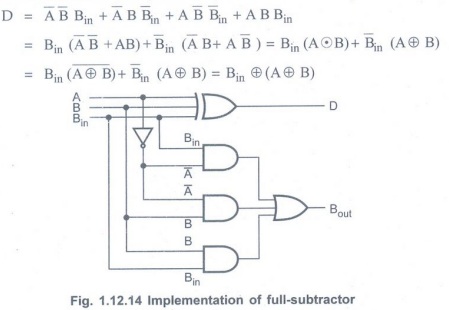
• full subtractor can also be implemented with two half-subtractors and one OR gate, as shown in the Fig. 1.12.15.

• The difference output from the second half-subtractor is the exclusive-OR of and the output of the first half-subtractor, which is same as difference output of full-subtractor.

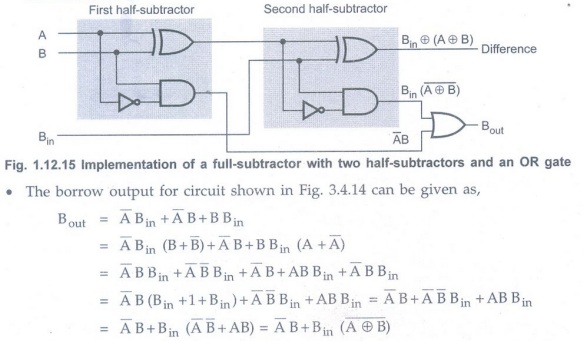
This Boolean function is same as borrow out of the full-subtractor. Therefore, we can implement full-subtractor using two half-subtractors and OR gate.

Review Questions

1. Explain the circuit diagram of full-subtractor.

2. Design half subtractor and full subtractor circuit and implement using NAND gate.

3. Design a full subtractor and derive expression for difference and borrow. Realize using gates.  AU: Dec.-15, Marks 16

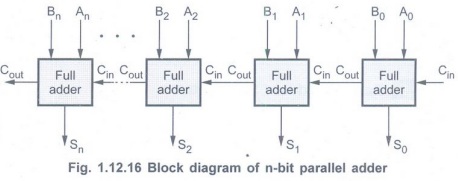
Parallel Adder

• In order to add binary numbers with more than one bit, additional full-adders must be employed.

• A n-bit, parallel adder can be constructed using number of full adder circuits connected in parallel.

• Fig. 1.12.16 shows the block diagram of n-bit parallel adder using number of full-adder circuits connected in cascade, i.e. the carry output of each adder is connected to the carry input of the next higher-order adder.

• It should be noted that either a half-adder can be used for the least significant position or the carry input of a full-adder is made 0 because there is no carry into the least significant bit position.

Example 1.12.2 Design a 4-bit parallel adder using full-adders.

Solution: Fig.1.12.17 shows the block diagram for 4-bit adder. Here, for least significant position, carry input of full-adder is made 0.

Review Question

1. Draw and explain the block diagram of 4-bit parallel adder.

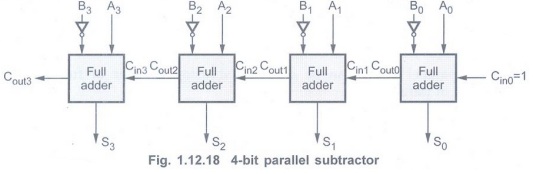
Parallel Subtractor

• The subtraction of binary numbers can be done most conveniently by means of complements.

• The subtraction A-B can be done by taking the 2's complement of B and adding it to A.

• The 2's complement can be obtained by taking the 1's complement and adding one to the least significant pair of bits.

• The 1's complement can be implemented with inverters and a one can be added to the sum through the input carry, as shown in the Fig. 1.12.18.

Review Question

1. Draw and explain the block diagram of 4-bit parallel subtractor.

Parallel Adder / Subtractor

• The addition and subtraction operations can be combined into one circuit with one common binary adder. This is done by including an exclusive-OR gate with each full adder, as shown in Fig. 1.12.19.

• The mode input M controls the operation of the circuit. When M = 0, the circuit is an adder, and when M = 1, the circuit becomes a subtractor.

• Each exclusive - OR gate receives input M and one of the inputs of B.

• The B inputs are all complemented and a 1 is added through the input carry.

• The circuit performs the operation A plus the 2's complement of B, i.e. A - B.

• The parallel adder is ripple carry adder in which the carry output of each full-adder stage is connected to the carry input of the next higher-order stage. Therefore, the sum and carry outputs of any stage cannot be produced until the input carry occurs; this leads to a time delay in the addition process. This delay is known as carry propagation delay.

• One method of speeding up this process by eliminating inter stage carry delay is called look ahead-carry addition. This method utilizes logic gates to look at the lower-order bits of the augend and addend to see if a higher-order carry is to be generated.

Review Question

1. Design of 4 bit binary adder-subtractor circuit.  AU May-19, Dec.-19, Marks 8

Look-Ahead Carry Adder

The parallel adder discussed in the last paragraph is ripple carry type in which the carry output of each full-adder stage is connected to the carry input of the next higher-order stage. Therefore, the sum and carry outputs of any stage cannot be produced until the input carry occurs; this leads to a time delay in the addition process. This delay is known as carry propagation delay, which can be best explained by considering the following addition.

0101

0011 +

1000

Addition of the LSB position produces a carry into the second position. This carry, when added to the bits of the second position (stage), produces a carry into the third position. The latter carry, when added to the bits of the third position, produces a carry into the last position. The key thing to notice in this example is that the sum bit generated in the last position (MSB) depends on the carry that was generated by the addition in the previous positions. This means that, adder will not produce correct result until LSB carry has propagated through the intermediate full-adders. This represents a time delay that depends on the propagation delay produced in an each full-adder. For example, if each full-adder is considered to have a propagation delay of 30 ns, then S₃ will not reach its correct value until 90 ns after LSB carry is generated. Therefore, total time required to perform addition is 90+30 = 120 ns.

Obviously, this situation becomes much worse if we extend the adder circuit to add a greater number of bits. If the adder were handling 16-bit numbers, the carry propagation delay could be 480 ns.

One method of speeding up this process by eliminating inter stage carry delay is called look ahead-carry addition. This method utilizes logic gates to look at the lower-order bits of the augend and addend to see if a higher-order carry is to be generated. It uses two functions: carry A- generate and carry propagate.

Consider the circuit of the full-adders shown in Fig. 1.12.20. Here, we define two functions:carry generate and carry propagate.

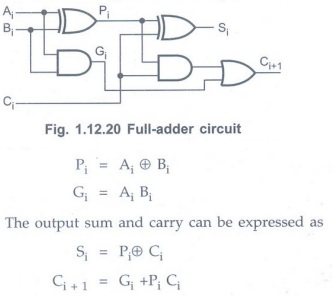
G_i is called a carry generate and it produces on carry when both A_i and B_i are one, regardless of the input carry. P_i is called a carry propagate because it is term associated with the propagation of the carry from C_i to C_i+1

Now the Boolean function for the carry output of each stage can be written as follows.

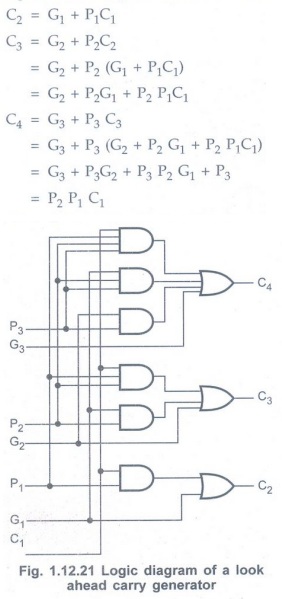
From the above Boolean function it can beseen that C₄ does not have to wait for C₃ and C₂ to propagate; in fact C₄ is propagated at the same time as C₂ and C₃.

The Boolean functions for each output carry are expressed in sum-of product form, thus they can be implemented using AND-OR logic or NAND-NAND logic. Fig 1.12.21 shows implementation of Boolean functions for C₂, C₃ and C₄ using AND-OR logic.

Using a look ahead carry generator we can easily construct a 4-bit parallel adder with a look ahead carry scheme. Fig. 1.12.22 shows a 4-bit parallel adder with a look ahead carry scheme. As shown in the Fig. 1.12.22, each sum output requires two exclusive-OR gates. The output of first exclusive-OR gate generates P_i, and the AND gate generates G_i.The carries are generated using look ahead carry generator and applied as inputs to the second exclusive-OR gate. Other inputs to exclusive-OR gate is p_i. Thus second exclusive-OR gate generates sum outputs. Each output each generated after a delay of two levels of gate. Thus outputs S₂ through S₄ have equal propagation delay times.

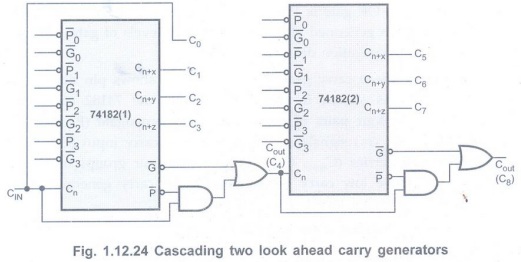
Example 1.12.3 Construct the look ahead carry generator to accommodate higher word size. AU: Dec.-11, Marks 8

Solution: Look ahead carry generators can be cascaded to increase the word size in multiples of 4-bits. Fig. 1.12.24 shows the cascading two look ahead carry generators (IC 74182s) to get word size of 8-bits.

Review Question

1. With neat diagram explain the 4-bit adder with carry lookahead.  AU May-15, Dec.-16, Marks 8

Serial Adder

The Fig. 1.12.25 shows the logic diagram of serial adder. Using the logic diagram shown in Fig. 1.12.25 we can add numbers stored in the right shift registers A and B, serially. (Readers are suggested to read details of shift register and D-flip-flop from chapters 4 and 6, respectively). The full-adder is used to perform bit by bit addition and D-flip-flop is used to store the carry output generated after addition. This carry is used as carry input for the next addition. Initially,D-flip-flop is cleared and addition starts with the least significant bits of both register.After each clock pulse data within the right shift registers are shifted right 1-bit and we get bits from next digit and carry of previous addition as new inputs for the full-adder.The result SUM is stored bit by bit in the register A.

 

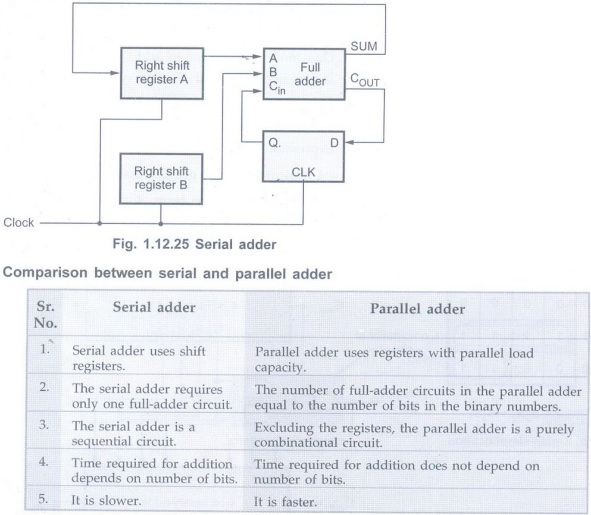
We can implement serial subtractor by replacing full-subtractor instead of full-adder in the Fig. 1.12.25. Here, we will get difference and borrow instead of sum and carry.

Review Questions

1. Design a serial adder using a full adder and a flip flop.   AU Dec.-15, Marks 16

2. With diagram explain how two binary numbers are added serially using shift registers.  AU: Dec.-19, Marks 6

Decimal / BCD Adder

• A BCD adder is a circuit that adds two BCD digits and produces a sum digit also in BCD.

• To implement BCD adder we require :

• 4-bit binary adder for initial addition

• Logic circuit to detect sum greater than 9 and

• One more 4-bit adder to add  in the sum if sum is greater than 9 or carry is 1.

• The logic circuit to detect sum greater than 9 can be determined by simplifying the boolean expression of given truth table.

• Y = 1 indicates sum is greater than 9.

• We can put one more term,  in the above expression to check whether carry is one.

• If any one condition is satisfied we add 6(0110)in the sum.

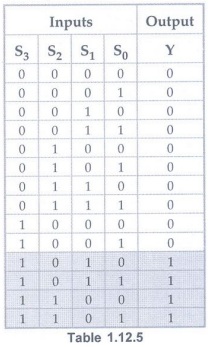
• As shown in the Fig. 1.12.26 (b), the two BCD numbers, together with input carry, are first added in the top 4-bit binary adder to produce a binary sum.

• When the output carry is equal to zero (i.e. when sum ≤ 9 and  = 0) nothing (zero) is added to the binary sum.

• When the output carry is equal to one (i.e. when sum > 9 or  = 1), binary 0110 is added to the binary sum through the bottom 4-bit binary adder.

• The output carry generated from the bottom binary adder can be ignored, since it supplies information already available at the output-carry terminal.

Example 1.12.4 Design an 8-bit BCD adder using 4-bit binary adder.

Solution: To implement 8-bit BCD adder we have to cascade two 4-bit BCD adders. In cascade connection carry output of the lower position (digit) is connected as a carry input of the higher position (digit). Fig. 1.12.27 shows the block diagram of 8-bit BCD adder.

Example 1.12.5 Design a BCD to Ex-3 code converter using binary parallel adder.

Solution :

Review Questions

1. Explain with suitable example rules for BCD addition and design 1-digit BCD adder using IC 74LS83.

2. Draw and explain the basic circuit of single digit BCD adder using IC 7483. How will you make two digit BCD adder? Explain the logic of the circuit.

3. What is BCD adder? Design an adder to perform arithmetic addition of two decimal digits in BCD.  AU Dec.-19, Marks 13

4. How will make 3-digit BCD adder using 4-bit binary adder as a basic building block? Explain with the help of suitable diagram.

5. Draw and explain 4-bit BCD adder using IC 7483. Also explain with reference to your design addition of  and .

6. Draw and explain 4-bit BCD adder using IC 7483. Also explain with example addition of numbers with carry.

BCD Subtractor

Addition of signed BCD numbers can be performed by using 9's or 10's complement methods. A negative BCD number can be expressed by taking the 9's or 10's complement. Let us see the implementation of subtraction process using 9's and 10's complement methods.

Subtractor using 9's Complement Method

The steps for 9's complement BCD subtraction as follows:

•Find the 9's complement of a negative number

•Add two numbers using BCD addition

• If carry is generated add carry to the result otherwise find the 9's complement of the result.

Fig. 1.12.29 shows the logic diagram of the circuit to implement above mentioned steps to perform BCD subtraction using 9's complement method. As shown in the

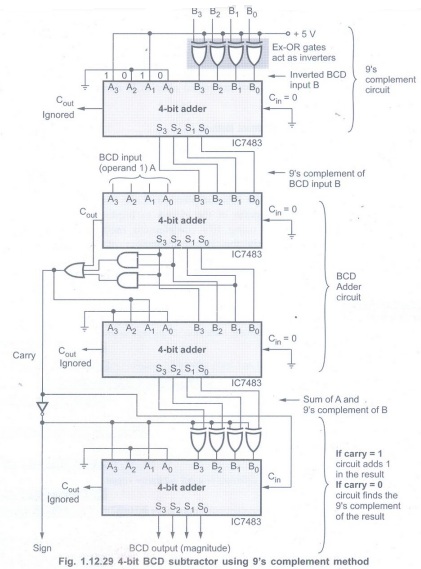
Fig. 1.12.29, first binary adder finds the 9's complement of the negative number. It does this by inverting each bit of BCD number and adding 10 (1 0 1 02) to it. Let us find the 9's complement of 2

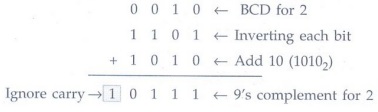
Next two 4-bit binary adders perform the BCD addition. The last adder finds the 9's complement of the result if carry is not generated after BCD addition otherwise it adds carry in the result.

Subtractor using 10's Complement Method

The steps for 10's complement BCD subtraction as follows.

• Find the 10's complement of a negative number

• Add two numbers using BCD addition

• If carry is not generated find the 10's complement of the result.

Fig. 1.12.30 shows the logic diagram of the circuit to implement above mentioned steps to perform BCD subtraction using 10's complement method. As shown in the Fig. 1.12.30, first binary adder finds the 10's complement of the negative number (9's complement + 1). Next two 4-bit binary adders perform the BCD addition. Finally, last 4-bit binary adder finds the 10's complement of the number if carry is not generated after BCD addition. (See Fig. 1.12.30 on next page)

Review Questions

1. Draw a block diagram of half adder. Write truth table. Draw logic diagram. AU May-06, Marks 2

2. Define full adder. Draw logic circuit and truth table of full adder. AU Dec.-10, Marks 6

3. Implement full adder using two half adders. AU: Dec.-07, May-11, 13, Dec.-12, Marks 8.

4. Draw the schematic of a full adder circuit and give its truth table. AU May-11, Marks 6

5. Design a half-subtractor combinational circuit to produce the outputs. Difference and borrow. AU: Dec.-10, May-12, Marks 2

6. Write the logic expressions for the difference and borrow of a half subtractor.  AU May-11, Marks 2

7. Write an expression for borrow and difference in a full subtractor circuit. AUMay-10, Marks 2

8. Design full-subtractor circuit and draw necessary truth tables. AU: May-03, May-12, Marks 7

9. What is the drawback in binary parallel adder? How can it be rectified? AU Dec.-07, Marks 3

10. Draw the block diagram of a 2's complement adder/subtractor. AU: May-03, Marks 2

11. Draw the diagram of a 4-bit adder subtractor using full adders. AU: Dec.-12, Marks 4

12. Relate carry generate, carry propagate, sum and carry-out of a carry look ahead adder. AU: Dec.-10, Marks 2

13. Compare the performance of binary serial adder and parallel adders.  AU: Dec.-11, Marks 2

14. With a suitable block diagram explain the operation of BCD adder. AU May-09, Dec.-12, Marks 16

15. With neat diagram explain BCD subtractor using 9's and 10's complement method. AU: Dec.-09, Marks 16

16. Design a combinational circuit that generates the 9's complement of a BCD digit. AU: Dec.-08, Marks 8