Basic Statistical Descriptions of Data

Basic Statistical Descriptions of Data

• For data preprocessing to be successful, it is essential to have an overall picture of our data. Basic statistical descriptions can be used to identify properties of the data and highlight which data values should be treated as noise or outliers.

• Basic statistical descriptions can be used to identify properties of the data and highlight which data values should be treated as noise or outliers.

• For data preprocessing tasks, we want to learn about data characteristics regarding both central tendency and dispersion of the data.

• Measures of central tendency include mean, median, mode and midrange.

• Measures of data dispersion include quartiles, interquartile range (IQR) and variance.

• These descriptive statistics are of great help in understanding the distribution of the data.

Measuring the Central Tendency

• We look at various ways to measure the central tendency of data, include: Mean, Weighted mean, Trimmed mean, Median, Mode and Midrange.

1. Mean :

• The mean of a data set is the average of all the data values. The sample mean x is the point estimator of the population mean μ.

2. Median :

Sum of the values of then observations Number of observations in the sample

Sum of the values of the N observations Number of observations in the population

• The median of a data set is the value in the middle when the data items are arranged in ascending order. Whenever a data set has extreme values, the median is the preferred measure of central location.

• The median is the measure of location most often reported for annual income and property value data. A few extremely large incomes of property values can inflate the mean.

• For an off number of observations:

7 observations= 26, 18, 27, 12, 14, 29, 19.

Numbers in ascending order = 12, 14, 18, 19, 26, 27, 29

• The median is the middle value.

    Median=19

• For an even number of observations :

  8 observations = 26 18 29 12 14 27 30 19

Numbers in ascending order =12, 14, 18, 19, 26, 27, 29, 30

The median is the average of the middle two values.

3. Mode:

• The mode of a data set is the value that occurs with greatest frequency. The greatest frequency can occur at two or more different values. If the data have exactly two modes, the data have exactly two modes, the data are bimodal. If the data have more than two modes, the data are multimodal.

• Weighted mean: Sometimes, each value in a set may be associated with a weight, the weights reflect the significance, importance or occurrence frequency attached to their respective values.

• Trimmed mean: A major problem with the mean is its sensitivity to extreme (e.g., outlier) values. Even a small number of extreme values can corrupt the mean. The trimmed mean is the mean obtained after cutting off values at the high and low extremes.

• For example, we can sort the values and remove the top and bottom 2 % before computing the mean. We should avoid trimming too large a portion (such as 20 %) at both ends as this can result in the loss of valuable information.

• Holistic measure is a measure that must be computed on the entire data set as a whole. It cannot be computed by partitioning the given data into subsets and merging the values obtained for the measure in each subset.

Measuring the Dispersion of Data

• An outlier is an observation that lies an abnormal distance from other values in a random sample from a population.

• First quartile (Q₁): The first quartile is the value, where 25% of the values are smaller than Q₁ and 75% are larger.

• Third quartile (Q₃): The third quartile is the value, where 75 % of the values are smaller than Q₃ and 25% are larger.

• The box plot is a useful graphical display for describing the behavior of the data in the middle as well as at the ends of the distributions. The box plot uses the median and the lower and upper quartiles. If the lower quartile is Q₁ and the upper quartile is Q₃, then the difference (Q₃ - Q₁) is called the interquartile range or IQ.

• Range: Difference between highest and lowest observed values

Variance :

• The variance is a measure of variability that utilizes all the data. It is based on the difference between the value of each observation (x;) and the mean (x) for a sample, u for a population).

• The variance is the average of the squared between each data value and the mean.

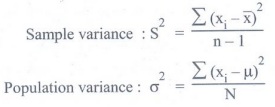
Standard Deviation :

• The standard deviation of a data set is the positive square root of the variance. It is measured in the same in the same units as the data, making it more easily interpreted than the variance.

• The standard deviation is computed as follows:

Difference between Standard Deviation and Variance

Graphic Displays of Basic Statistical Descriptions

• There are many types of graphs for the display of data summaries and distributions, such as Bar charts, Pie charts, Line graphs, Boxplot, Histograms, Quantile plots and Scatter plots.

1. Scatter diagram

• Also called scatter plot, X-Y graph.

• While working with statistical data it is often observed that there are connections between sets of data. For example the mass and height of persons are related, the taller the person the greater his/her mass.

• To find out whether or not two sets of data are connected scatter diagrams can be used. Scatter diagram shows the relationship between children's age and height.

• A scatter diagram is a tool for analyzing relationship between two variables. One variable is plotted on the horizontal axis and the other is plotted on the vertical axis.

• The pattern of their intersecting points can graphically show relationship patterns. Commonly a scatter diagram is used to prove or disprove cause-and-effect relationships.

• While scatter diagram shows relationships, it does not by itself prove that one variable causes other. In addition to showing possible cause and effect relationships, a scatter diagram can show that two variables are from a common cause that is unknown or that one variable can be used as a surrogate for the other.

2. Histogram

• A histogram is used to summarize discrete or continuous data. In a histogram, the data are grouped into ranges (e.g. 10-19, 20-29) and then plotted as connected bars. Each bar represents a range of data.

• To construct a histogram from a continuous variable you first need to split the data into intervals, called bins. Each bin contains the number of occurrences of scores in the data set that are contained within that bin.

• The width of each bar is proportional to the width of each category and the height is proportional to the frequency or percentage of that category.

3. Line graphs

• It is also called stick graphs. It gives relationships between variables.

• Line graphs are usually used to show time series data that is how one or more variables vary over a continuous period of time. They can also be used to compare two different variables over time.

• Typical examples of the types of data that can be presented using line graphs are monthly rainfall and annual unemployment rates.

• Line graphs are particularly useful for identifying patterns and trends in the data such as seasonal effects, large changes and turning points. Fig. 1.12.1 show line graph. (See Fig. 1.12.1 on next page)

• As well as time series data, line graphs can also be appropriate for displaying data that are measured over other continuous variables such as distance.

• For example, a line graph could be used to show how pollution levels vary with increasing distance from a source or how the level of a chemical varies with depth of soil.

• In a line graph the x-axis represents the continuous variable (for example year or distance from the initial measurement) whilst the y-axis has a scale and indicated the measurement.

• Several data series can be plotted on the same line chart and this is particularly useful for analysing and comparing the trends in different datasets.

• Line graph is often used to visualize rate of change of a quantity. It is more useful when the given data has peaks and valleys. Line graphs are very simple to draw and quite convenient to interpret.

4. Pie charts

• A type of graph is which a circle is divided into sectors that each represents a proportion of whole. Each sector shows the relative size of each value.

• A pie chart displays data, information and statistics in an easy to read "pie slice" format with varying slice sizes telling how much of one data element exists.

• Pie chart is also known as circle graph. The bigger the slice, the more of that particular data was gathered. The main use of a pie chart is to show comparisons. Fig. 1.12.2 shows pie chart. (See Fig. 1.12.2 on next page)

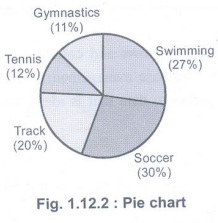
• Various applications of pie charts can be found in business, school and at home. For business pie charts can be used to show the success or failure of certain products or services.

• At school, pie chart applications include showing how much time is allotted to each subject. At home pie charts can be useful to see expenditure of monthly income in different needs.

• Reading of pie chart is as easy figuring out which slice of an actual pie is the biggest.

Limitation of pie chart:

• It is difficult to tell the difference between estimates of similar size.

Error bars or confidence limits cannot be shown on pie graph.

Legends and labels on pie graphs are hard to align and read.

• The human visual system is more efficient at perceiving and discriminating between lines and line lengths rather than two-dimensional areas and angles.

• Pie graphs simply don't work when comparing data.