B+ Tree Index Files

B+ Tree Index Files

AU: May-03,06,16,19, Dec.-17, Marks 16

• The B+ tree is similar to binary search tree. It is a balanced tree in which the internal nodes direct the search.

• The leaf nodes of B+ trees contain the data entries.

Structure of B+ Tree

• The typical node structure of B+ node is as follows –

• It contains up to n – 1 search-key values k₁, k₂, ……, k_n-1 and n pointers

P₁, P₂,..., P_n 

• The search-key values within a node are kept in sorted order; thus, if i < j, then K_i<K_j.

• To retrieve all the leaf pages efficiently we have to link them using page pointers. The sequence of leaf pages is also called as sequence set.

• Following Fig. 4.8.1 represents the example of B+ tree.

• The B+ tree is called dynamic tree because the tree structure can grow on insertion of records and shrink on deletion of records.

Characteristics of B+ Tree

Following are the characteristics of B+ tree.

1) The B+ tree is a balanced tree and the operations insertions and deletion keeps the tree balanced.

2) A minimum occupancy of 50 percent is guaranteed for each node except the root.

3) Searching for a record requires just traversal from the root to appropriate leaf.

Insertion Operation

Algorithm for insertion :

Step 1: Find correct leaf L.

Step 2: Put data entry onto L.

i) If L has enough space, done!

ii) Else, must split L (into L and a new node L2)

• Allocate new node

• Redistribute entries evenly

• Copy up middle key.

• Insert index entry pointing to L2 into parent of L.

Step 3: This can happen recursively

i) To split index node, redistribute entries evenly, but push up middle key. (Contrast with leaf splits.)

Step 4: Splits "grow" tree; root split increases height.

i) Tree growth: gets wider or one level taller at top.

Example 4.8.1 Construct B+ tree for following data. 30,31,23,32,22,28,24,29, where number of pointers that fit in one node are 5.

Solution: In B+ tree each node is allowed to have the number of pointers to be 5. That means at the most 4 key values are allowed in each node.

Step 1: Insert 30,31,23,32. We insert the key values in ascending order.

Step 2: Now if we insert 22, the sequence will be 22, 23, 30, 31, 32. The middle key 30, will go up.

Step 3: Insert 28,24. The insertion is in ascending order.

Step 4: Insert 29. The sequence becomes 22, 23, 24, 28, 29. The middle key 24 will go up. Thus we get the B+ tree.

Example 4.8.2 Construct B+ tree to insert the following (order of the tree is 3) 26,27,28,3,4,7,9,46,48,51,2,6

Solution:

Order means maximum number of children allowed by each node. Hence order 3 means at the most 2 key values are allowed in each node.

Step 1: Insert 26, 27 in ascending order

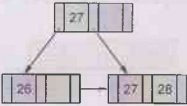
Step 2: Now insert 28. The sequence becomes 26,27,28. As the capacity of the node is full, 27 will go up. The B+ tree will be,

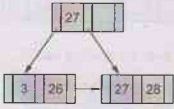
Step 3: Insert 3. The partial B+ Tree will be,

Step 4: Insert 4. The sequence becomes 3,4, 26. The 4 will go up. The partial B+ tree will be –

Step 5: Insert 7. The sequence becomes 4,7,26. The 7 will go up. Again from 4,7,27. the 7 will go up. The partial B+ Tree will be,

Step 6: Insert 9. By inserting 7,9, 26 will be the sequence. The 9 will go up. The partial B+ tree will be,

Step 7: Insert 46. The sequence becomes 27,28,46. The 28 will go up. Now the sequence becomes 9, 27, 28. The 27 will go up and join 7. The B+ Tree will be,

Step 8: Insert 48. The sequence becomes 28,46,48. The 46 will go up. The B+ Tree will become,

Step 9: Insert 51. The sequence becomes 46,48,51. The 48 will go up. Then the sequence becomes 28, 46, 48. Again the 46 will go up. Now the sequence becomes 7,27, 46. Now the 27 will go up. Thus the B+ tree will be

Step 10: Insert 2. The insertion is simple. The B+ tree will be,

Step 11: Insert 6. The insertion can be made in a vacant node of 7(the leaf node). The final B+ tree will be,

Deletion Operation

Algorithm for deletion:

Step 1: Start at root, find leaf L with entry, if it exists.

Step 2: Remove the entry.

i) If L is at least half-full, done!

ii) If L has only d-1 entries,

• Try to re-distribute, borrowing keys from sibling.

(adjacent node with same parent as L).

• If redistribution fails, merge L and sibling.

Step 3: If merge occurred, must delete entry (pointing to L or sibling) from parent of L.

Step 4: Merge could propagate to root, decreasing height.

Example 4.8.3 Construct B+ Tree for the following set of key values

(2,3,5,7,11,17,19,23,29,31) Assume that the tree is initially empty and values are added in ascending order. Construct B+ tree for the cases where the number of pointers that fit one node is four. After creation of B+ tree perform following series of operations:

(a) Insert 9. (b) Insert 10. (c) Insert 8. (d) Delete 23. (e) Delete 19.

Solution: The number of pointers fitting in one node is four. That means each node contains at the most three key values.

Step 1: Insert 2, 3, 5.

Step 2: If we insert 7, the sequence becomes 2, 3, 5, 7. Since each node can accommodate at the most three key, the 5 will go up, from the sequence 2, 3, 5, 7.

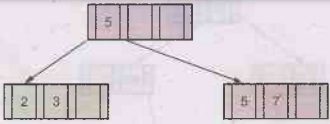
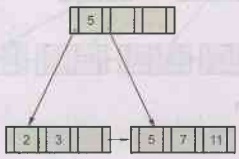
Step 3: Insert 11. The partial B+ tree will be,

Step 4: Insert 17. The sequence becomes 5,7, 11,17. The element 11 will go up. Then the partial B+ tree becomes,

Step 5: Insert 19.

Step 6: Insert 23. The sequence becomes 11,17,19,23. The 19 will go up.

Step 7: Insert 29. The partial B+ tree will be,

Step 8: Insert 31. The sequence becomes 19,23,29, 31. The 29 will go up. Then at the upper level the sequence becomes 5,11,19,29. Hence again 19 will go up to maintain the capacity of node (it is four pointers three key values at the most). Hence the complete B+ tree will be,

(a) Insertion of 9: It is very simple operation as the node containing 5,7 has one space vacant to accommodate. The B+ tree will be,

(b) Insert 10: If we try to insert 10 then the sequence becomes 5,7,9,10. The 9 will go up. The B+ tree will then become –

(c) Insert 8: Again insertion of 8 is simple. We have a vacant space at node 5,7. So we just insert the value over there. The B+ tree will be-

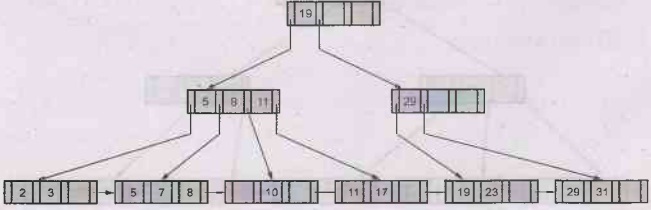
(d) Delete 23: Just remove the key entry of 23 from the node 19,23. Then merge the sibling node to form a node 19,29,31. Get down the entry of 11 to the leaf node. Attach the node of 11,17 as a left child of 19.

(e) Delete 19: Just delete the entry of 19 from the node 19,29,31. Delete the internal node key 19. Copy the 29 up as an internal node as it is an inorder successor node.

Search Operation

1. Perform a binary search on the records in the current node.

2. If a record with the search key is found, then return that record.

3. If the current node is a leaf node and the key is not found, then report an unsuccessful search.

4. Otherwise, follow the proper branch and repeat the process.

For example-

Consider the B+ tree as shown in above Fig. 4.8.2.

For searching a node 25, we start from the root node -

(1) Compare 20 with key value 25. As 25>20, move on to right branch.

(2) Compare 25 with key value 25. As the match is found we declare, that the given node is present in the B+ tree.

For searching a node 10, we start form the root node -

(1) Compare 20 with key value 10, as 10<20, we follow left branch

(2) Compare 8 with 10, 10>8, then we compare 10 with the next adjacent value of the same node. It is 11, as 10<11, we follow left branch of 11.

(3) We compare 10, with all the values in that node, as match is not found we report unsuccessful search or node is not present in given B+ tree.

Merits of B+ Index Tree Structure

1. In B+ tree the data is stored in leaf node so searching of any data requires scanning only of leaf node alone.

2. Data is ordered in linked list.

3. Any record can be fetched in equal number of disk accesses.

4. Range queries can be performed easily as leaves are linked up.

5. Height of the tree is less as only keys are used for indexing.

6. Supports both random and sequential access.

Demerits of B+ Index Tree Structure

1. Extra insertion of non leaf nodes.

2. There is space overhead.

Review Questions

1. Explain the B+ tree indexes on multiple keys with suitable example. AU: Dec.- 17, Marks 7

2. Briefly explain about B+ index file with example. AU: May-16, Marks 16

3. What are the merits and demerits of B+ tree index structures. AU: May-03, Marks 4

4. Describe structure of B+ tree and list the characteristics of B+ tree.

Implementation Techniques  AU: May-03, Marks 6. May-06, Marks 8

5. Describe the structure of B+ tree and give the algorithm for search in the B+ tree with example.   AU: May-19, Marks 13