AVL Trees

 AVL Trees

Adelsion Velski and Lendis in 1962 introduced binary tree structure that is balanced with respect to height of subtrees. The tree can be made balanced and because of this retrieval of any node can be done in O(logn) times, where n is total number of nodes. From the name of these scientists the tree is called AVL tree.

• Definition

An empty tree is height balanced if T is a non empty binary tree with T_L and T_R as its left and right subtrees. The T is height balanced if and only if,

i) T_L and T_R are height balanced.

ii) H_L - h_R <=1 where h_L - h_R are heights of T_L and T_R

The idea of balancing a tree is obtained by calculating the balance factor of a tree.

• Definition of Balance Factor

The balance factor BF(T) of a node in binary tree is defined to be h_L - h_R where he h_L and h_R are heights of left and right subtrees of T.

For any node in AVL tree the balance factor i.e. BF(T) is -1, 0 or +1

• Height of AVL tree

Theorem: The height of AVL tree with n elements (nodes) is O(logN).

Proof: Let an AVL tree with N nodes in it. Nh be the minimum number of nodes in an AVL tree of height h.

In worst case, one subtree may have height h-1 and other subtree may have height h−2. And both these subtrees are AVL trees. Since for every node in AVL tree the height of left and right subtrees differ by at most 1. Hence,

N_h = N_{h_1}+N_{h_2}+1

Where N_h denotes the minimum number of nodes in an AVL tree of height h.

N₀=0         N₁ =2

We can also write it as

N> N_h = N_h−2 + N_{h_2}+1

  > 2N_h-2

  > 4N_h-4

 .

.

.

 > 2ⁱ N_h-2i

If value of h is even, let i = h/2-1

Then equation becomes,

N > 2^h/2-1 N₂

= N > 2^h/2-1x4    N₂ =4

= O (log N)

If value of h is odd, let i= (h-1)/2 then equation becomes.

N > 2^(h-1)/2Nı

= N > 2^(h-1)/2x1    N1 =1

h=O(log N)

This proves that height of AVL tree is always O(log N). Hence search, insertion and deletion can be carried out in logarithmic time.

Theorem : The height of AVL tree h with minimum number of nodes n is 1.44 log n.

Proof ; Let F_h be the AVL tree with height h having minimum number of nodes. The tree can be shown as below.

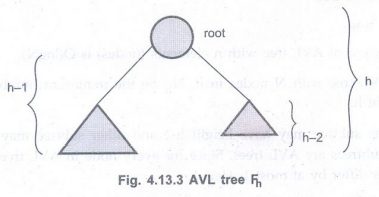
Hence minimum number of nodes in AVL tree is = Length of left subtree + Length of right subtree + 1

|F_h| = |F_h-1| + | F_h-2| + 1

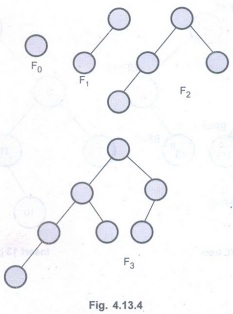
Also

|F₀|=1 and |F₁| = 2

This denotes the Fibonacci tree.

Adding 1 to both sides.

|F_h|+1=(|F_h-1|+1)+(|F_h-2|+1).

Thus the numbers | F_h|+1 are Fibonacci numbers. Using approximate formula for Fibonacci numbers, we will ge tan approximate value as :

|F_h|+1=1/√5 (1+√5/2) ^h+3

Taking logarithm

=h≈ 1.44 log | F_h |

Hence the worst case height of an AVL tree with n nodes is 1.44 log n.

The Fibonacci trees are as shown below.

Difference between AVL tree and binary search tree

Representation of AVL Tree

•The AVL tree follows the property of binary search tree. In fact AVL trees are basically binary search trees with balance factor as -1, 0 or + 1.

•After insertion of any node in an AVL tree if the balance factor of any node becomes other than -1, 0, or + 1 then it is said that AVL property is violated. Then we have to restore the destroyed balance condition. The balance factor is denoted at right top corner inside the node.

For example:

• After an insertion of a new node if balance condition gets destroyed, then the nodes on that path (new node insertion point to root) needs to be readjusted. That means only the affected subtree is to be rebalanced.

• The rebalancing should be such that entire tree should satisfy AVL property.

In above given example -

Insertion

There are four different cases when rebalancing is required after insertion of new node.

1. An insertion of new node into left subtree of left child (LL).

2. An insertion of new node into right subtree of left child (LR).

3. An insertion of new node into left subtree of right child (RL).

4. An insertion of new node into right subtree of right child (RR).

There is a symmetry between case 1 and 4. Similarly symmetry exists between case 2 and 3.

Some modifications done on AVL tree in order to rebalance it is called rotations of AVL tree.

There are two types of rotations.

Single rotation

Double rotation

Insertion algorithm

1. Insert a new node as new leaf just as in ordinary binary search tree.

2. Now trace the path from insertion point (new node inserted as leaf) towards root. For each node 'n' encountered, check if heights of left (n) and right (n) differ by at most 1.

a) If yes, move towards parent (n).

b) Otherwise restructure by doing either a single rotation or a double rotation.

Thus once we perform a rotation at node 'n' we do not require to perform any rotation at any ancestor on 'n'.

Different rotations in AVL tree

1. LL rotation

When node '1' gets inserted as a left child of node 'C' then AVL property gets destroyed i.e. node A has balance factor + 2.

The LL rotation has to be applied to rebalance the nodes.

2. RR rotation

When node '4' gets attached as right child of node 'C' then node 'A' gets  unbalanced. The rotation which needs to be applied is RR rotation as shown in Fig. 4.13.8.

When node '3' is attached as a right child of node 'C' then unbalancing occurs because of LR. Hence LR rotation needs to be applied.

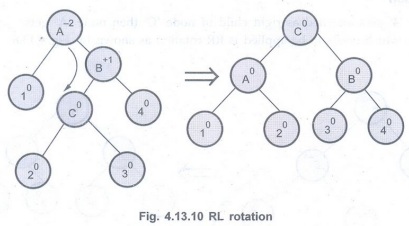
4. RL rotation

When node '2' is attached as a left child of node 'C' then node 'A' gets unbalanced as its balance factor becomes 2. Then RL rotation needs to be applied to rebalance the AVL tree.

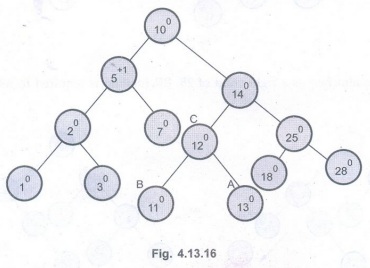
Example - Consider an AVL tree as given below.

We have to insert 1, 25, 28, 12 in this tree.

Insert 1

To insert node '1' we have to attach it as a left child of '2'. This will unbalance the tree as follows. We will apply LL rotation to preserve AVL property of it.

Insert 25

We will attach 25 as a right child of 18. No balancing is required as entire tree preserves the AVL property.

Insert 28

The node '28' is attached as a right child of 25. RR rotation is required to rebalance.

Now we will insert 12.

To rebalance the tree we have to apply LR rotation

Thus by applying various rotations depending upon direction of insertion of new node the AVL tree can be restructured.

Deletion

Even after deletion of any particular node from AVL tree, the tree has to be restructured in order to preserve AVL property. And thereby various rotations need to be applied.

Algorithm for deletion

The deletion algorithm is more complex than insertion algorithm.

1.Search the node which is to be deleted.

2. a) If the node to be deleted is a leaf node then simply make it NULL to remove.

    b) If the node to be deleted is not a leaf node i.e. node may have one or two children, then the node must be swapped with its inorder successor. Once the node is swapped, we can remove this node.

3. Now we have to traverse back up the path towards root, checking the balance factor of every node along the path. If we encounter unbalancing in some subtree then balance that subtree using appropriate single or double rotations.

The deletion algorithm takes O(log n) time to delete any node

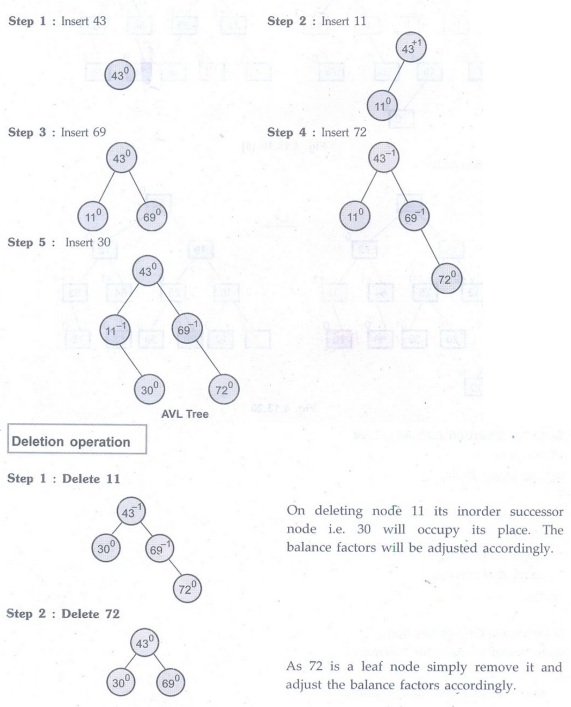
Consider an AVL

Thus the node 14 gets deleted from AVL tree.

4.13.4 Searching

The searching of a node in an AVL tree is very simple. As AVL tree is basically binary search tree, the algorithm used for searching a node from binary search tree is the same one is used to search a node from AVL tree.

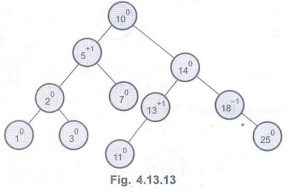
For example: Consider an AVL tree, as given below

Now if we want to search node with value 13 then, we will start searching process from root.

Step 1: Compare 13 with root node 10. As 13 > 10, search right subbranch.

Step 2: Compare 13 with 18. As 13 < 18, search left subbranch.

Step 3: Compare 13 with 12. As 13 > 12, search right subbranch.

Step 4: Compare 13 with 13. Declare now "node is found".

The searching operation takes O (log n) time.

The main objective here is to keep the tree balanced all the times. Such balancing causes the depth of the tree to remain at its minimum and therefore overall costs of search is reduced.

Ex. 4.13.1: Show the result of inserting 2, 1, 4, 5, 9, 3, 6, 7 into an empty AVL tree.

Sol. :

Ex. 4.13.2 Draw the result of inserting 20, 10 and 24 one by one into the AVL tree given below. Draw the tree after each insertion.

Sol. :

Step 1: Insertion of 20

Ex. 4.13.3: Show the results of inserting 43, 11, 69, 72 and 30 into an initally empty AVL tree. Show the results of deleting the nodes 11 and 72 one after the other of constructed tree.

Sol. Insertion operation

Ex. 4.13.4: Construct an AVL tree with the values 3,1,4,5,9,2,8,7,0 into an initially empty tree. Write code for inserting into AVL tree.

Sol.

Code for Insertion into AVL Tree

//Tree node

typedef struct Node

{

int data;

int BF;

struct Node *left;

struct Node *right;

}node;

// Definiton of insert function

node *insert(int data, int *current)

{

root = create(root, data, current);

return root;

}

//definition of create function

node *create(struct Node *root, int data, int *current)

{

node *temp1, *temp2;

if (root == NULL)//initial node

{

root = new node;

root->data = = data;

root->left = NULL;

root->right = NULL;

root->BF = 0;

*current = TRUE;

return(root);

}

if (data<root->data)

{

root->left = create(root->left, data, current);

// adjusting left subtree

if (*current)

{

switch (root->BF)

{

case 1:temp1 root->left;

if (temp1->BF ==1)

{

printf("\n single rotation: LL rotation");

root->left = temp1->right;

temp1->right = root;

root->BF = 0;

root = temp1;

}

else

{

printf("\n Double rotation:LR rotation");

temp2=temp1->right;

temp1->right = temp2->left;

temp2->left=temp1;

root->left = temp2->right;

temp2->right = root;

if (temp2->BF == -1)

root->BF = -1;

else

root->BF = 0;

if (temp2->BF == -1)

temp1->BF = 1;

else

temp1->BF = 0;

root = temp2;

}

root->BF = :0;

* current = FALSE;

break;

case 0:

root->BF = 1;

break;

case 1:

root->BF = 0;

*current = FALSE;

}//end of switch

}//inner if

}//outer if

if (data > root -> data)

{

root->right=create(root->right, data, current);

//adjusting the right subtree

if (*current != NULL)

{

switch (root->BF)

{

case 1:

root->BF = 0;

*current = FALSE;

break;

case 0:

root->BF = -1;

break;

case-1:

temp1 = root->right;

if (temp1->BF == -1)

{

printf("\n single rotation:RR rotation");

root->right = temp1->left;

temp1->left = root;

root->BF = 0;

root = temp1;

}

else

{

printf("\n Double rotation:RL rotation");

temp2 = temp1->left;

temp1->left = temp2->right;

temp2->right = temp1;

root->right temp2->left;

temp2->left = root;

if (temp2->BF == -1)

root->BF = 1;

else

root->BF = 0;

if (temp2->BF == 1)

temp1->BF = -1;

else

temp1->BF = 0;

root =temp2;

}

root->BF = 0;

* current = FALSE;

}

}

}

return(root);

}

void main()

{

node *root = NULL;

int current;

//calling insert function by passing values

root = insert(40, &current);

root = insert(50, &current);

root = insert(70, &current);

….

}

Ex. 4.13.5 Define AVL Tree and starting with an empty AVL search following elements in the given order 35, 45, 65, 55,75,15, 25.

Sol. AVL Tree Refer section 4.13.

Ex. 4.13.6: Write a routine for AVL tree insertion. Insert the following elements in the empty tree and how do you balance the tree after each element insertion Elements: 2, 5, 4, 6, 7, 9, 8, 3, 1, 10

Sol. :

Ex. 4.13.7: Implementation of AVL tree.

Sol. :

/**************************************************************

This program performs the insertion and deletion operations on an AVL tree

**************************************************************/

#include<stdio.h>

#include<stdlib.h>

#include<conio.h>

#define FALSE 0

#define TRUE 1

//Tree node

typedef struct Node

{

int data;

int BF;

struct Node *left;

struct Node *right;

}node;

node *insert(int data, int *current)

{

node *create(node *root,int data, int *current);

node *root;1

root=create(root,data,current);

return root;

}

node *remove(node *root,int data, int *current);

node *find_succ(node *temp,node *root, int *current);

node *right_rotation(node *root, int *current);

node *left_rotation(node *root, int *current);

void display(node *root);

node *create(struct Node *root,int data, int *current)

{

node *temp1,*temp2;

if(root == NULL)

{

root = new node;

root->data=data;

root->left=NULL;

root->right=NULL;

root->BF=0;

*current=TRUE;

return(root);

}

if(data<root->data)

{

root->left=create(root->left,data,current);

// adjusting left subtree

if(*current)

{

switch(root->BF)

{

case 1:temp1= root->left;

if(temp1->BF==1)

{

printf("\n single rotation: LL rotation");

root->left=temp1->right;

temp1->right=root;

root->BF=0;

root=temp1;

}

else

{

printf("\n Double roation:LR rotation");

temp2=temp1->right;

temp1->right=temp2->left;

temp2->left=temp1;

root->left=temp2->right;

temp2->right=root;

if(temp2->BF==1)

root->BF=-1;

else

root->BF=0;

if(temp2->BF==-1)

temp1->BF=1;

else

temp1->BF=0;

root=temp2;

}

root->BF=0;

*current=FALSE;

break;

case 0:

root->BF=1;

break;

case -1:

root->BF=0;

*current=FALSE;

}

}

}

if(data> root->data)

{

root->right=create(root->right,data,current);

//adjusting the right subtree

if(*current!= NULL)

{

case 1:                                           

root->BF=0;

*current=FALSE;

break;

case 0:

root->BF=-1;

break;

case -1:

temp1=root->right;

if(temp1->BF==-1)

{

printf("\n single rotation:RR rotation")

root->right=temp1->left;

temp1->left=root;

root->BF=0;

root=temp1;

}

else

{

printf("\n Double rotation:RL rotation");

temp2=temp1->left;

temp1->left=temp2->right;

temp2->right=temp1;

root->right=temp2->>left;

temp2->left=root;

if(temp2->BF==-1)

root->BF=1;

else

root->BF=0;

if(temp2->BF==1)

temp1->BF=-1;

else

temp1->BF=0;

root=temp2;

}

root->BF=0; *

current=FALSE;

}

}

}

return(root);

}

/*

Display of Tree in inorder fashion

*/

void display(node *root)

{

if(root!= NULL)

{

display(root->left);

printf("%d",root->data);

 display(root->right);

}

}

/*

Deletion of desired node the tree

*/

node *remove(node *root,int data, int *current)

{

node *temp;

if(root->data==13)

printf("%d",root->data);

if(root == NULL)

{

printf("\n Empty Tree!!!");

return (root);

}

else

{

if(data<root->data)

{

root->left=remove(root->left,data,current);

if(*current)

root=right_rotation(root,current);

}

else

{

if(data>root->data)

root->right-remove(root->right,data,current);

if(*current)

root-left_rotation(root, current);

}

else

{

temp=root;

if(temp->right== NULL)

{

root=temp->left;

*current=TRUE;

delete(temp);

}

else

{

if(temp->left== NULL)

{

root=temp->right;

* current=TRUE;

delete(temp);

}

else

{

temp->right=find_succ(temp->right,temp, current);

if(*current)

root=left_rotation(root,current);

}

}

}

}

}

return (root);

}

node *find_succ(node *succ,node *temp,int *current)

{

node *temp1=succ;

if(succ->left!= NULL)

{

succ->left=find_succ(succ->left,temp,current);

if(*current)

succ=right_rotation(succ,current);

}

else

{

temp1=succ;

temp->data=succ->data;

succ succ->right;

delete temp1;

*current=TRUE;

}

return (succ);

}

node *right_rotation(node *root, int *current)

{

node *temp1,*temp2;

switch(root->BF)

{

case 1:

root->BF=0;

break;

case 0:

root->BF -1;

*current=FALSE;

break;

case -1:

temp1=root->right;

if(temp1->BF<=0)

{

printf("\n single rotation: RR rotation");

root->right=temp1->left;

temp1->left=root;

if(temp1->BF==0)

{

root->BF=-1;

temp1->BF=1;

*current=FALSE;

}

else

{

root->BF=temp1->BF=0

}

root=temp1;

}

else

{

printf("\n Double Rotation:RL rotation");

temp2=temp1->left;

temp1->left=temp2->right;

temp2->right=temp1;

root->right=temp2->left;

temp2->left=root;

if(temp2->BF==-1)

root->BF=1;

else

root->BF=0;

if(temp2->BF==1)

temp1->BF=-1;

else

temp1->BF=0;

root=temp2;

temp2->BF=0;

}

}

return (root);

}

node *left_rotation(node *root,int *current)

{

node *temp1,*temp2;

switch(root->BF)

{

case 1:

root->BF=0;

break;

Case 0:

root->BF=1;

*current=FALSE;

break;

Case 1:

temp1=root->left;

if(temp1->BF>=0)

{

printf("\nsingle rotation LL rotation");

root->left=temp1->right;

temp1->right=root;

if(temp1->BF==0)

{

root->BF=1;

temp1->BF=-1;

*current=FALSE;

}

else

{

root->BF=temp1->BF=0;

}

root=temp1;

}

else

{

printf("\nDouble rotation:LR rotation");

temp2=temp1->right;

temp1->right-temp2->left;

temp2->left=temp1;

root->left=temp2->right;

temp2->right=root;

if(temp2->BF==1)

root->BF=-1;

else

root->BF=0;

if(temp2->BF==-1)

temp1->BF=1;

else

temp1->BF=0;

root=temp2;

temp2->BF=0;

}

}

return root;

}

void main()

{

node *root=NULL;

int current;

clrscr();

root=insert(40,&current);

root=insert(50,&current);

root=insert(70,&current);

printf("\n");

display(root);

printf("\n");

root=insert(30,&current);

printf("\n");

display(root);

root=insert(20,&current);

printf("\n");

display(root);

root=insert(45,&current);

printf("\n");

display(root);

root=insert(25,&current);

printf("\n");

display(root);

root=insert(10,&current);

printf("\n");

display(root);

root=insert(5,&current);

printf("\n");

display(root);

root=insert(22,&current);

printf("\n");

display(root);

root=insert(1, &current);

printf("\n");

display(root);

root=insert(35,&current);

printf("\n\nFinal AVL tree is: \n");

display(root);

printf("\n Removing node 20");

root remove(root,20,&current);

printf("\n Removing node 45");

root remove(root,45,&current);

printf("\n\n AVL tree after deletion of a node: \n");

display(root);

printf("\n");

}

Output

single rotation:RR rotation

40 50 70

30 40 50 70

single rotation: LL rotation

20 30 40 50 70

Double roation:LR rotation

20 30 40 45 50 70

Double roation:LR rotation

20 25 30 40 45 50 70

10 20 25 30 40 45 50 70

single rotation: LL rotation

5 10 20 25 30 40 45 50 70

Double roation:LR rotation

5 10 20 22 25 30 40 45 50 70

single rotation: LL rotation

1 5 10 20 22 25 30 40 45 50 70

Double roation:LR rotation

Final AVL tree is:

1 5 10 20 22 25 30 35 40 45 50 70

Removing node 20

single rotation LL rotation.

Removing node 45

AVL tree after deletion of a node:

1 5 10 22 25 30 35 40 50 70

Review Questions

1. Explain with illustration the various types of rotations needed to retain the properties of an AVL tree during insertion of a node. State the time complexity of insertion of a node into an AVL

2. Explain the following. routines in AVL tree with example. i) Insertion, ii) Delection, iii) Single rotation, iv) Double rotation. AU: May-14, Marks 16

3. Explain the AVL rotations with a suitable example.