Applications of Heap

Applications of Heap

Applications of Binary Heap

1. Binary heaps are useful data structures for sorting the elements using heapsort method.

2. Binary heaps are used to find the shortest path using Dijkstra's shortest path algorithm.

3. For finding k^th smallest element binary heaps are used.

Let us understand one of the application of binary heap and that is heap sort.

Heap Sort

Heap sort is a sorting method discovered by J. W. J. Williams. It works in two stages.

Heap sort-

 i) Heap construction

ii) Deletion of maximum key

1.     Heap construction: First construct a heap for given numbers.

2.      Deletion of maximum key: Delete root key always for (n 1) times to remaining heap. Hence we will get the elements in decreasing order. For an array implementation of heap, delete the element from heap and put the deleted element in the last position in array. Thus after deleting all the elements one by one, if we collect these deleted elements in an array starting from last index of array.

We get a list of elements in a ascending order.

ADT for heap sort

{

Instances: Heap is a tree data structure denoted by either a maxheap or minheap. Operations :

1. Create_heap(): This is the first task to be performed for sorting the elements using heap sort. The parent node must be either maximum of its children or minimum than its children. That means a maxheap or minheap should be constructed.

2. Swap(): The root node must be swapped with the node at the last position in tree.

3. Delete_node(): The node at the last position in the heap tree must be deleted.

4. Insert Q0: The deleted element from the heap must be inserted in the priority queue.

5. Delete_Q0: The element can be deleted from the priority queue by the front end, so that a sorted list can be obtained.

Ex. 4.16.1 :State algorithm to sort elements of a given array in ascending order using heap sort. Sort the following numbers using heap sort: 48, 0, -1, 82, 108, 72, 54.

Sol. Algorithm:

Step 1: Construct the max heap from given set of elements.

Step 2: Swap the root key with the last node key of the heap.

Step 3: Delete the last node and store its key at the end of the array.

Step 4: Heapify the remaining heap structure.

Step 5: Repeat step 2 to 4 until the last remaining node.

Step 6: Delete the last node and store it at the end of the array.

Step 7 Print all the elements of the array. This will display the elements in sorted order.

Consider, 48, 0, 1, 82, 108, 72, 54.

Stage I: Construct heap

We will construct max heap as follows -

Stage II: Delete root node and heapify repeatedly

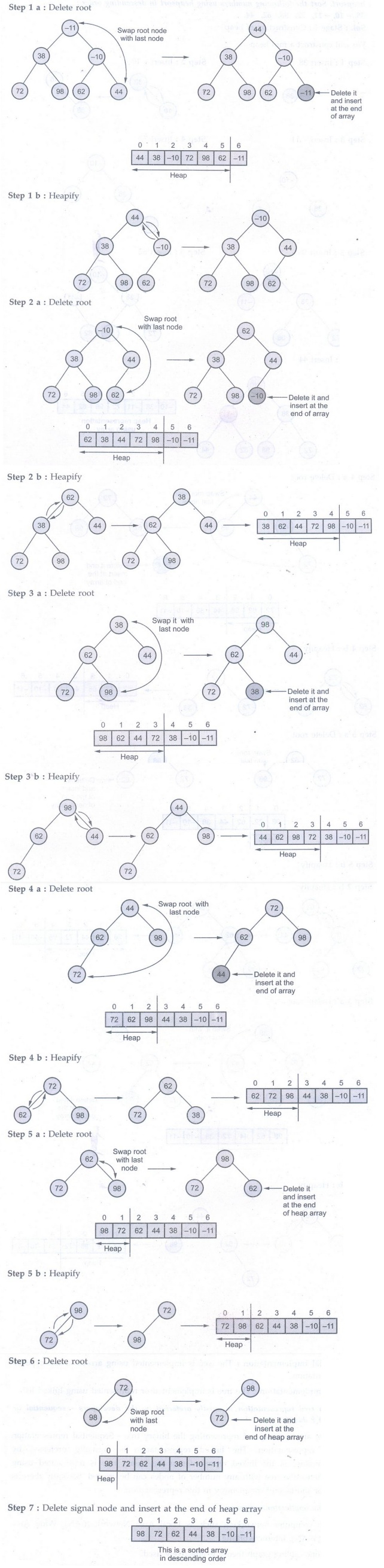
Ex. 4.16.2: State algorithm to sort elements of a given array in ascending order using heapsort. Sort the following numbers using heapsort in descending order: 38, 10, 11, 72, 98, 62, 44.

Sol. Stage I: Construction of heap

We will construct a min heap

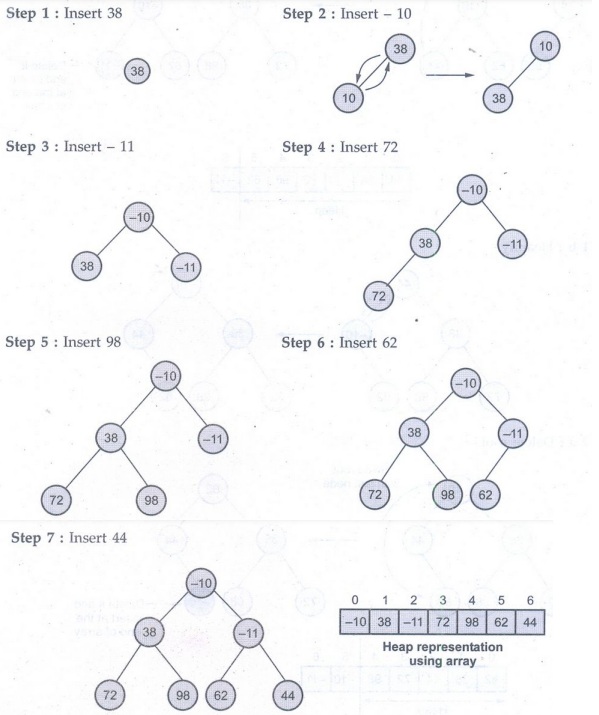
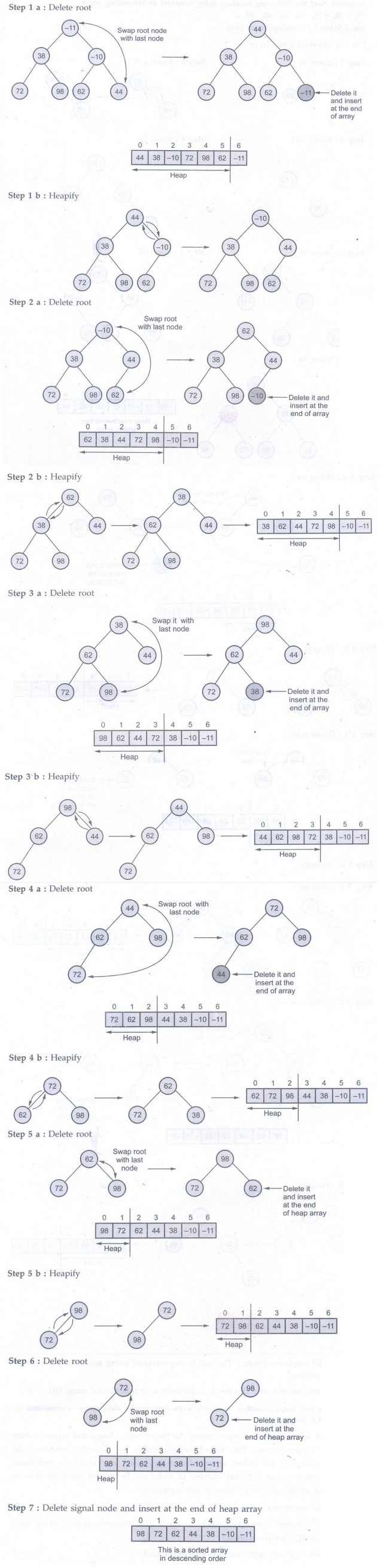
Stage II: Deletion of root node and hepify repeatedly.