Alpha-Beta Pruning

Alpha-Beta Pruning

AU: Dec.-04, 10, May-10, 17

Motivation for α – β Pruning

1. The problem with minimax algorithm search is that the number of game states it has to examine is exponential in the number of moves.

2. α- β proposes to compute the correct minimax algorithm decision without looking at every node in the game tree.

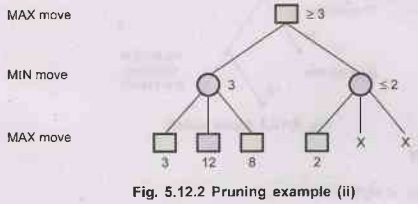
α-β Pruning Example :

Step 1:

Step 2:

Step 3:

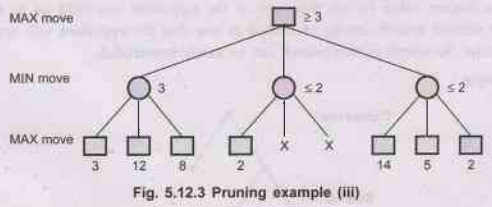
Steps in Alpha-Beta Pruning

1. MAX player cuts off search when he knows MIN-player can force a provably bad outcome.

2. MIN player cuts of search when he knows MAX-player can force provably good (for MAX) outcome.

3. Applying an alpha-cutoff means we stop search of a particular branch because we see that we already have a better opportunity elsewhere.

4. Applying beta-cutoff means we stop search of a particular branch because we see that the opponent already has a better opportunity elsewhere.

5. Applying both forms is alpha-beta pruning.

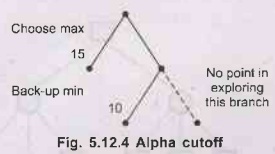
Alpha Cutoff

It may be found that, in the current branch, the opponent can achieve a state with a lower value for us than one achievable in another branch. So the current branch is one that we will certainly not move the game. Search of this branch can be safely terminated.

For example

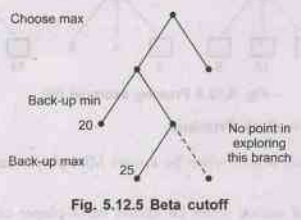
Beta-Cutoff

It is just the reverse of alpha-cutoff.

It may also be found, that in the current branch, we would be able to achieve a state which has a higher value for us than one of the opponent can hold us to in another branch. The current branch can be identified as one that the opponent will certainly not move the game. So search in this branch can be safely terminated.

For example -

Algorithm of Alpha-Beta Pruning

/*

alpha is the best score for max along the path to state.

beta is the beta is the best score for min along the path to state.

*/

If the level is the top level, let alpha= - infinity, beta = + infinity.

If depth has reached the search limit apply static evaluation function to state and return result.

If player is max:

Until all of state's children are examined with ALPHA-BETA or until alpha is equal to or greater than beta:

Call ALPHA-BETA (child, min, depth + 1, alpha, beta);

note result

Compare the value reported with alpha; if reported value is larger reset alpha to the new value.

Report alpha

If player is min:

Until all of state's children are examined with ALPHA-BETA or until alpha is equal to or greater than beta:

Call ALPHA-BETA, (child, max, depth + 1, alpha, beta);

note result.

Compare the value reported with beta; if reported value is smaller, reset beta to the new value.

Report beta.

Example of Alpha-Beta Pruning (Upto 3rd Ply)

Example 1:

1. In a game tree, each node represents a board position where one of the player gets to choose a move.

2. For example, look at node C in Fig. 5.12.6, as well as look at its left child.

3. We realize that if the players reach node C, the minimizer can limit the utility to 2. But the maximizer can get utility 6 by going to node B instead, so he would never let the game reach C. reach C. Therefore we don't even have to look at C's other children.

4. Initially at the root of the tree there is no gurantee about what values the maximizer and minimizer can achieve. So beta is set to ∞ and alpha to – ∞.

5. Then as we move down the tree, each node starts with beta and alpha values passed down from its parent.

6. If it's a maximizer node, then alpha is increased if a child value is greater than the current alpha value. Similarly, at a minimizer node, beta may be dereased. This procedure is shown in Fig. 5.12.6.

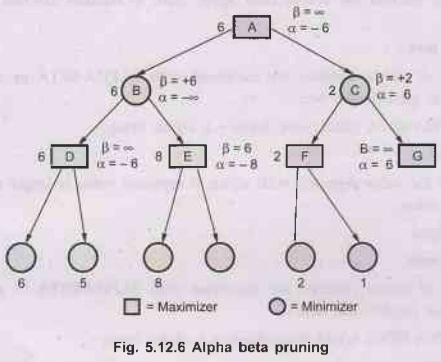
7. At each node, the alpha and beta values may be updated as we iterate over the node's children. At node E, when alpha is updated to a value of 8, it ends up exceeding beta.

8. This is a point where alpha-beta pruning is required we know the minimizer would never let the game reach this node, so we don't have to look at its remaining children.

9. In fact, pruning happens exactly when alpha becomes greater than or equal to beta - that is, when the alpha and beta lines hit each other in the node value.

Example 2: Explain Alpha-beta cut-offs in game playing with example.

1) Alpha-beta cut-offs is a modified version of minimax algorithm, wherein two threshold values are maintained for future expansion.

2) One representing a lower bound on the value that a maximizing node ultimately, be assigned (we call this alpha) and another representing a upper bound on the value that a minimizing node may be assigned (this we call beta).

3) To explain how alpha-beta values help, consider the tree structure in Fig. 5.12.7.

• Here, the maximizer has to play followed by the minimizer. As is done in minimax, look ahead search is done.

• The maximizer assigns a value 9 at B (minimum of the value at D and E). This value is passed back to A. So the maximizer is assured to have a value greater than 9. When it moves to B.

• Now, consider the case of node C. Value at node F is 5, and at G is unknown.

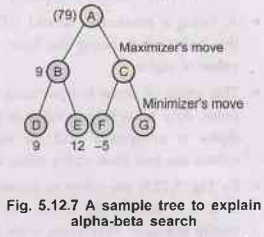
• Since, the move is a minimizing one, by moving to C, A can get value - 2 or less than that. This is totally unacceptable to A because by moving to B, he is assured to have a value equal to 6 or greater than this.

• So, by simply pruning the tree whose root is G, one saves a lot of time in searching.

4) Now effects of alpha and beta could be understood by Fig. 5.12.8. Here, a look ahead search is done upto a level 3 as shown in Fig. 5.12.8. The static evaluation function generator has assigned values which are given for the leaf nodes. Since, D, E, F and G are maximizers, the maximum of leaf nodes are assigned to them. Thus D, E, F and G has value 8, 10, 5 and 11.

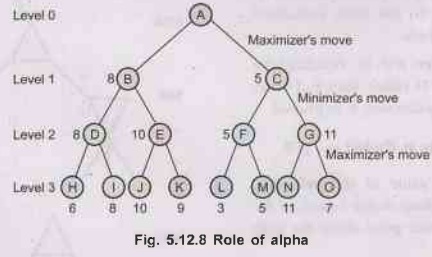
5) Here B and C are minimizers, so they are assigned a value minimum of their successors i.e., B is assigned a value 8 and C is assigned a value 5. And A is maximizer so A will obviously opt a value 8.

• ROLE OF ALPHA - For A, the maximizer, a value of 8 is assured by moving to node B. This value is compared with that of the value at C.

• A, being a maximizer would follow a path whose value is greater than 8. Hence, this value of 8, being the least that a maximizing node can obtain is set as the value of alpha.

• This value of alpha is now used as reference point. Any node whose value is greater than alpha is acceptable and all nodes whose values are less than alpha value are rejected. By Fig. 5.12.8, we come to know, that value at C is 5. Hence, the entire tree under B is totally rejected. That saves a lot of time and cost.

• ROLE OF BETA - Now, to know the role of BETA consider Fig. 5.12.9.

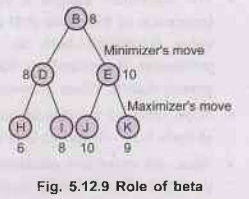
Here, B is root, B is minimizer and the paths for expansion are chosen from the values at each leaf nodes.

Since, D and E are maximizer's the maximum values of their children are backed up as their static evaluation function values. Node B being, a minimizer will always move to D rather than E. The value at D(8) is now used by B as a reference. This value is called beta, the maximum value, a minimizer can be assigned. Any node whose value is less than this beta value (8) is acceptable and values more than beta are seldom referred. The value of beta is passed to node E. Comparing it with the static evaluation function value there.

The minimizer will be benefited by only moving to D rather than E. Hence, the entire tree under note E is pruned.

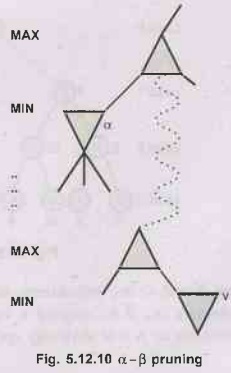
Why is it Called α-β?

• α is the value of the best (i.e., highest-value) choice found so far at any choice point along the path for max.

• If γ is worse than a (as shown in A diagram), max will avoid it.

• Similarly ẞ can be defined for min.

Heuristic Function that can be used in Cutting Off Search

1. Evaluation Functions

1. An evaluation function returns an estimate of the expected utility of the game from a given position, just as the heuristic functions return an estimate of the distance to the goal.

2. It should be clear that the performance of a game-playing program is dependant on quality of its evaluation function. An inaccurate evaluation function will guide an agent toward positions that turn out to be lost.

3. Designing evaluation Function:

a) The evaluation function should order the terminal states in the same way as the true utility function; otherwise, an agent using it might select sub optimal moves even if it can see ahead all the way to the end of the game.

b) The computation must not take too long!

c) For non terminal states, the evaluation function should be strongly correlated with the actual chances of winning.

2. Imperfect and Real-time Decisions

The minimax algorithm generates the entire game search space, whereas the alpha-beta algorithm allow us to prune large parts of it. However, alpha-beta still has to search all the way to terminal states for at least a portion of the search space. This depth is usually not practical, because moves must be made in a reasonable amount of time-typically a few minutes at most.

For making search faster we can make a heuristic evaluation function that can be applied to states in the search. It will effectively turn nonterminal nodes into terminal leaves. In other words, the suggestion is to alter minimax or alpha-beta in two ways; the utility function is replaced by a heuristic evaluation function, which gives an estimate of the positions utility, and the terminal test is replaced by a cutoff test that decides when to apply heuristic function.

3. Cutting Off Search

1. Cutting off search is simple approach for searching faster.

2. The cutting off search is applied to limit the depth.

If Cutoff-Test (s, depth) then return E(S) problem in cutting off search. (Where E is evaluation function).

3. Cutoff test might be applied in adverse condition.

4. It may stop search before allowable time.

5. Iterative deepening go until time is elapsed.

6. Quiescent position -

a) If a position looks "dynamic", don't even bother to evaluate it.

b) Instead, do a small secondary search until things calm down. For example -After capturing a piece, things look good, but this would be misleading if opponent was about to capture, right back.

c) In general such factors are called continuation heuristics.

d) A quiescent position is a position which is unlikely to exhibit wild swings (huge changes) in value in near future.

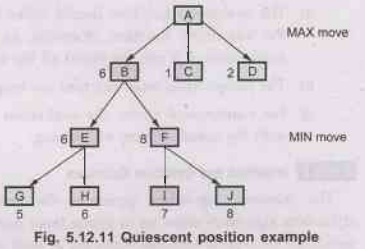
e) Consider following example –

Here [Refer Fig. 5.12.11] now since the tree is further explored, the values, which is passed to A, is 6. Thus the situation calms down. This is called as waiting for quiescence. This helps in avoiding the horizon effect of a drastic change of values.

7. The horizon effect -

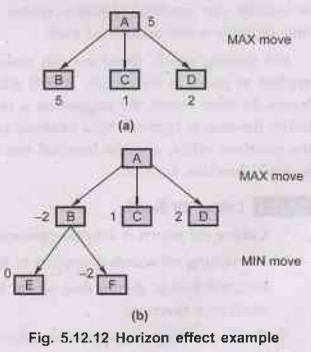
A potential problem that arises in game tree search (of a fixed depth) is the horizon effect, which occurs when there is a drastic change in value, immediately beyond the place where the algorithm stops searching. Consider the tree show in Fig. 5.12.12 (a).

It has nodes A, B, C and D. At this level since it is a maximizing ply, the value which will passed up at A is 5.

Suppose node B is examined one more level as shown in Fig. 5.12.12 (b), then we see that because of a minimizing ply, value at B is 2 and hence the value passed to A is 2. This results in a drastic change in the situation. There are two proposed solutions to this problem

a) Singular extension -

Which expands a move that is clearly better than all other moves. Its cost is higher with branching factor 1.

b) Secondary search-

One proposed solution is to examine the search space, beyond the apparently best one, to see that if something is looming just over the horizon. In that case we can revert to second-best move. Obviously then the second-best move has the same problem, and there isn't time to search beyond all possible acceptable moves.

8. Additional refinements - Other than alpha-beta pruning, there are a variety of other modifications to the minimax procedure that can also enhance its performance.

During searching, maintain two values alpha and beta so that alpha is the current lower bound of the possible returned value; beta is the current upper bound of the possible returned value. If during searching, we know for sure alpha > beta, then there is no need to search any more in this branch. The returned value cannot be in this branch. Backtrack until it is the case alpha beta. The two values alpha and beta are called the ranges of the current search window. These values are dynamic. Initially, alpha is - ∞ and beta is.

The quiescence and secondary search technique - If a node represents a state in the middle of an exchange of pieces, the evaluation function may not give a reliable estimate of board quality. For example, after a knight is captured, the evaluation may be good, but this is misleading as the opponent is about to capture one's queen.

The solution to this problem is, if node evaluation is not "quiescent", continue alpha-beta search can be made below that node but limit moves to those that significantly change evaluation function (for example, capture moves or promotions). The crucial complexity point is that branching factor for such moves is small.

For complicated games it is not feasible to select a move by simply looking-up the current game configuration in a catalogue (the book move) and extracting the current move. The catalogue would be huge and very complex for construction.

4. Forward Pruning

1. It is another method for searching faster.

2. In this, some moves at a given node are pruned immediately without further consideration. Clearly, most humans playing chess only consider a few moves from each position (at least consciously).

3. Unfortunately, the approach is rather dangerous because there is no guarantee that the best move will not be pruned away.

4. This can be disasterous if applied near the root, because it may happen that, often the program will miss some "obvious" moves.

5. Forward pruning can be used safely in special situations. For example, when two moves are symmetric or otherwise equivalent, only one of them need be considered or for nodes that are deep in the search tree.